Одновыборочный t-критерий используется для проверки того, равно ли среднее значение совокупности некоторому значению.
В этом руководстве объясняется, как провести один образец t-критерия в Excel.
Как провести одновыборочный t-тест в Excel
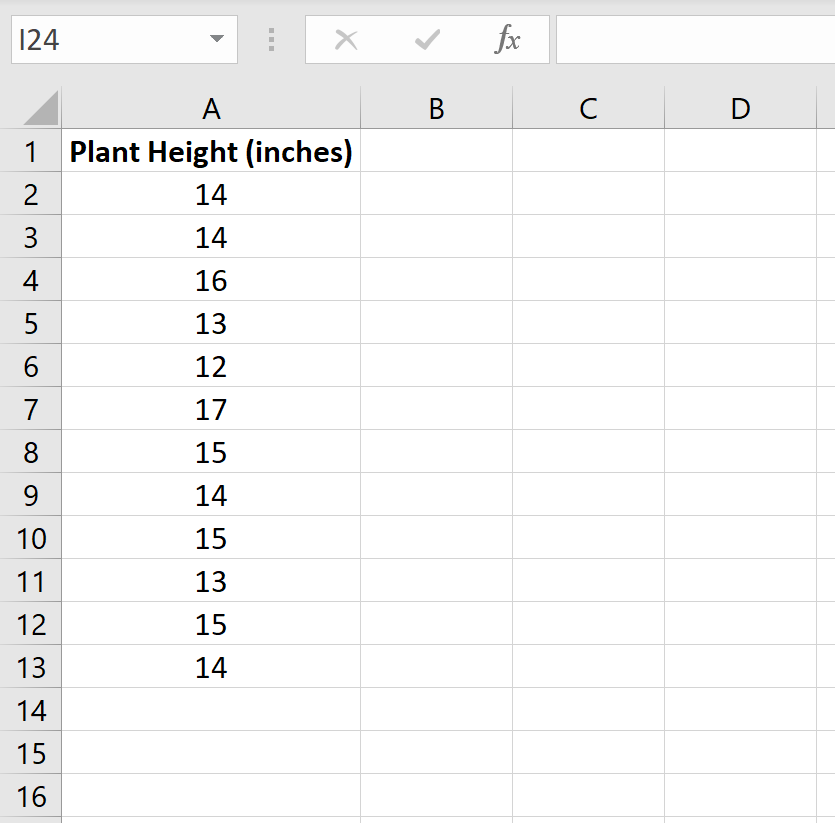
Предположим, ботаник хочет знать, равна ли средняя высота определенного вида растения 15 дюймам. Она собирает случайную выборку из 12 растений и записывает их высоту в дюймах.
На следующем изображении показана высота (в дюймах) каждого растения в образце:
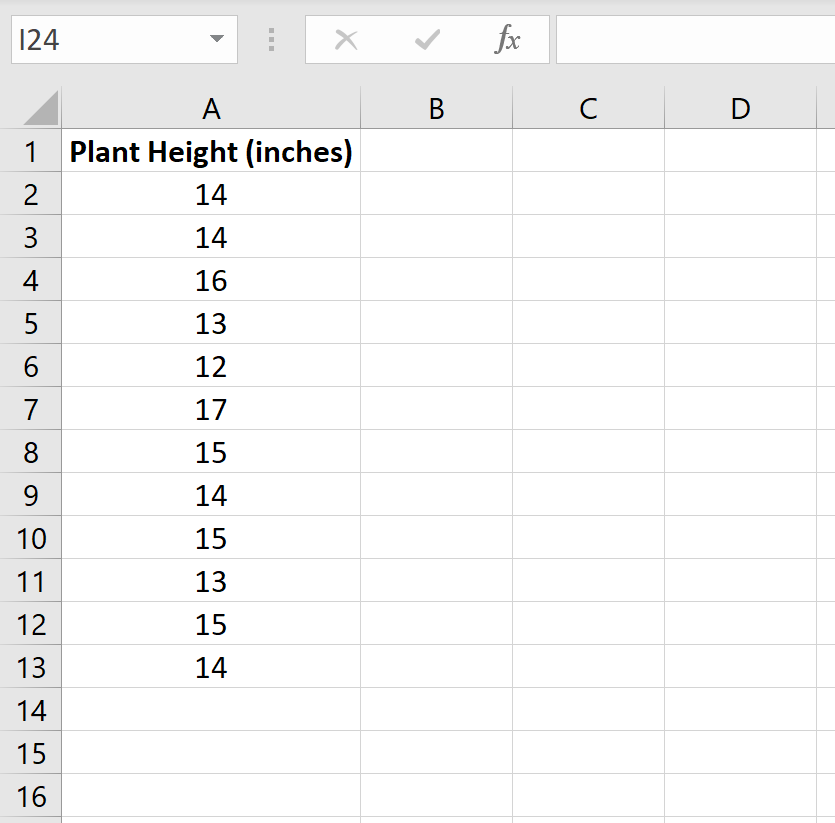
Мы можем использовать следующие шаги, чтобы провести t-тест для одной выборки, чтобы определить, действительно ли средняя высота для этого вида растений равна 15 дюймам.
Шаг 1: Найдите размер выборки, среднее значение выборки и стандартное отклонение выборки.
Во-первых, нам нужно найти размер выборки, среднее значение выборки и стандартное отклонение выборки, которые будут использоваться для проведения одновыборочного t-теста.
На следующем изображении показаны формулы, которые мы можем использовать для расчета этих значений:
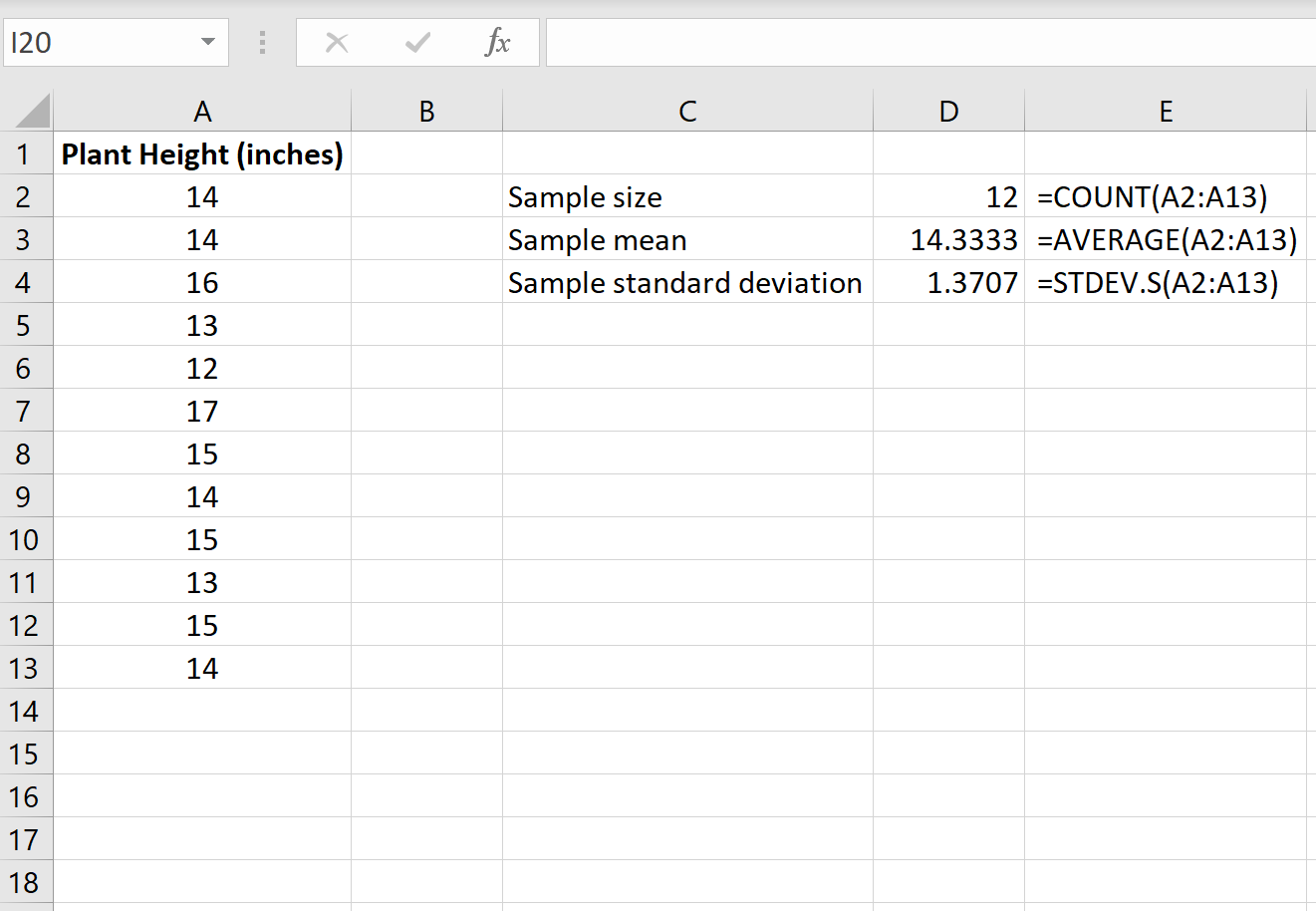
Шаг 2: Рассчитайте тестовую статистику t .
Далее мы рассчитаем тестовую статистику t по следующей формуле:
т = х - µ / (с / √ п )
куда:
x = выборочное среднее
µ = предполагаемое среднее значение населения
s = стандартное отклонение выборки
n = размер выборки
На следующем изображении показано, как рассчитать t в Excel:
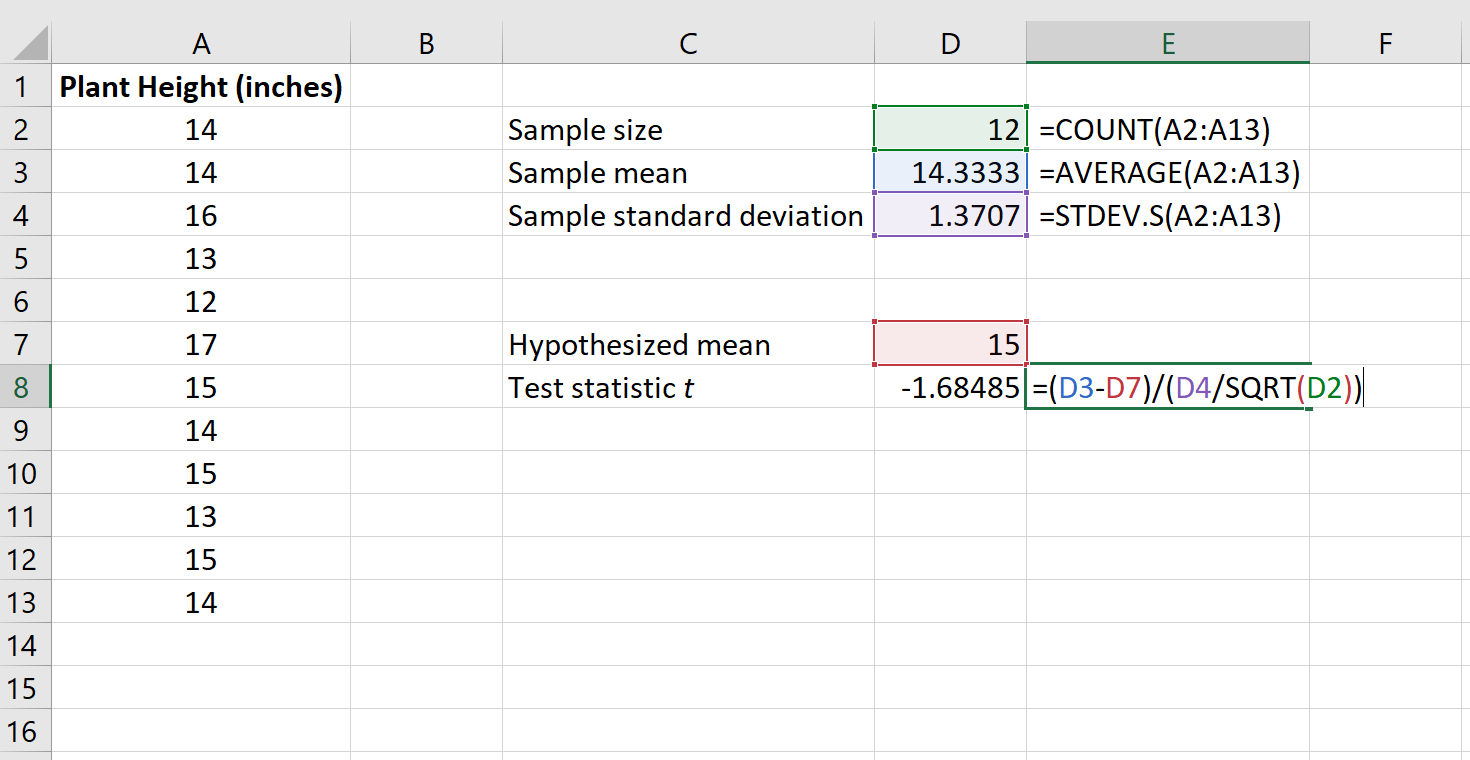
Тестовая статистика t оказывается равной -1,68485 .
Шаг 3: Рассчитайте p-значение тестовой статистики.
Затем нам нужно рассчитать значение p, связанное со статистикой теста, с помощью следующей функции в Excel:
=T.РАСП.2T(ABS(x), степень_свободы)
куда:
x = тестовая статистика t
deg_freedom = степени свободы для теста, которые рассчитываются как n-1
Технические примечания:
Функция T.DIST.2T() возвращает p-значение для двустороннего t-критерия. Если вместо этого вы проводите левосторонний t-критерий или правосторонний t-критерий, вы должны вместо этого использовать функции T.DIST() или T.DIST.RT() соответственно.
На следующем изображении показано, как рассчитать p-значение для нашей тестовой статистики:
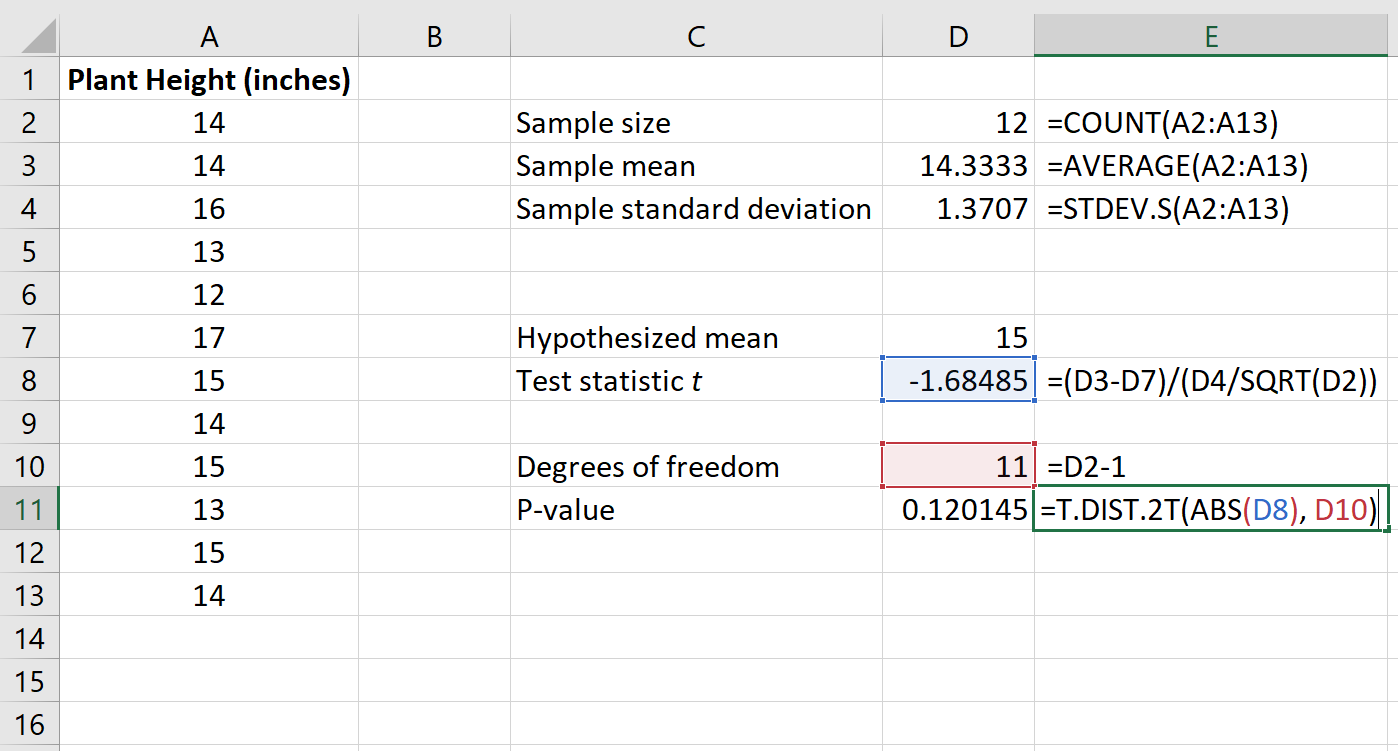
Значение p оказывается равным 0,120145 .
Шаг 4: Интерпретируйте результаты.
Две гипотезы для этого конкретного t-критерия с одной выборкой следующие:
H 0 : µ = 15 (средняя высота этого вида растений составляет 15 дюймов)
H A : µ ≠15 (средняя высота не 15 дюймов)
Поскольку p-значение нашего теста (0,120145) больше, чем альфа = 0,05, мы не можем отвергнуть нулевую гипотезу теста.
У нас нет достаточных доказательств, чтобы сказать, что средняя высота этого конкретного вида растений отличается от 15 дюймов.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные типы t-тестов в Excel.
Как провести двухвыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel