Стьюдентный критерий для парных выборок используется для сравнения средних значений двух выборок, когда каждое наблюдение в одной выборке может быть сопоставлено с наблюдением в другой выборке.
В этом руководстве объясняется, как провести t-критерий парных выборок в Excel.
Как провести t-тест для парных выборок в Excel
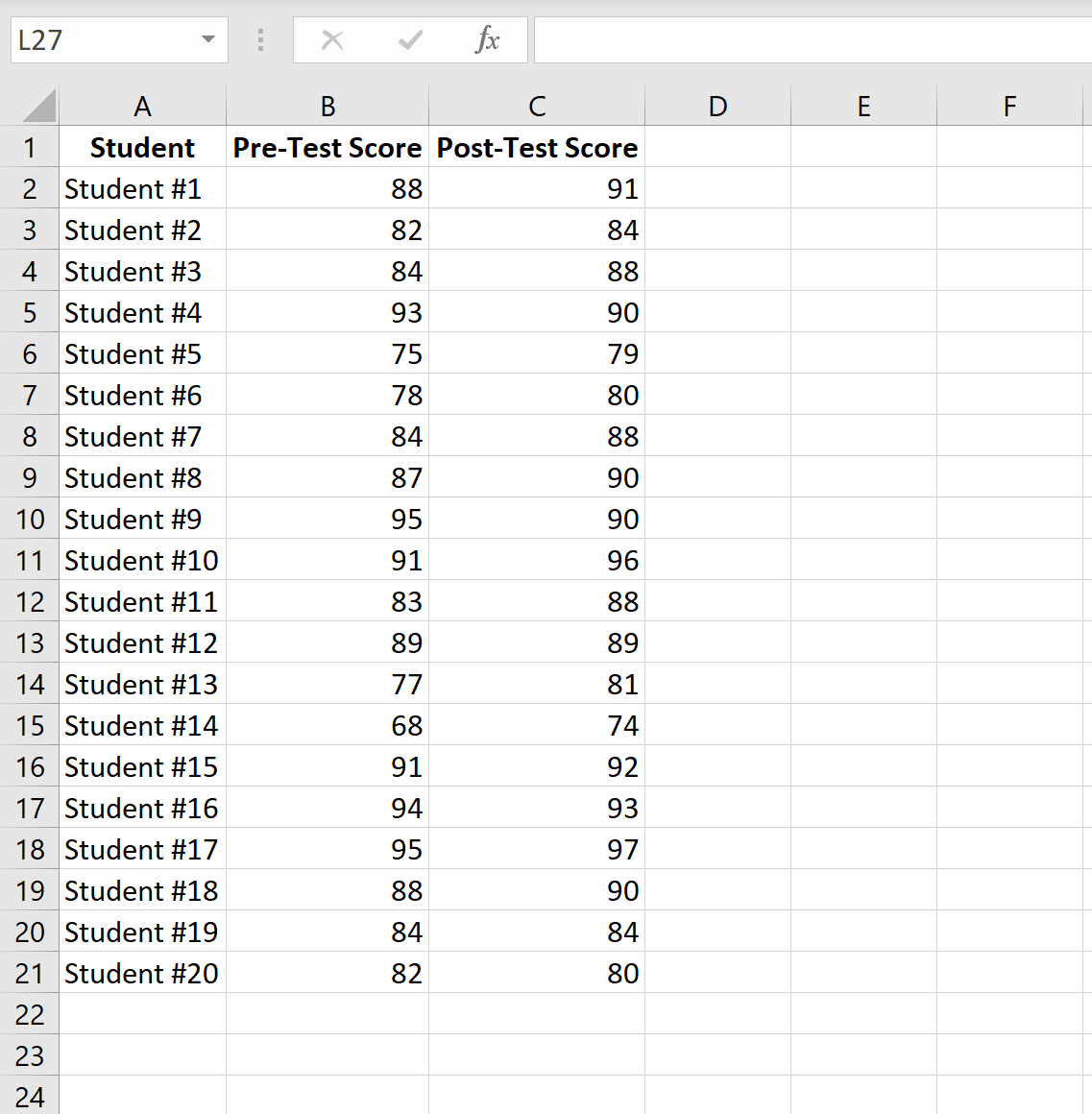
Предположим, мы хотим знать, значительно ли влияет определенная учебная программа на успеваемость студента на конкретном экзамене. Чтобы проверить это, у нас есть 20 учеников в классе, которые проходят предварительный тест. Затем каждый из студентов участвует в учебной программе в течение двух недель. Затем учащиеся пересдают тест аналогичной сложности.
Чтобы сравнить разницу между средними баллами по первому и второму тесту, мы используем t-критерий для парных выборок, потому что для каждого учащегося его балл за первый тест можно сопоставить с баллом за второй тест.
На следующем изображении показана оценка до теста и оценка после теста для каждого учащегося:
Выполните следующие шаги, чтобы провести t-критерий для парных выборок, чтобы определить, существует ли значительная разница в средних результатах теста между предварительным тестом и посттестом.
Шаг 1: Откройте пакет инструментов анализа данных.
На вкладке «Данные» на верхней ленте нажмите «Анализ данных».

Если вы не видите этот вариант для выбора, вам необходимо сначала загрузить пакет инструментов анализа , который является совершенно бесплатным.
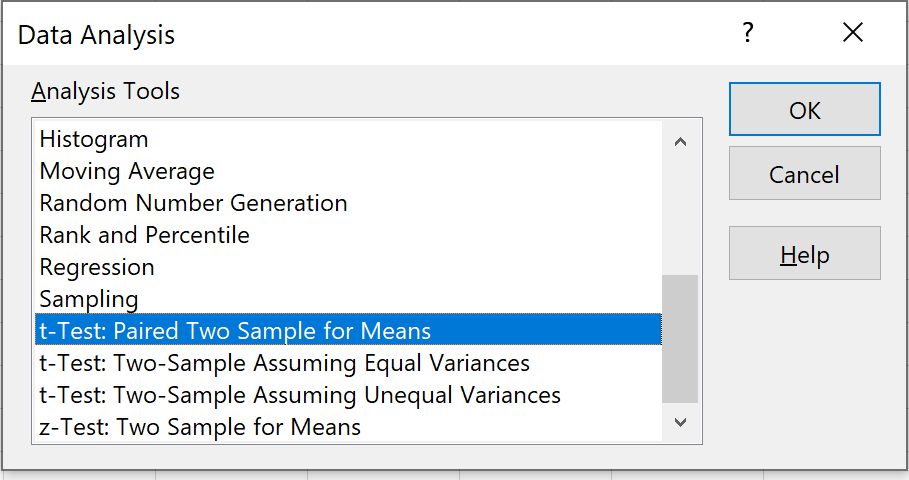
Шаг 2: Выберите подходящий тест для использования.
Выберите вариант с надписью t-Test: Paired Two Sample for Means и нажмите OK.
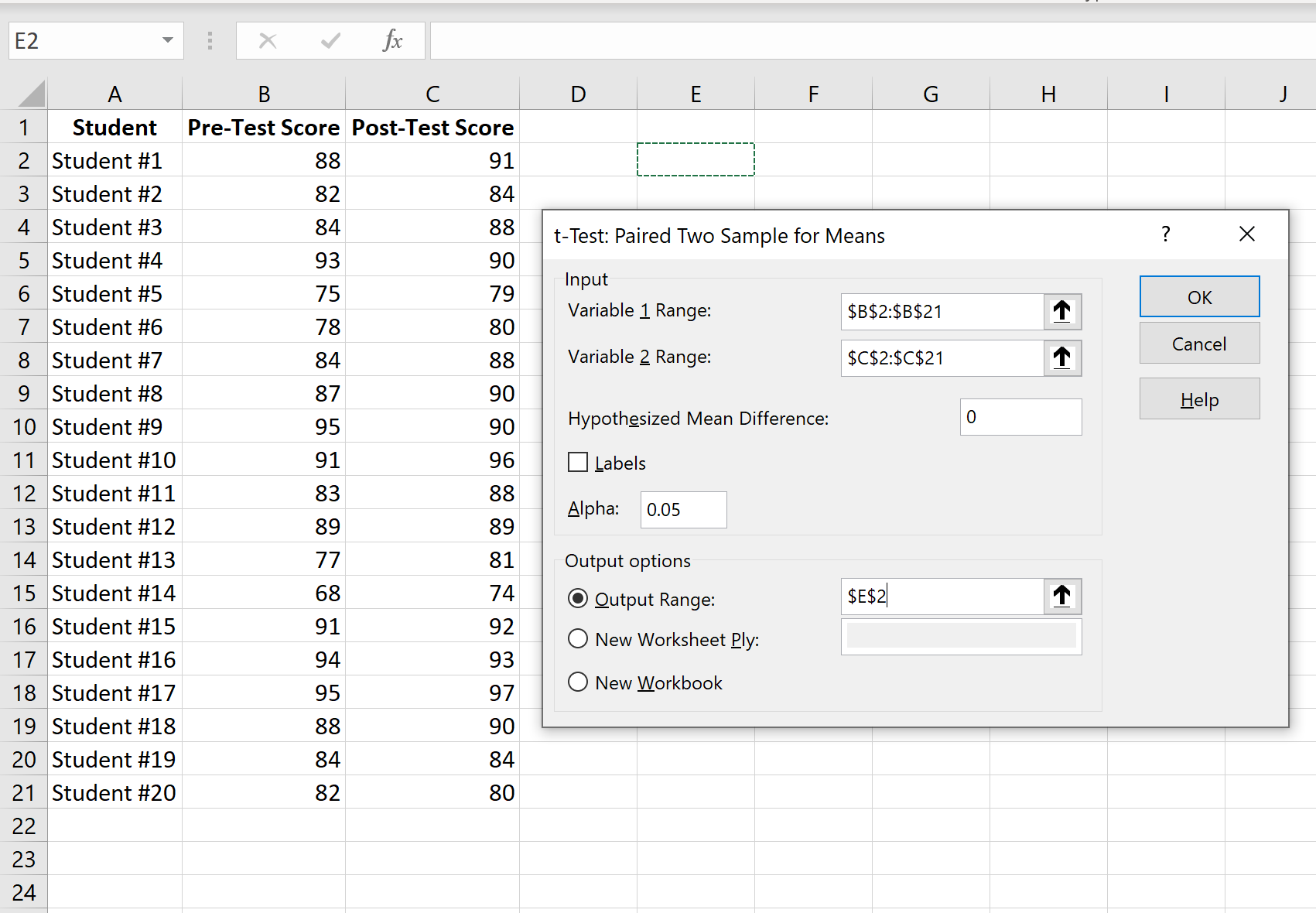
Шаг 3: Введите необходимую информацию.
Введите диапазон значений для Переменной 1 (оценки до теста), Переменной 2 (оценки после теста), гипотетической средней разницы (в этом случае мы поместили «0», потому что мы хотим знать, является ли истинная средняя разница между оценки до теста и оценки после теста равны 0), а выходной диапазон, в котором мы хотели бы видеть результаты теста, отображаются. Затем нажмите ОК.
Шаг 4: Интерпретируйте результаты.
После того, как вы нажмете OK на предыдущем шаге, отобразятся результаты t-теста.
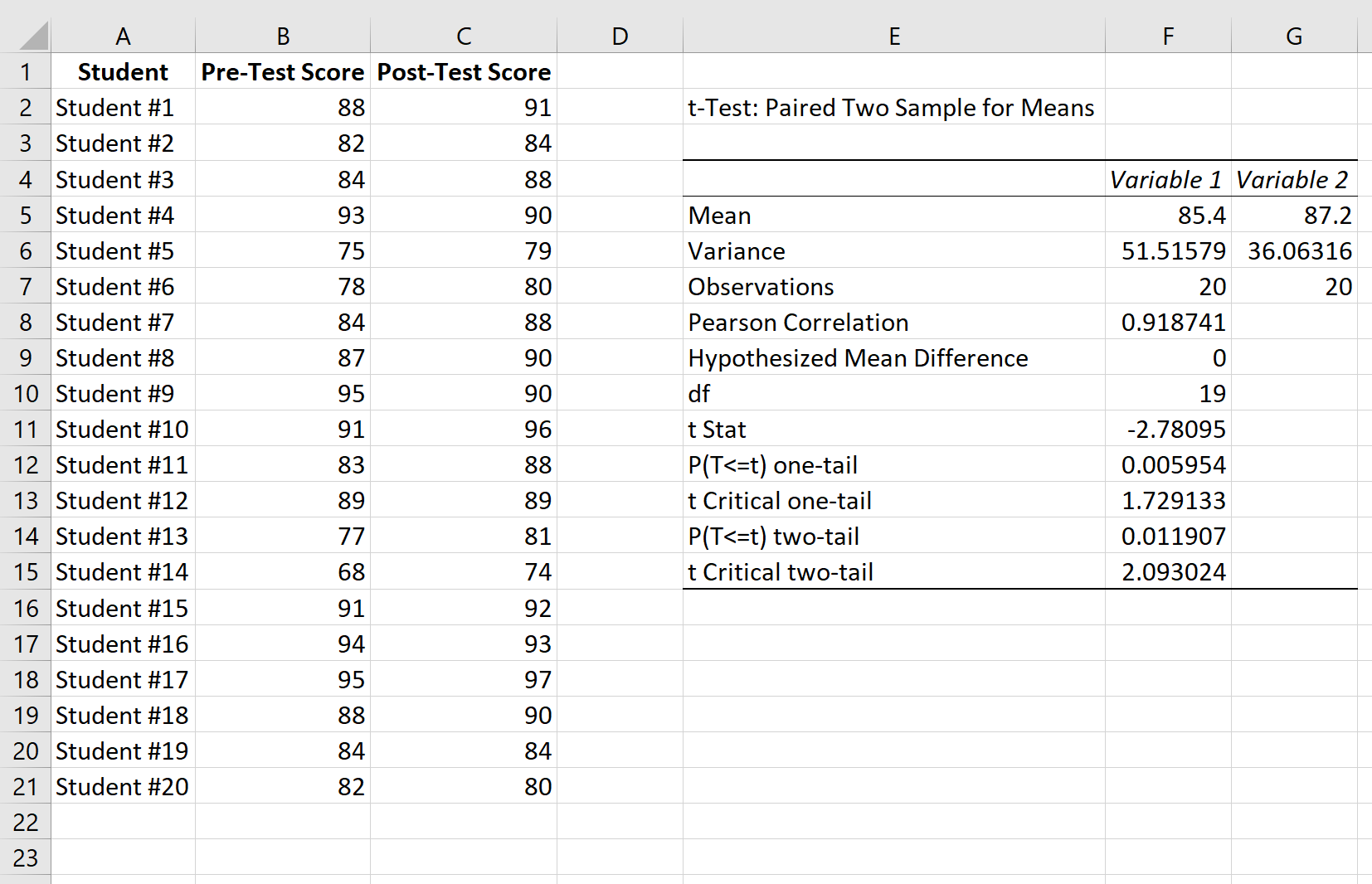
Вот как интерпретировать результаты:
Среднее значение: это среднее значение для каждого образца. Средний балл до теста — 85,4 , а средний балл после теста — 87,2 .
Дисперсия: это дисперсия для каждого образца. Дисперсия оценок до теста составляет 51,51 , а дисперсия оценок после теста — 36,06 .
Наблюдения: это количество наблюдений в каждой выборке. Обе выборки имеют по 20 наблюдений.
Корреляция Пирсона: корреляция между результатами до и после теста. Получается 0,918 .
Гипотетическая средняя разница: число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями. В данном случае мы выбрали 0 , потому что хотим проверить, есть ли вообще какая-либо разница между результатами до и после теста.
df: Степени свободы для t-критерия. Это рассчитывается как n-1, где n — количество пар. В этом случае df = 20 – 1 = 19 .
t Stat: тестовая статистика t , которая оказывается равной -2,78 .
P(T<=t) двухсторонний: значение p для двустороннего t-критерия. В этом случае р = 0,011907.Это меньше, чем альфа = 0,05, поэтому мы отвергаем нулевую гипотезу. У нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средним баллом до и после теста.
t Критический двухсторонний: это критическое значение теста, найденное путем определения значения в таблице распределения t , которое соответствует двустороннему тесту с альфа = 0,05 и df = 19. Получается 2,093024.Поскольку абсолютное значение нашей тестовой статистики t больше этого значения, мы отвергаем нулевую гипотезу. У нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средним баллом до и после теста.
Обратите внимание, что подход с использованием p-значения и критического значения приведет к одному и тому же выводу.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие t-тесты в Excel:
Как провести одновыборочный t-тест в Excel
Как провести двухвыборочный t-тест в Excel