В статистике мультиколлинеарность возникает, когда две или более переменных-предикторов сильно коррелируют друг с другом, так что они не предоставляют уникальную или независимую информацию в регрессионной модели.
Если степень корреляции между переменными достаточно высока, это может вызвать проблемы при подгонке и интерпретации регрессионной модели.
Самый крайний случай мультиколлинеарности известен как совершенная мультиколлинеарность.Это происходит, когда по крайней мере две переменные-предикторы имеют точную линейную связь между собой.
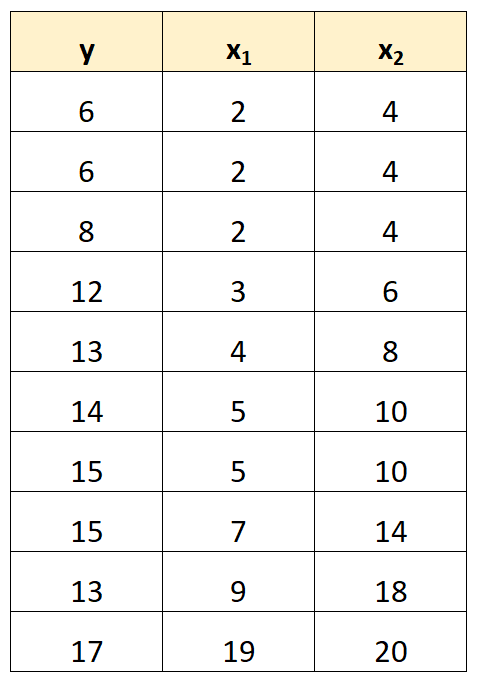
Например, предположим, что у нас есть следующий набор данных:
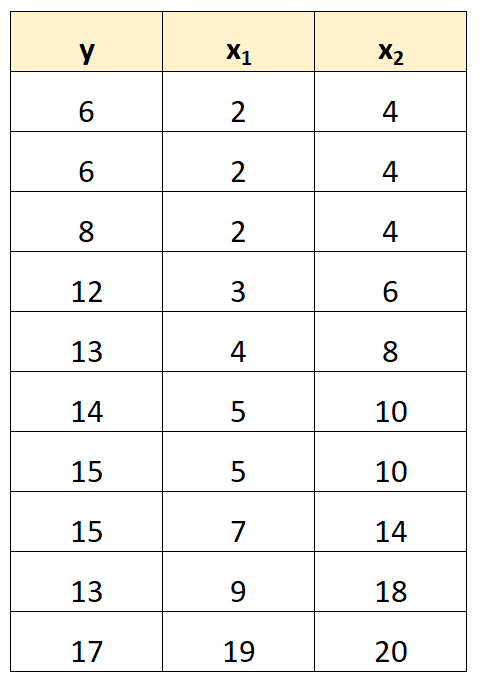
Обратите внимание, что значения переменной-предиктора x2 — это просто значения x1 , умноженные на 2 .
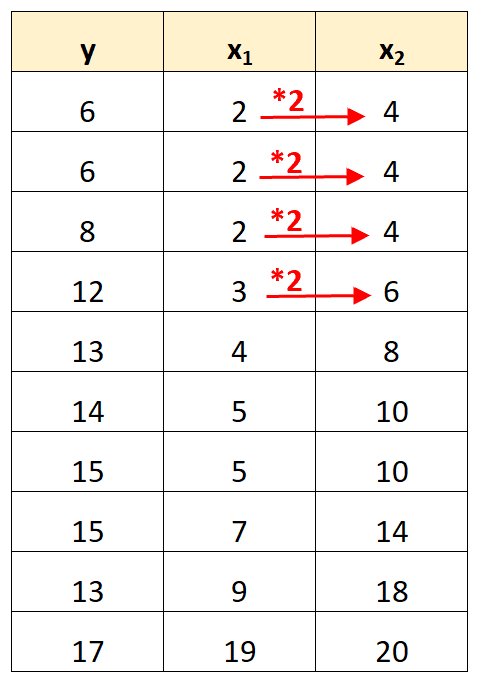
Это пример идеальной мультиколлинеарности .
Проблема с совершенной мультиколлинеарностью
Когда в наборе данных присутствует идеальная мультиколлинеарность, метод обычных наименьших квадратов не может дать оценки для коэффициентов регрессии.
Это связано с тем, что невозможно оценить предельное влияние одной переменной-предиктора (x 1 ) на переменную отклика (y), сохраняя постоянной другую переменную-предиктор (x 2 ), потому что x 2 всегда перемещается точно тогда, когда движется x 1 .
Короче говоря, идеальная мультиколлинеарность делает невозможным оценку значения каждого коэффициента в регрессионной модели.
Как справиться с идеальной мультиколлинеарностью
Самый простой способ справиться с идеальной мультиколлинеарностью — отбросить одну из переменных, которая имеет точную линейную связь с другой переменной.
Например, в нашем предыдущем наборе данных мы могли просто отбросить x 2 в качестве переменной-предиктора.
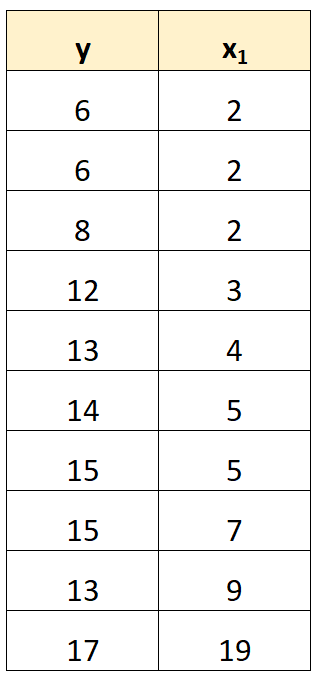
Затем мы подогнали бы модель регрессии, используя x 1 в качестве переменной-предиктора и y в качестве переменной отклика.
Примеры идеальной мультиколлинеарности
В следующих примерах показаны три наиболее распространенных сценария идеальной мультиколлинеарности на практике.
1. Одна предикторная переменная кратна другой
Предположим, мы хотим использовать «рост в сантиметрах» и «рост в метрах», чтобы предсказать вес определенного вида дельфинов.
Вот как может выглядеть наш набор данных:
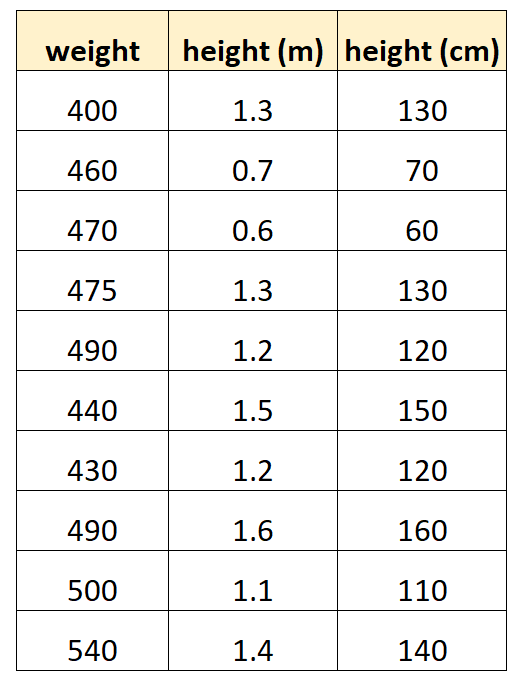
Обратите внимание, что значение «роста в сантиметрах» просто равно «росту в метрах», умноженному на 100. Это случай идеальной мультиколлинеарности.
Если мы попытаемся подогнать модель множественной линейной регрессии в R, используя этот набор данных, мы не сможем произвести оценку коэффициента для предикторной переменной «метры»:
#define data
df <- data.frame(weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))
#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)
#view summary of model
summary(model)
Call:
lm(formula = weight ~ m + cm, data = df)
Residuals:
Min 1Q Median 3Q Max
-70.501 -25.501 5.183 19.499 68.590
Coefficients: (1 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 458.676 53.403 8.589 2.61e-05 \*\*\*
m 9.096 43.473 0.209 0.839
cm NA NA NA NA
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395
2. Одна переменная-предиктор является преобразованной версией другой.
Предположим, мы хотим использовать «очки» и «масштабированные очки» для прогнозирования рейтинга баскетболистов.
Предположим, что переменная «масштабированные точки» рассчитывается как:
Баллы по шкале = (баллы – μ баллов ) / σ баллов
Вот как может выглядеть наш набор данных:
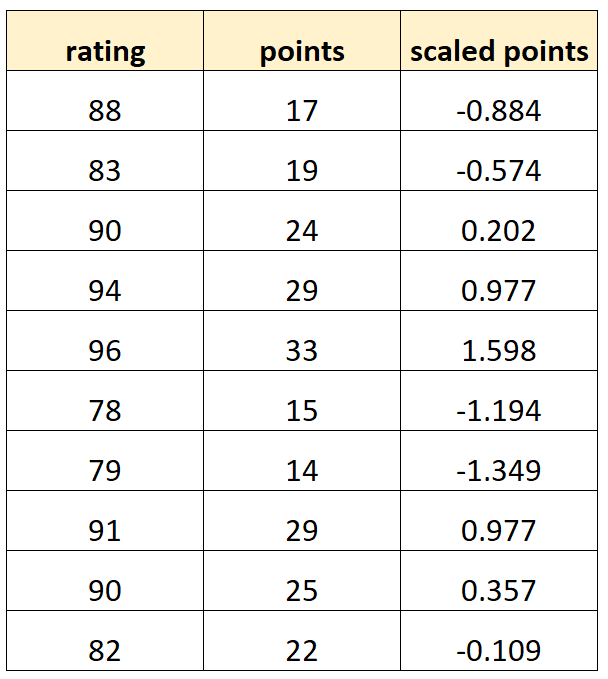
Обратите внимание, что каждое значение «масштабированных баллов» — это просто стандартизированная версия «баллов». Это случай идеальной мультиколлинеарности.
Если мы попытаемся подогнать модель множественной линейной регрессии в R, используя этот набор данных, мы не сможем произвести оценку коэффициента для предикторной переменной «масштабированные точки»:
#define data
df <- data.frame(rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))
df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)
#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)
#view summary of model
summary(model)
Call:
lm(formula = rating ~ pts + scaled_pts, data = df)
Residuals:
Min 1Q Median 3Q Max
-4.4932 -1.3941 -0.2935 1.3055 5.8412
Coefficients: (1 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 67.4218 3.5896 18.783 6.67e-08 \*\*\*
pts 0.8669 0.1527 5.678 0.000466 \*\*\*
scaled_pts NA NA NA NA
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663
3. Ловушка фиктивной переменной
Другой сценарий, в котором может иметь место идеальная мультиколлинеарность, известен как ловушка фиктивной переменной.Это когда мы хотим использовать категориальную переменную в регрессионной модели и преобразовать ее в «фиктивную переменную», которая принимает значения 0, 1, 2 и т. д.
Например, предположим, что мы хотели бы использовать предикторные переменные «возраст» и «семейное положение» для прогнозирования дохода:
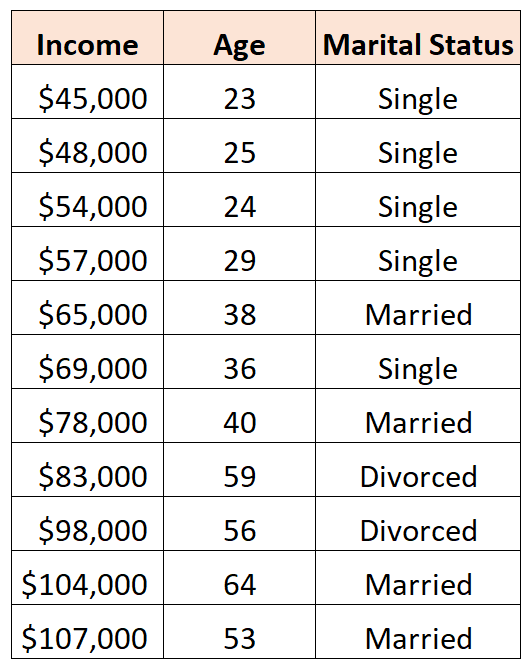
Чтобы использовать «семейное положение» в качестве переменной-предиктора, нам нужно сначала преобразовать его в фиктивную переменную.
Для этого мы можем позволить «Не замужем» быть нашим базовым значением, поскольку оно встречается чаще всего, и присвоить значения 0 или 1 «Женаты» и «Развод» следующим образом:
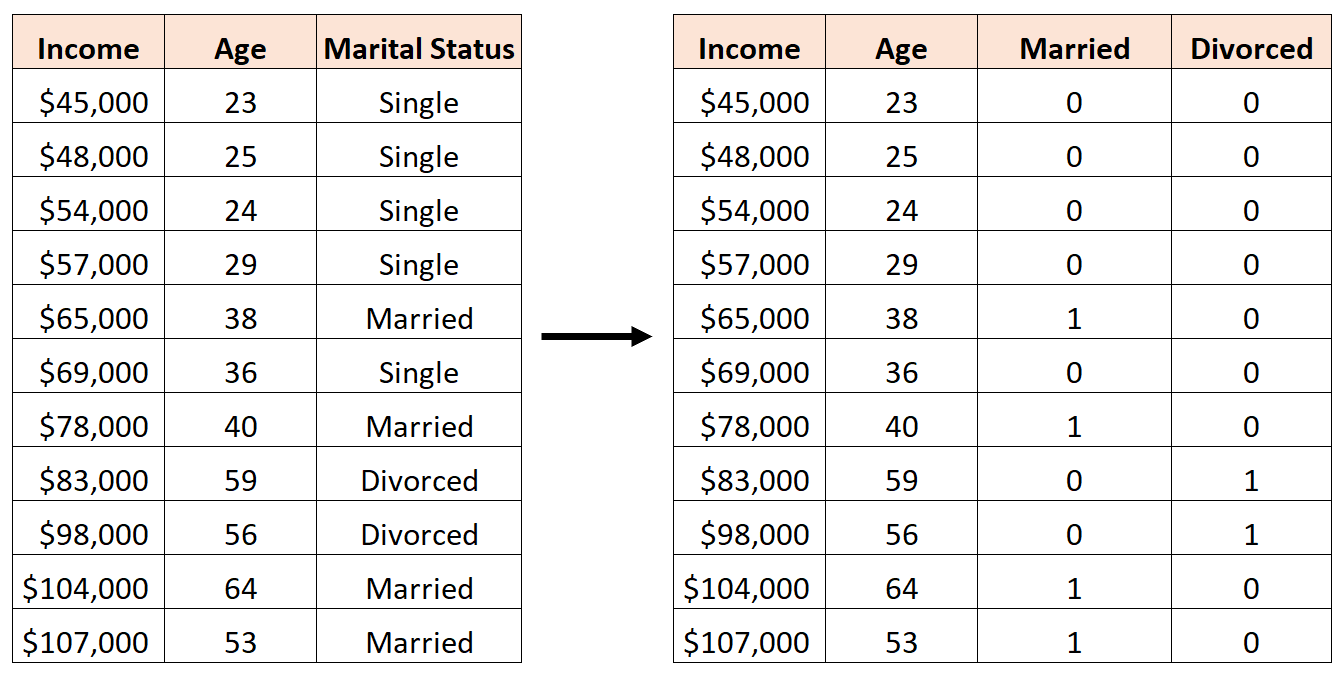
Ошибкой было бы создание трех новых фиктивных переменных следующим образом:
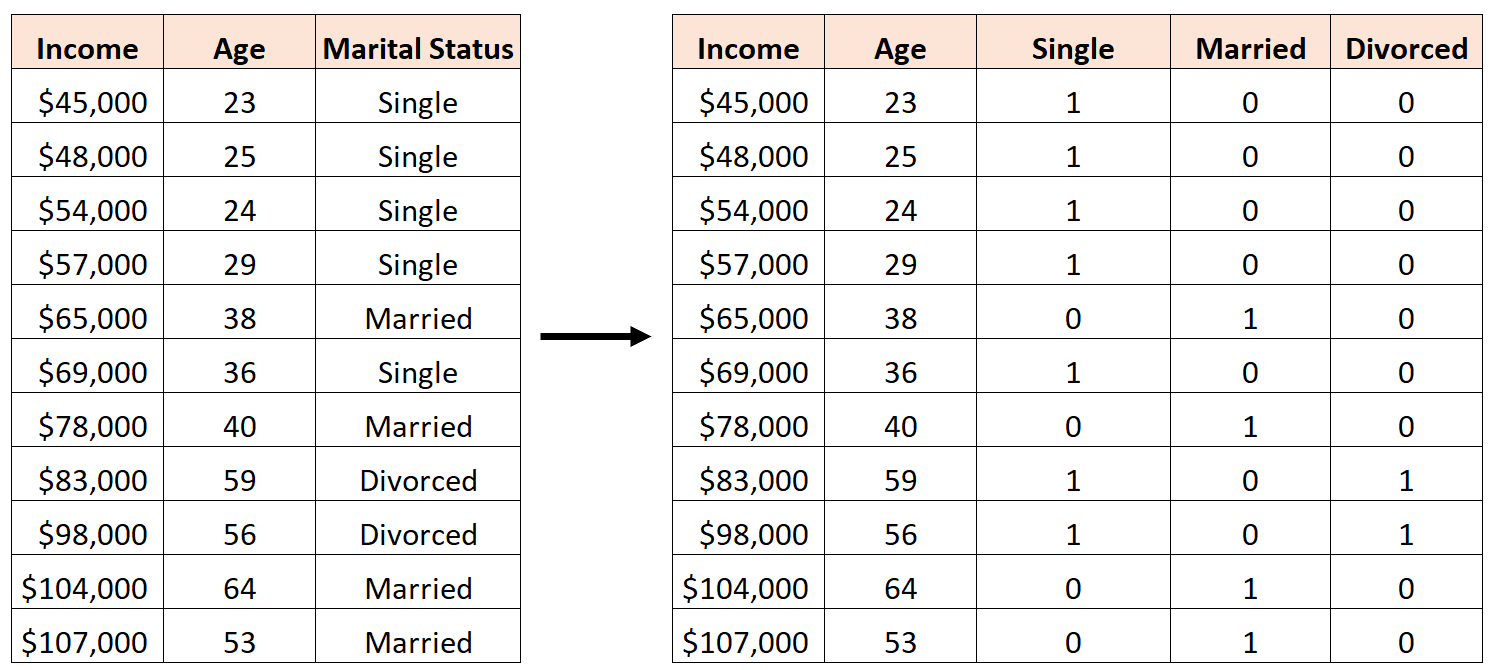
В этом случае переменная «Холост» является идеальной линейной комбинацией переменных «Женаты» и «Разведены». Это пример идеальной мультиколлинеарности.
Если мы попытаемся подогнать модель множественной линейной регрессии в R, используя этот набор данных, мы не сможем произвести оценку коэффициента для каждой переменной-предиктора:
#define data
df <- data.frame(income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))
#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)
#view summary of model
summary(model)
Call:
lm(formula = income ~ age + single + married + divorced, data = df)
Residuals:
Min 1Q Median 3Q Max
-9.7075 -5.0338 0.0453 3.3904 12.2454
Coefficients: (1 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.7559 17.7811 0.942 0.37739
age 1.4717 0.3544 4.152 0.00428 \*\*
single -2.4797 9.4313 -0.263 0.80018
married NA NA NA NA
divorced -8.3974 12.7714 -0.658 0.53187
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865
Дополнительные ресурсы
Руководство по мультиколлинеарности и VIF в регрессии
Как рассчитать VIF в R
Как рассчитать VIF в Python
Как рассчитать VIF в Excel