Линейная регрессия — это метод, который мы можем использовать для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной- откликом .
Обычно мы используем линейную регрессию с количественными переменными.Иногда называемые «числовыми» переменными, это переменные, которые представляют измеримую величину. Примеры включают:
- Количество квадратных метров в доме
- Численность населения города
- Возраст человека
Однако иногда мы хотим использовать категориальные переменные в качестве переменных-предикторов. Это переменные, которые принимают имена или метки и могут вписываться в категории. Примеры включают:
- Цвет глаз (например, «голубой», «зеленый», «карий»)
- Пол (например, «мужской», «женский»)
- Семейное положение (например, «замужем», «холост», «разведен»)
При использовании категориальных переменных не имеет смысла просто присваивать такие значения, как 1, 2, 3, таким значениям, как «синий», «зеленый» и «коричневый», потому что бессмысленно говорить, что зеленый дважды такой же красочный, как синий, или что коричневый в три раза красочнее синего.
Вместо этого решение состоит в использовании фиктивных переменных.Это переменные, которые мы создаем специально для регрессионного анализа и которые принимают одно из двух значений: ноль или единицу.
Количество фиктивных переменных, которые мы должны создать, равно k -1, где k — это количество различных значений, которые может принимать категориальная переменная.
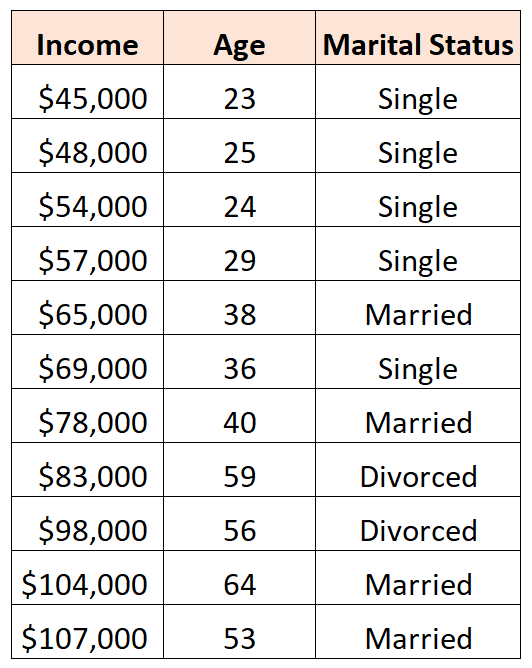
Например, предположим, что у нас есть следующий набор данных, и мы хотели бы использовать семейное положение и возраст для прогнозирования дохода :
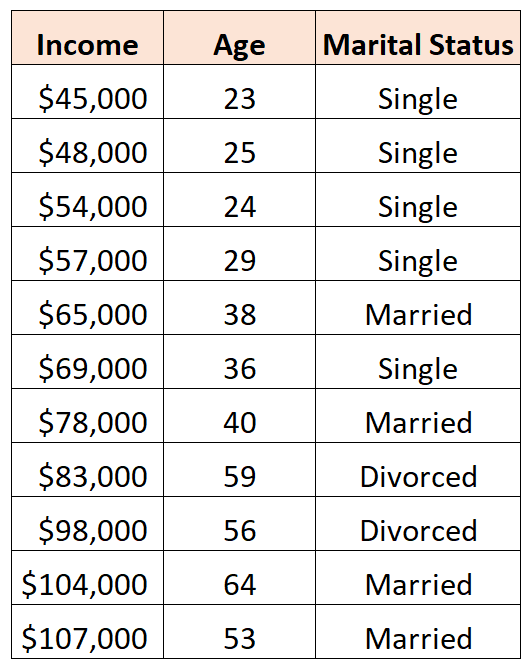
Чтобы использовать семейное положение в качестве предиктора в регрессионной модели, мы должны преобразовать его в фиктивную переменную.
Поскольку в настоящее время это категориальная переменная, которая может принимать три разных значения («Холост», «Женат» или «Разведен»), нам нужно создать k -1 = 3-1 = 2 фиктивных переменных.
Чтобы создать эту фиктивную переменную, мы можем позволить «Single» быть нашим базовым значением, поскольку оно встречается чаще всего. Таким образом, вот как мы можем преобразовать семейное положение в фиктивные переменные:
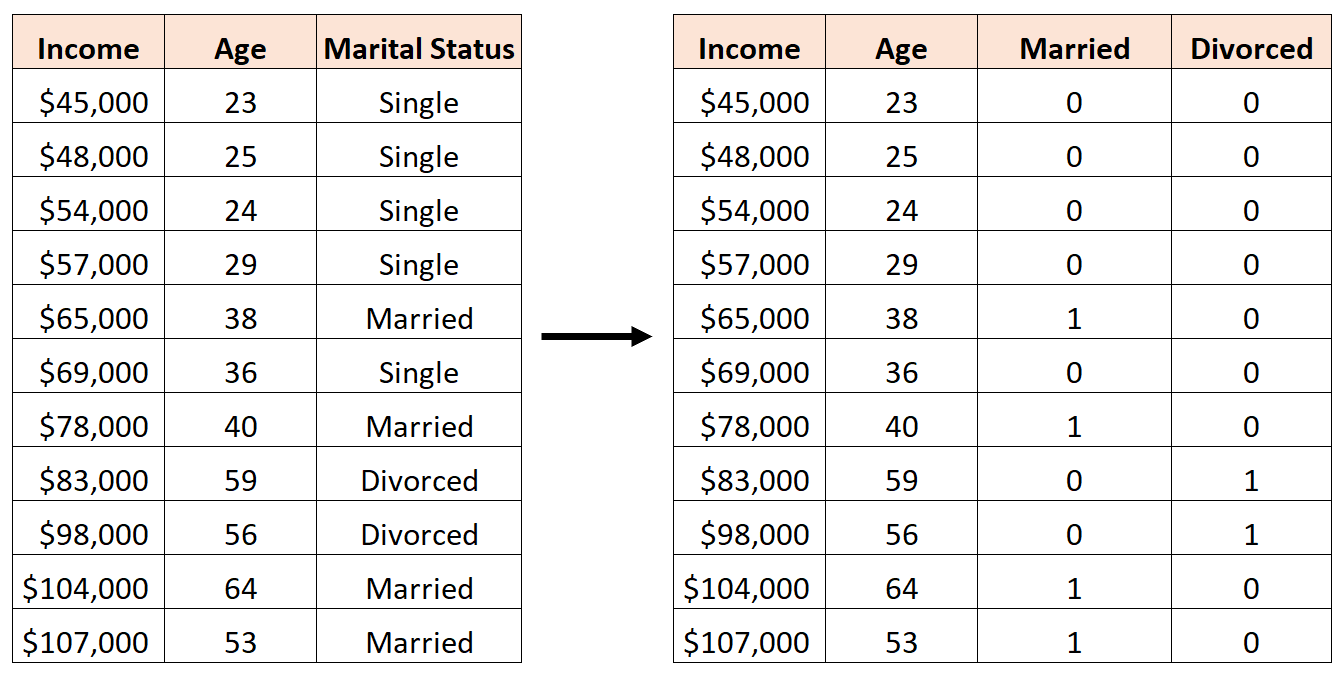
Затем мы могли бы использовать Age , Married и Divorced в качестве переменных-предикторов в регрессионной модели.
При создании фиктивных переменных может возникнуть проблема, известная как ловушка фиктивных переменных.Это происходит, когда мы создаем k фиктивных переменных вместо k -1 фиктивных переменных.
Когда это произойдет, по крайней мере две фиктивные переменные будут страдать от идеальной мультиколлинеарности.То есть они будут идеально коррелированы. Это приводит к неверным расчетам коэффициентов регрессии и соответствующих им p-значений.
Ловушка фиктивных переменных: когда количество созданных фиктивных переменных равно количеству значений, которые может принимать категориальное значение. Это приводит к мультиколлинеарности, что приводит к неправильным расчетам коэффициентов регрессии и p-значений.
Например, предположим, что мы преобразовали семейное положение в следующие фиктивные переменные:
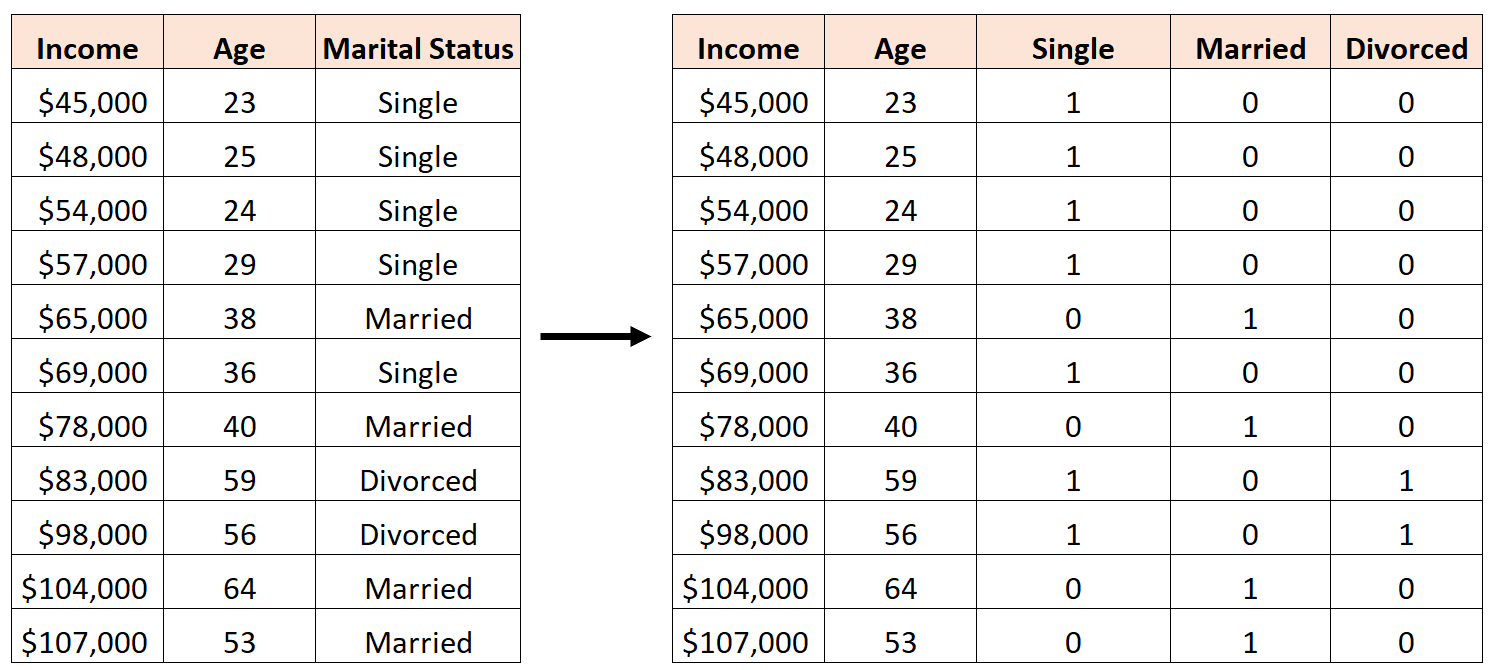
В этом случае Холостые и Женатые прекрасно коррелируют и имеют коэффициент корреляции -1.
Таким образом, когда мы перейдем к выполнению множественной линейной регрессии, расчеты коэффициентов регрессии будут неверными.
Как избежать ловушки фиктивных переменных
Вам нужно запомнить только одно правило, чтобы избежать ловушки фиктивной переменной:
Если категориальная переменная может принимать k различных значений, вам следует создать только k-1 фиктивных переменных для использования в регрессионной модели.
Например, предположим, что вы хотите преобразовать категориальную переменную «учебный год» в фиктивные переменные. Предположим, что эта переменная принимает следующие значения:
- Первокурсник
- второкурсник
- Джуниор
- Старший
Поскольку эта переменная может принимать 4 разных значения, мы создадим только 3 фиктивные переменные. Например, наши фиктивные переменные могут быть:
- Х 1 = 1, если второкурсник; 0 иначе
- Х 2 = 1, если Младший; 0 иначе
- Х 3 = 1, если старший; 0 иначе
Поскольку количество фиктивных переменных на единицу меньше, чем количество значений, которые может принимать «учебный год», мы можем избежать ловушки фиктивных переменных и проблемы мультиколлинеарности.
Дополнительные ресурсы
Как использовать фиктивные переменные в регрессионном анализе
Введение в множественную линейную регрессию
Руководство по мультиколлинеарности в регрессии