Полиномиальная регрессия — это метод, который мы можем использовать, когда связь между переменной-предиктором и переменной- ответом нелинейна.
Этот тип регрессии принимает форму:
Y = β 0 + β 1 X + β 2 X 2 + … + β h X h + ε
где h — «степень» многочлена.
В этом руководстве представлен пошаговый пример выполнения полиномиальной регрессии в R.
Шаг 1: Создайте данные
В этом примере мы создадим набор данных, который содержит количество часов обучения и итоговый балл за экзамен для класса из 50 студентов:
#make this example reproducible
set.seed(1)
#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours\* runif (50, 1, 2)
#view first six rows of data
head(data)
hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510
Шаг 2: Визуализируйте данные
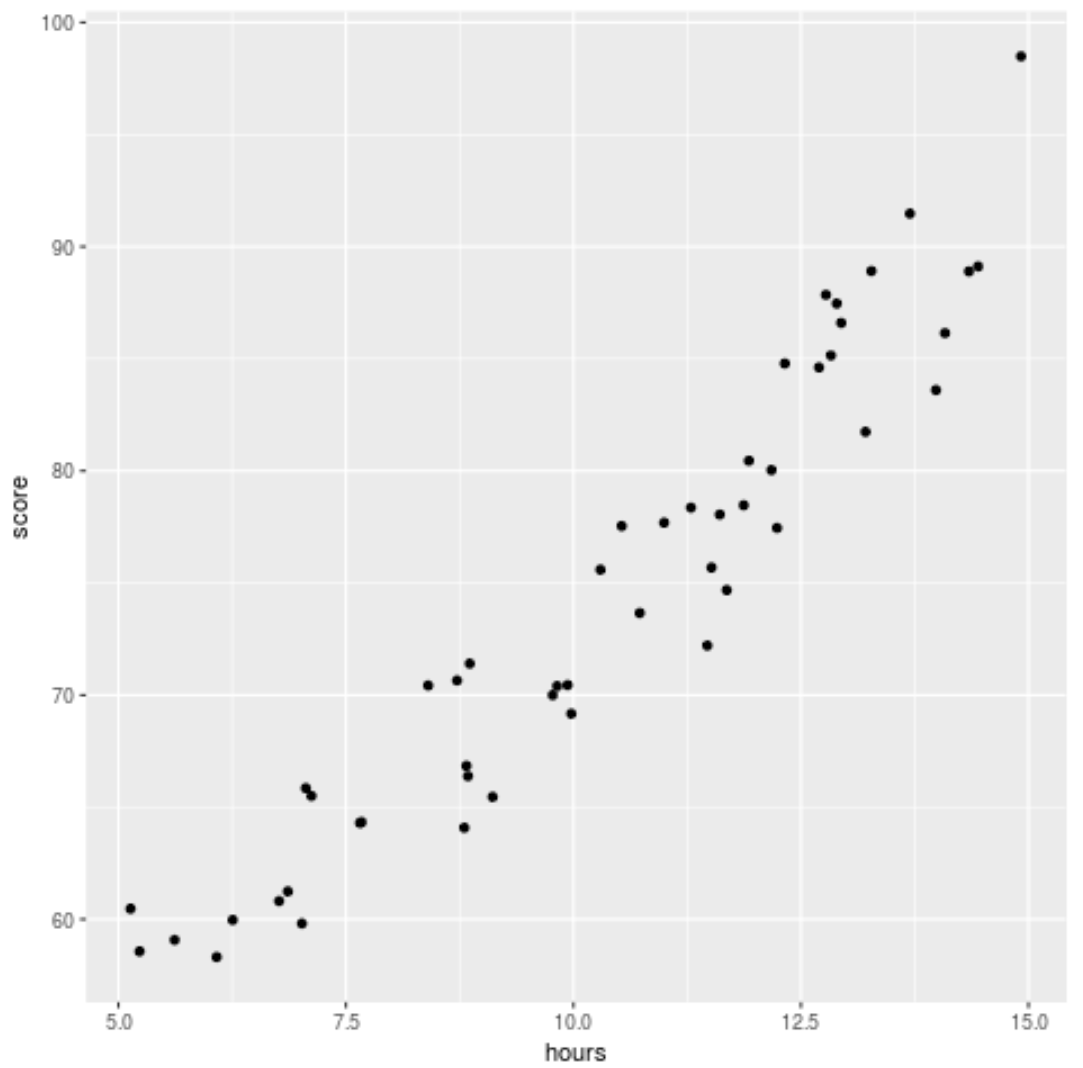
Прежде чем мы подгоним модель регрессии к данным, давайте сначала создадим диаграмму рассеяния, чтобы визуализировать взаимосвязь между отработанными часами и экзаменационным баллом:
library (ggplot2)
ggplot(df, aes (x=hours, y=score)) +
geom_point()
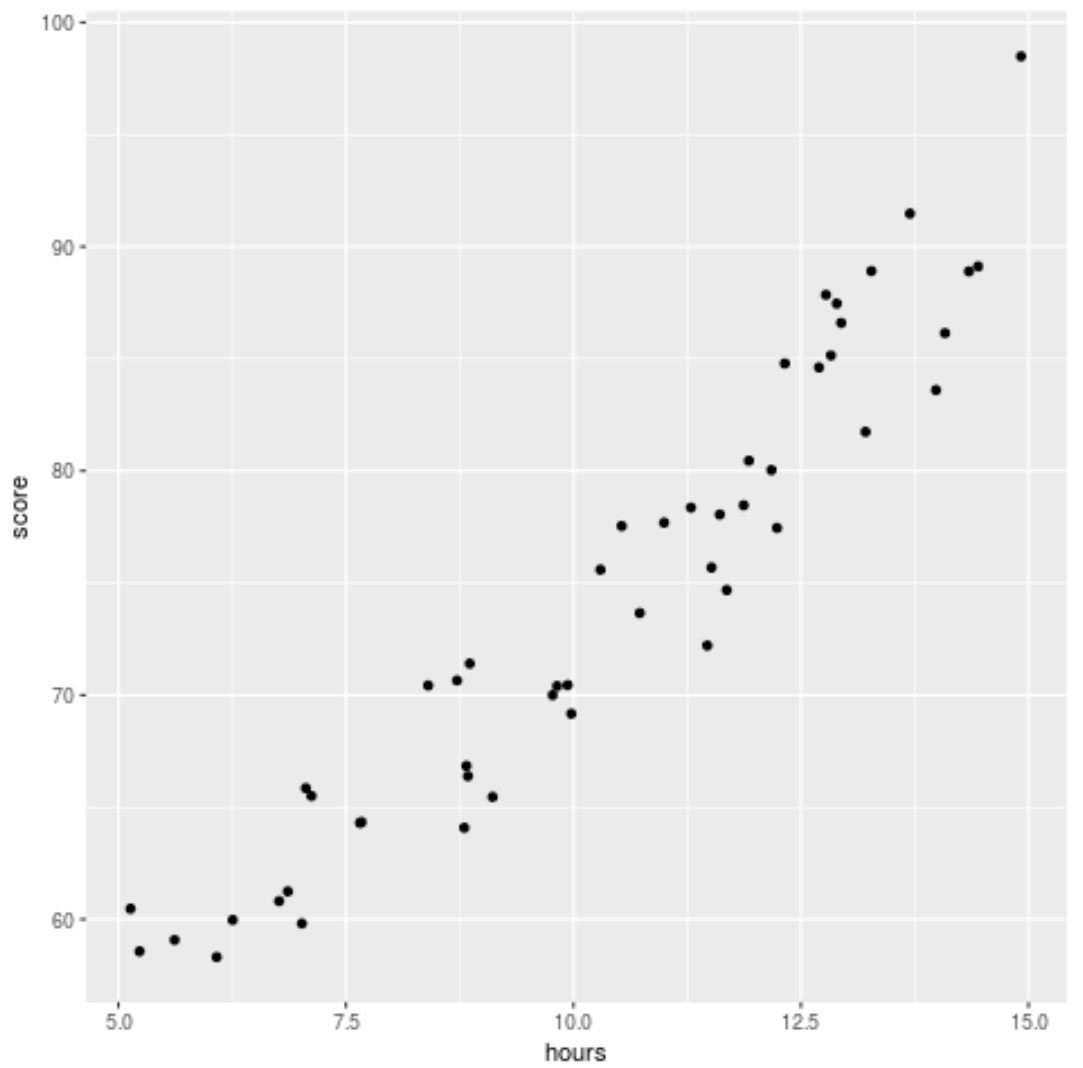
Мы видим, что данные демонстрируют некоторую квадратичную зависимость, что указывает на то, что полиномиальная регрессия может соответствовать данным лучше, чем простая линейная регрессия.
Шаг 3: Подберите модели полиномиальной регрессии
Затем мы подберем пять различных моделей полиномиальной регрессии со степенями h = 1…5 и используем перекрестную проверку k-кратного порядка с k = 10-кратным, чтобы вычислить тестовую MSE для каждой модели:
#randomly shuffle data
df.shuffled <- df[ sample ( nrow(df)),]
#define number of folds to use for k-fold cross-validation
K <- 10
#define degree of polynomials to fit
degree <- 5
#create k equal-sized folds
folds <- cut( seq (1, nrow(df.shuffled)),breaks=K,labels= FALSE )
#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)
#Perform K-fold cross validation
for (i in 1:K){
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
testData <- df.shuffled[testIndexes, ]
trainData <- df.shuffled[-testIndexes, ]
#use k-fold cv to evaluate models
for (j in 1:degree){
fit.train = lm (score ~ poly (hours,j), data=trainData)
fit.test = predict (fit.train, newdata=testData)
mse[i,j] = mean ((fit.test-testData$score)^2)
}
}
#find MSE for each degree
colMeans(mse)
[1] 9.802397 8.748666 9.601865 10.592569 13.545547
Из вывода мы можем увидеть тест MSE для каждой модели:
- СКО теста со степенью h = 1: 9,80
- СКО теста со степенью h = 2: 8,75
- СКО теста со степенью h = 3: 9,60
- СКО теста со степенью h = 4: 10,59
- СКО теста со степенью h = 5: 13,55
Модель с наименьшей тестовой MSE оказалась моделью полиномиальной регрессии со степенью h =2.
Это соответствует нашей интуиции из исходной диаграммы рассеяния: модель квадратичной регрессии лучше всего соответствует данным.
Шаг 4: Анализ окончательной модели
Наконец, мы можем получить коэффициенты наиболее эффективной модели:
#fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)
#view summary of best model
summary(best)
Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)
Residuals:
Min 1Q Median 3Q Max
-5.6589 -2.0770 -0.4599 2.5923 4.5122
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 54.00526 5.52855 9.768 6.78e-13 \*\*\*
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 \*\*
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Из вывода мы видим, что окончательная подогнанная модель:
Оценка = 54,00526 – 0,07904*(часы) + 0,18596*(часы) 2
Мы можем использовать это уравнение для оценки балла, который получит учащийся в зависимости от количества часов, которые он проучился.
Например, ожидается, что студент, который занимается 10 часов, получит 71,81 балла:
Оценка = 54,00526 – 0,07904*(10) + 0,18596*(10) 2 = 71,81
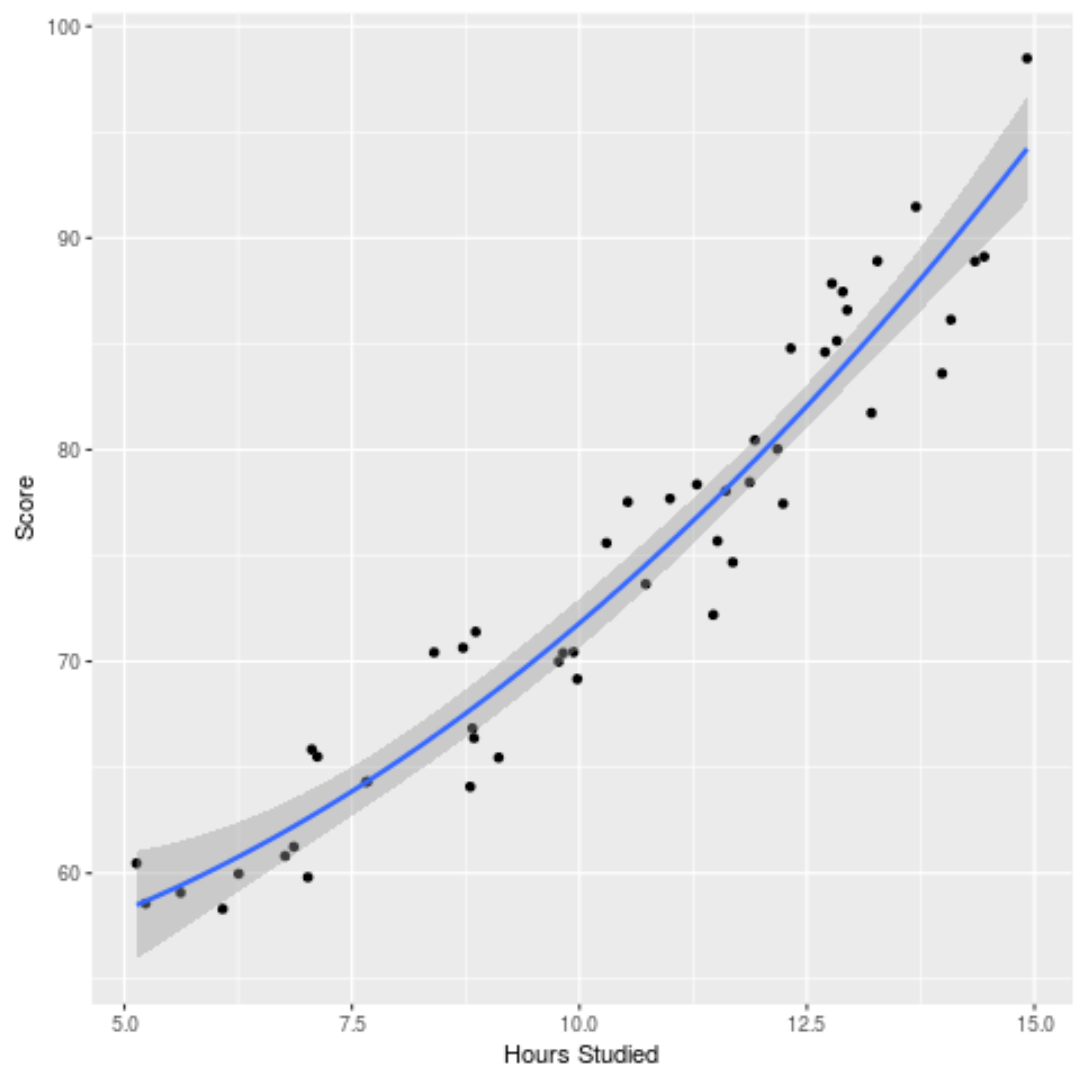
Мы также можем построить построенную модель, чтобы увидеть, насколько хорошо она соответствует необработанным данным:
ggplot(df, aes (x=hours, y=score)) +
geom_point() +
stat_smooth(method='lm', formula = y ~ poly (x,2), size = 1) +
xlab('Hours Studied') +
ylab('Score')
Полный код R, использованный в этом примере, вы можете найти здесь .