Степенная регрессия — это тип нелинейной регрессии, который принимает следующую форму:
у = топор б
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
Этот тип регрессии используется для моделирования ситуаций, когда переменная ответа равна переменной предиктора, возведенной в степень.
В следующем пошаговом примере показано, как выполнить регрессию мощности для заданного набора данных в R.
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельные данные для двух переменных: x и y.
#create data
x=1:20
y=c(1, 8, 5, 7, 6, 20, 15, 19, 23, 37, 33, 38, 49, 50, 56, 52, 70, 89, 97, 115)
Шаг 2: Визуализируйте данные
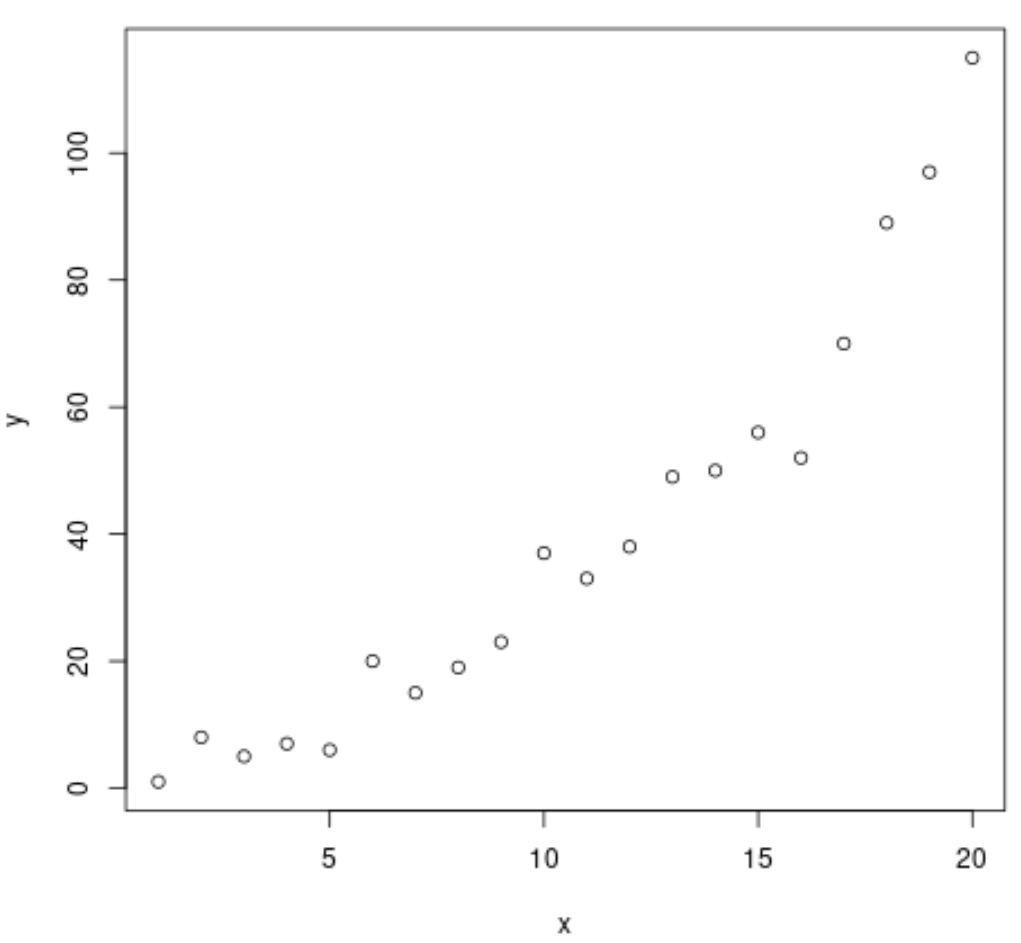
Затем создадим диаграмму рассеяния, чтобы визуализировать взаимосвязь между x и y:
#create scatterplot
plot(x, y)

Из графика видно, что между двумя переменными существует четкая степенная зависимость. Таким образом, представляется хорошей идеей использовать уравнение степенной регрессии для данных вместо модели линейной регрессии.
Шаг 3: Подберите модель регрессии мощности
Далее мы воспользуемся функцией lm() , чтобы подобрать модель регрессии к данным, указав, что R должен использовать журнал переменной ответа и журнал переменной-предиктора при подборе модели:
#fit the model
model <- lm(log(y)~ log(x))
#view the output of the model
summary(model)
Call:
lm(formula = log(y) ~ log(x))
Residuals:
Min 1Q Median 3Q Max
-0.67014 -0.17190 -0.05341 0.16343 0.93186
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.15333 0.20332 0.754 0.461
log(x) 1.43439 0.08996 15.945 4.62e-12 \*\*\*
---
Signif. codes: 0 ‘\*\*\*’ 0.001 ‘\*\*’ 0.01 ‘\*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3187 on 18 degrees of freedom
Multiple R-squared: 0.9339, Adjusted R-squared: 0.9302
F-statistic: 254.2 on 1 and 18 DF, p-value: 4.619e-12
Общее значение F модели составляет 252,1, а соответствующее значение p чрезвычайно мало (4,619e-12), что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что соответствующее уравнение регрессии мощности выглядит следующим образом:
ln(y) = 0,15333 + 1,43439ln(x)
Применив e к обеим частям, мы можем переписать уравнение как:
- у = е 0,15333 + 1,43439ln(х)
- у = 1,1657 х 1,43439
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x .
Например, если x = 12, то мы можем предсказать, что y будет равно 41,167 :
у = 1,1657(12) 1,43439 = 41,167
Бонус: не стесняйтесь использовать этот онлайн- калькулятор регрессии мощности для автоматического вычисления уравнения регрессии мощности для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить множественную линейную регрессию в R
Как выполнить экспоненциальную регрессию в R
Как выполнить логарифмическую регрессию в R