Экспоненциальная регрессия — это тип регрессии, который можно использовать для моделирования следующих ситуаций:
1. Экспоненциальный рост: рост начинается медленно, а затем стремительно ускоряется без ограничений.
2. Экспоненциальное затухание: затухание начинается быстро, а затем замедляется, приближаясь к нулю.

Уравнение модели экспоненциальной регрессии принимает следующий вид:
у = аб х
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить экспоненциальную регрессию в R.
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельные данные для двух переменных: x и y :
x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)
Шаг 2: Визуализируйте данные
Затем давайте создадим быструю диаграмму рассеяния, чтобы визуализировать взаимосвязь между x и y :
plot(x, y)
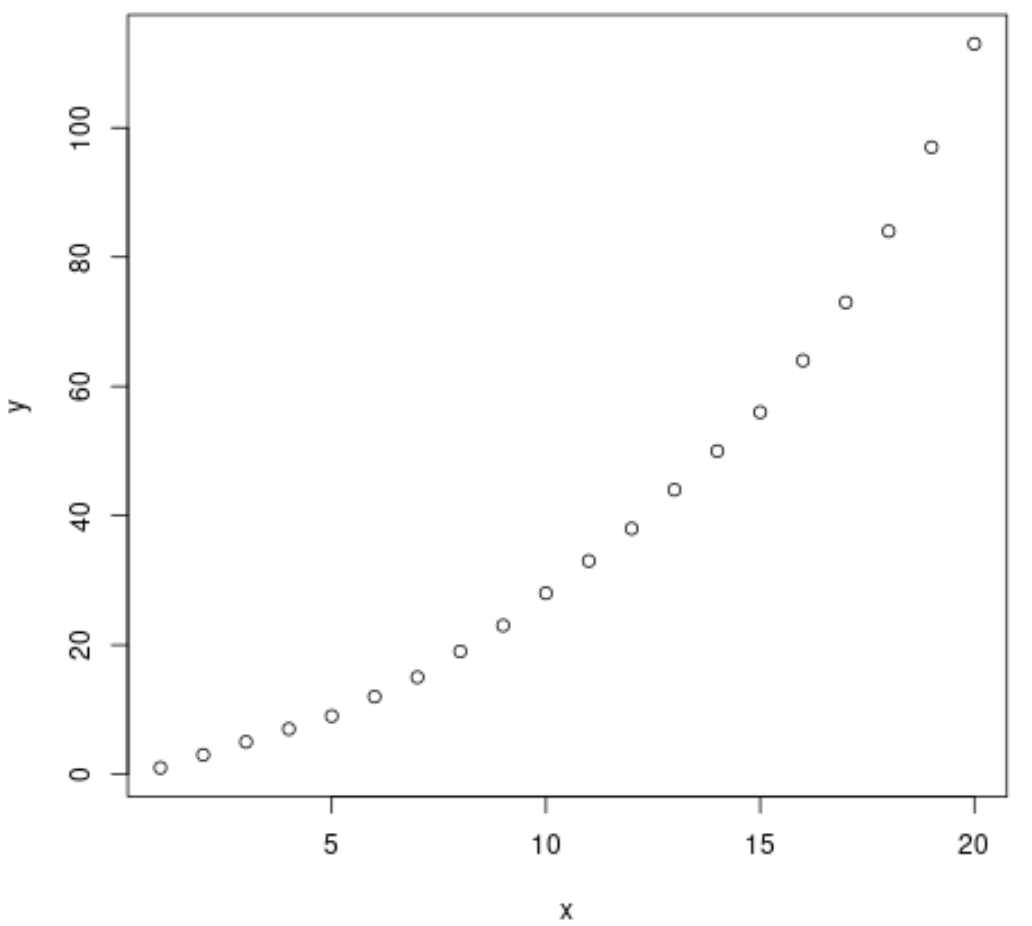
Из графика видно, что существует четкая экспоненциальная модель роста между двумя переменными.
Таким образом, кажется хорошей идеей подобрать уравнение экспоненциальной регрессии для описания взаимосвязи между переменными.
Шаг 3: Подберите модель экспоненциальной регрессии
Далее мы воспользуемся функцией lm() , чтобы подобрать модель экспоненциальной регрессии, используя натуральный логарифм y в качестве переменной ответа и x в качестве переменной-предиктора:
#fit the model
model <- lm( log (y)~ x)
#view the output of the model
summary(model)
Call:
lm(formula = log(y) ~ x)
Residuals:
Min 1Q Median 3Q Max
-1.1858 -0.1768 0.1104 0.2720 0.3300
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.98166 0.17118 5.735 1.95e-05 \*\*\*
x 0.20410 0.01429 14.283 2.92e-11 \*\*\*
---
Signif. codes: 0 ‘\*\*\*’ 0.001 ‘\*\*’ 0.01 ‘\*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11
Общее F-значение модели равно 204, а соответствующее p-значение чрезвычайно мало (2,917e-11), что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение экспоненциальной регрессии:
ln(у) = 0,9817 + 0,2041(х)
Применив e к обеим частям, мы можем переписать уравнение как:
у = 2,6689 * 1,2264 х
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 12, то мы можем предсказать, что y будет равно 30,897 :
у = 2,6689 * 1,2264 12 = 30,897
Бонус: не стесняйтесь использовать этот онлайн- калькулятор экспоненциальной регрессии для автоматического вычисления уравнения экспоненциальной регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить квадратичную регрессию в R
Как выполнить полиномиальную регрессию в R