Выборочная дисперсия говорит нам, насколько разбросаны значения в данной выборке .
Обычно обозначаемый как s 2 , он рассчитывается как:
s 2 = Σ (x i – x ) 2 / (n-1)
куда:
- x : выборочное среднее
- x i : i -е значение в выборке
- n : размер выборки
В следующем пошаговом примере показано, как рассчитать выборочную дисперсию для следующей выборки:
Пример: 2, 4, 4, 7, 8, 12, 14, 15, 19, 22
Шаг 1: введите данные
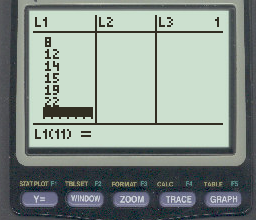
Сначала мы введем значения данных.
Нажмите Stat , затем нажмите EDIT.Затем введите значения выборки в столбец L1:
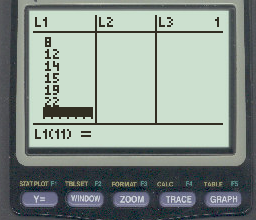
Шаг 2: Найдите выборочную дисперсию
Затем нажмите Stat , а затем прокрутите вправо и нажмите CALC .
Затем нажмите 1-Var Stats .
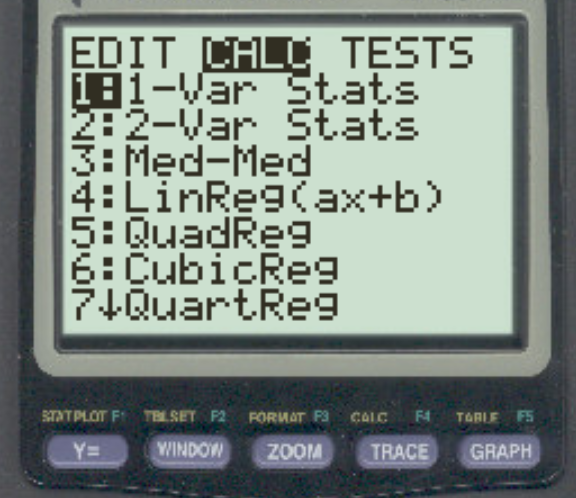
В появившемся новом экране нажмите Enter .

Как только вы нажмете Enter , появится список сводной статистики.
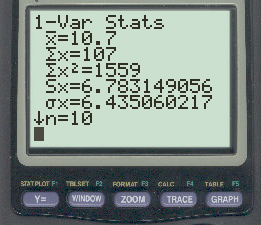
Стандартное отклонение выборки равно Sx = 6,783149056 .
Чтобы найти выборочную дисперсию, нам нужно возвести это значение в квадрат. Для этого нажмите VARS , а затем нажмите 5:
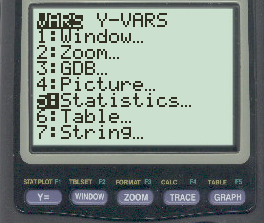
В появившемся новом окне нажмите 3, чтобы выбрать стандартное отклонение выборки:
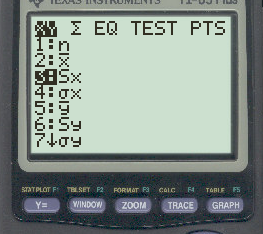
Наконец, нажмите кнопку x 2 , чтобы возвести стандартное отклонение выборки в квадрат:
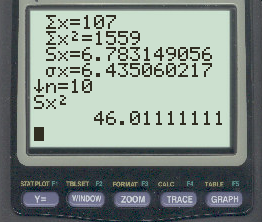
Выборочная дисперсия оказывается равной 46,0111 .
Дополнительные ресурсы
Как найти сводку из пяти чисел на калькуляторе TI-84
Как найти межквартильный диапазон на калькуляторе TI-84
Как найти коэффициент вариации на калькуляторе TI-84