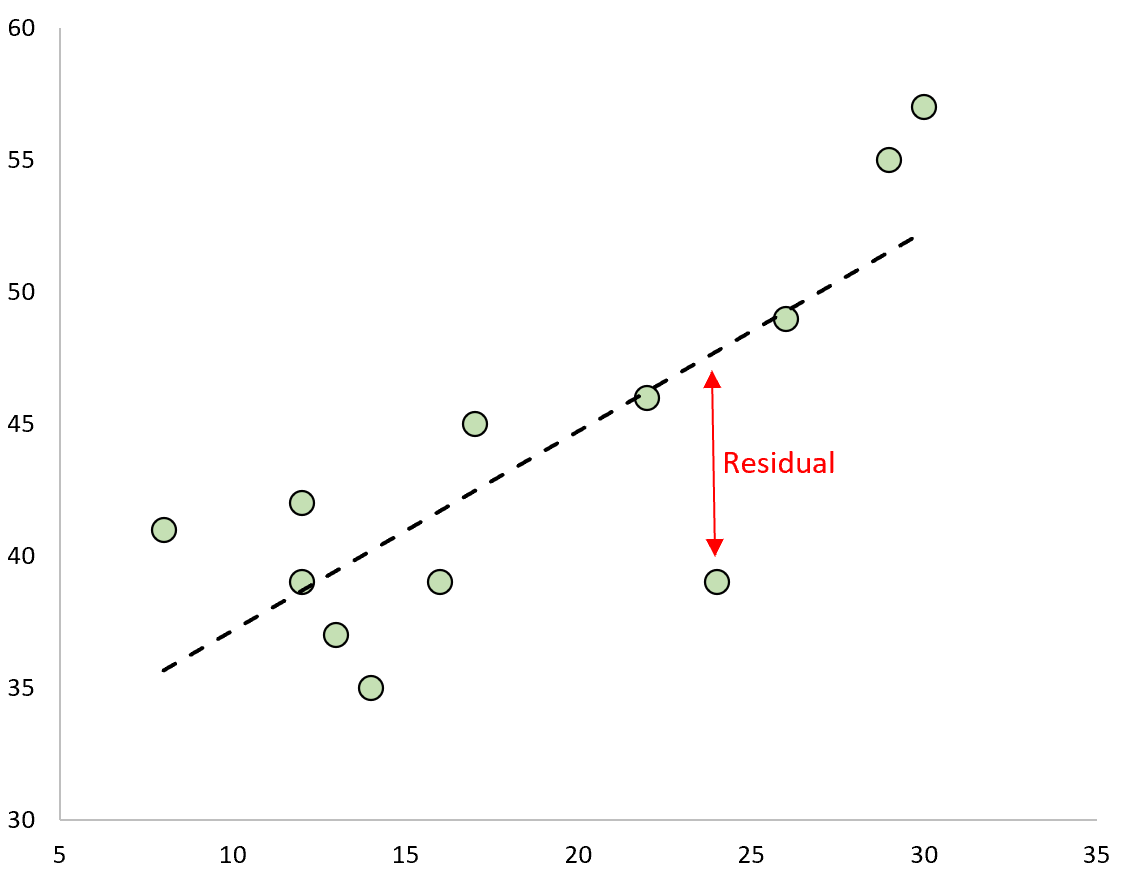
Остаток — это разница между наблюдаемым значением и прогнозируемым значением в регрессионной модели .
Он рассчитывается как:
Остаток = наблюдаемое значение – прогнозируемое значение
Если мы нанесем наблюдаемые значения и наложим подобранную линию регрессии, остатки для каждого наблюдения будут вертикальным расстоянием между наблюдением и линией регрессии:
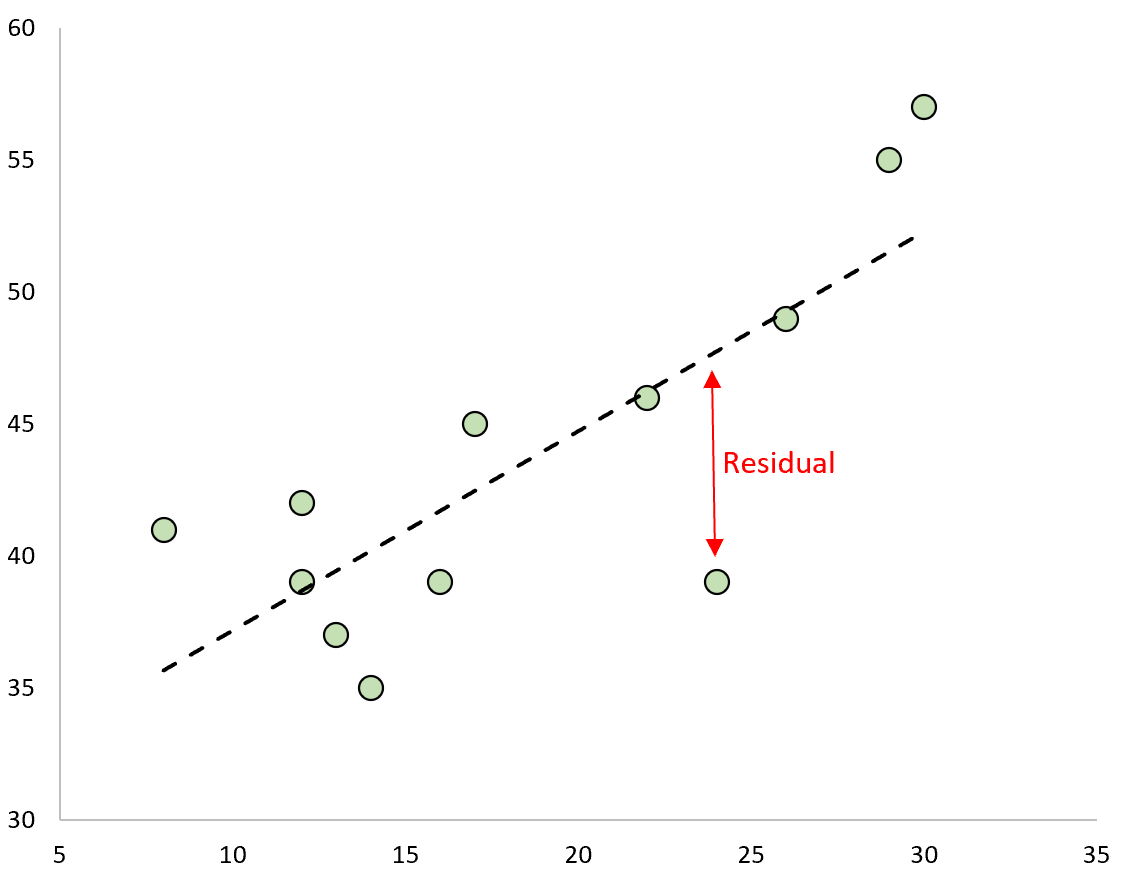
Один тип остатка, который мы часто используем для выявления выбросов в регрессионной модели, известен как стандартизированный остаток .
Он рассчитывается как:
r i = e i / s(e i ) = e i / RSE√ 1-h ii
куда:
- e i : i -й остаток
- RSE: остаточная стандартная ошибка модели.
- h ii : рычаг i -го наблюдения
На практике мы часто считаем выбросом любой стандартизованный остаток с абсолютным значением больше 3.
В этом руководстве представлен пошаговый пример расчета стандартизованных остатков в Excel.
Шаг 1: введите данные
Сначала мы введем значения для небольшого набора данных в Excel:
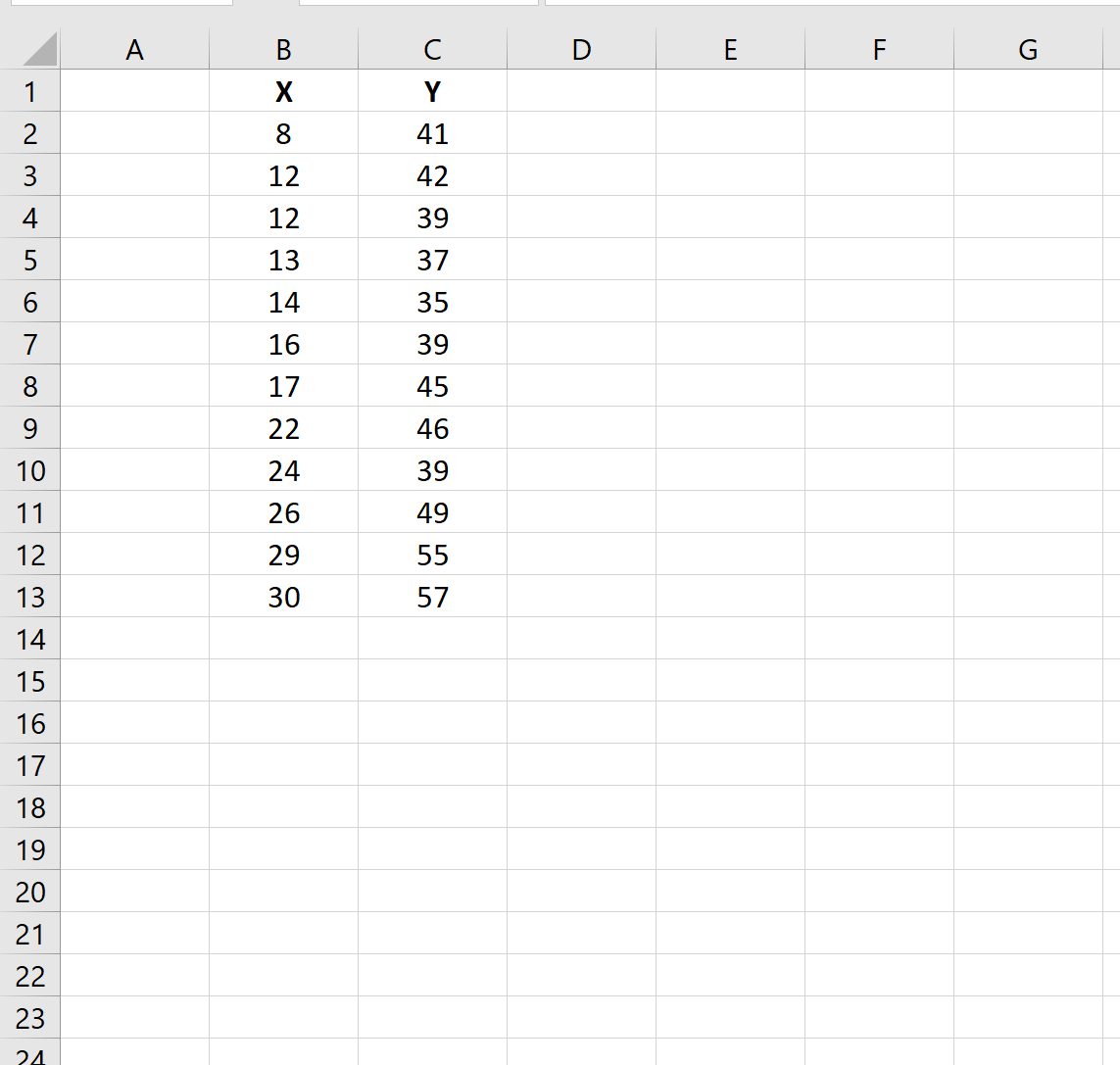
Шаг 2: Рассчитайте остатки
Затем мы перейдем на вкладку « Данные » на верхней ленте и нажмем « Анализ данных» в группе « Анализ »:

Если вы еще не установили эту надстройку, ознакомьтесь с этим руководством , чтобы узнать, как это сделать. Его легко установить и совершенно бесплатно.
После того, как вы нажали «Анализ данных», выберите параметр « Регрессия » и нажмите « ОК ». В появившемся новом окне заполните следующую информацию и нажмите OK :
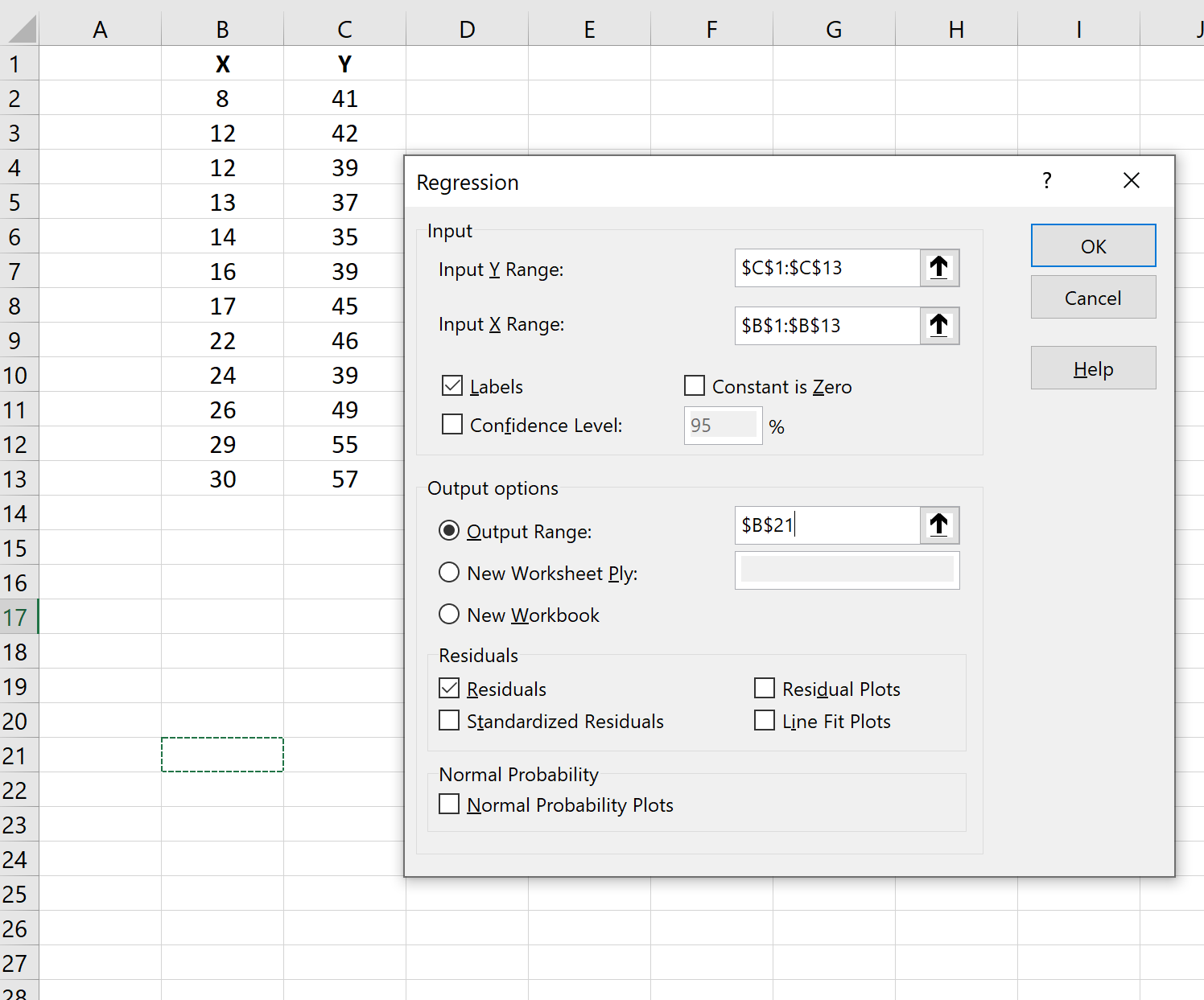
Остаток для каждого наблюдения появится в выводе:
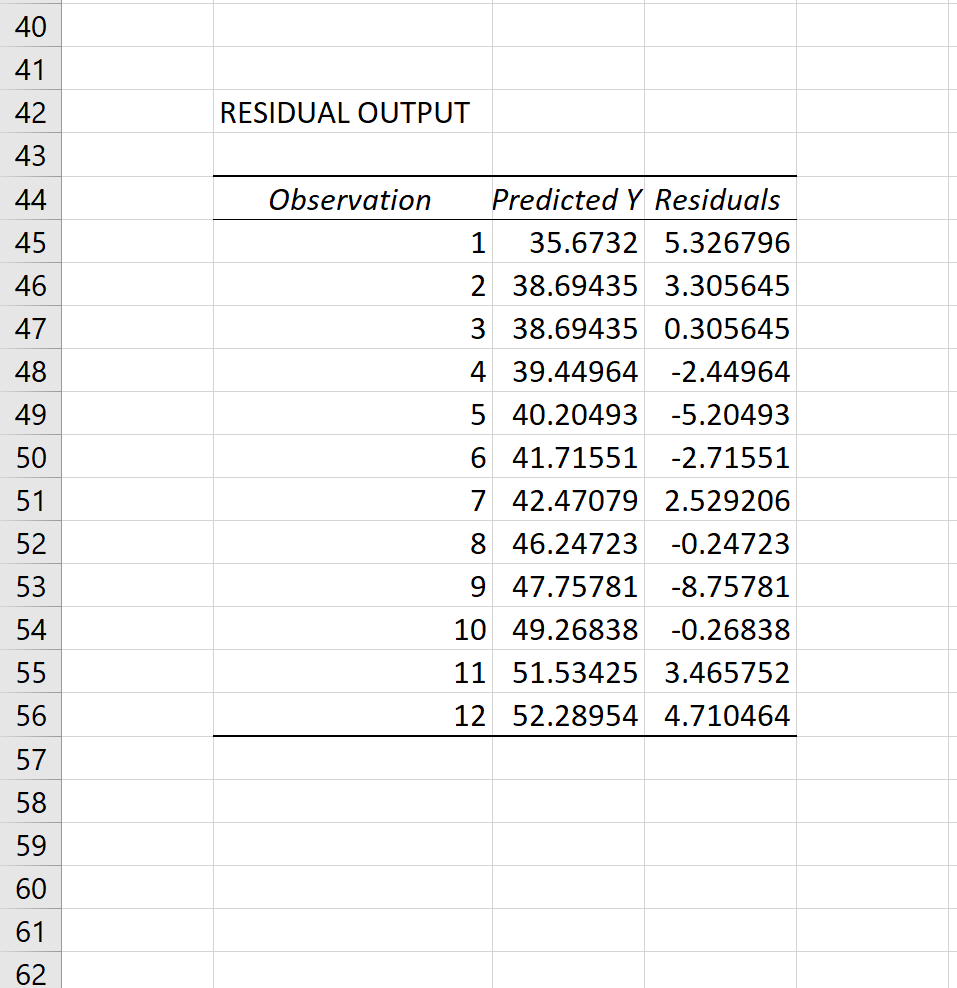
Скопируйте и вставьте эти остатки в новый столбец рядом с исходными данными:
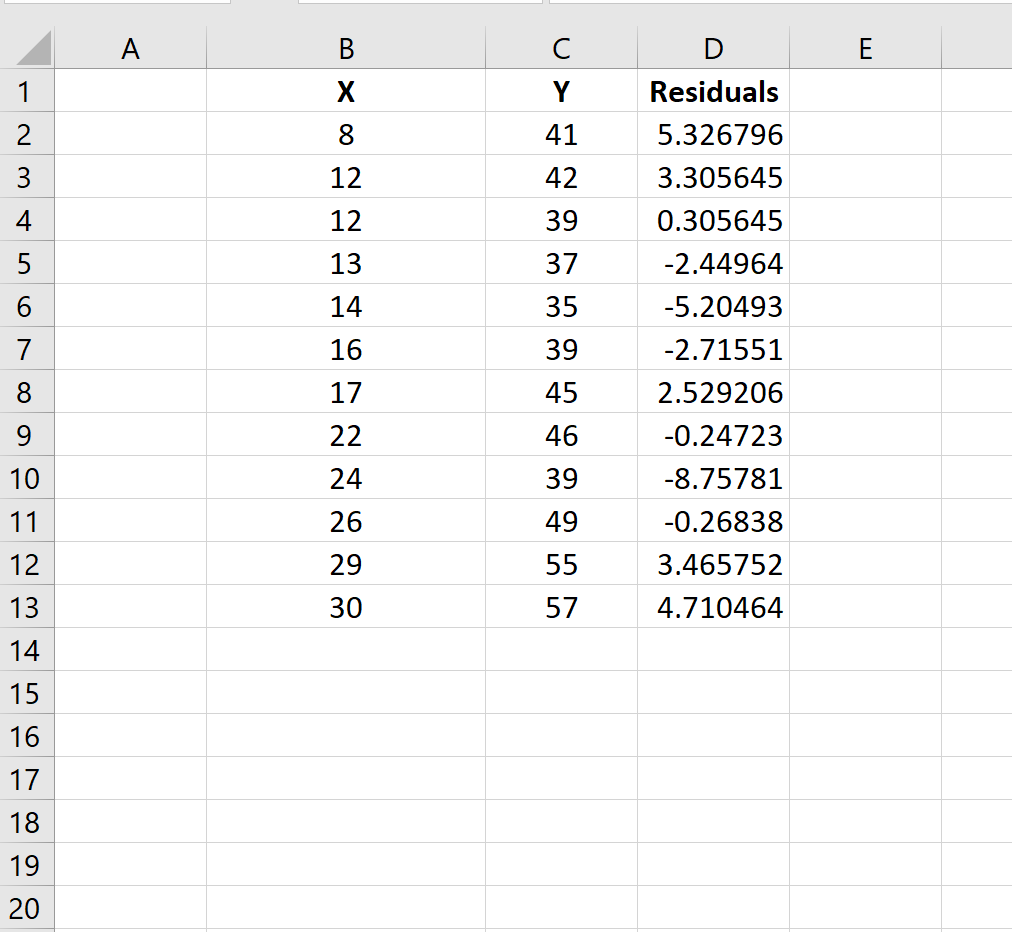
Шаг 3: Рассчитайте кредитное плечо
Далее нам нужно рассчитать кредитное плечо каждого наблюдения.
На следующем изображении показано, как это сделать:
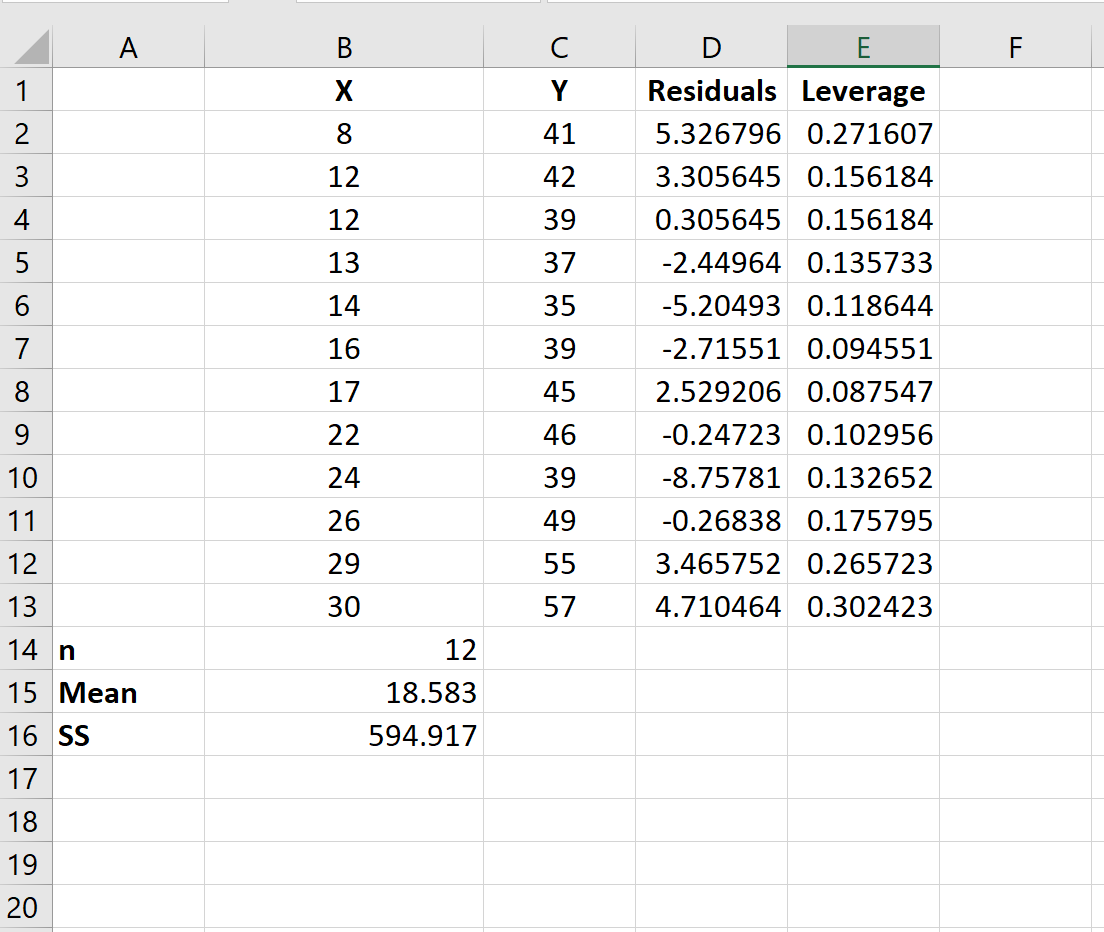
Вот формулы, используемые в различных ячейках:
- B14: =СЧЁТ(B2:B13)
- B15: =СРЕДНЕЕ(B2:B13)
- B16: =DEVSQ(B2:B13)
- E2: =1/$B$14+(B2-$B$15)^2/$B$16
Шаг 4: Рассчитайте стандартизированные остатки
Наконец, мы можем рассчитать стандартизованные остатки по формуле:
r i = e i / RSE √ 1-h ii
RSE для модели можно найти в выходных данных модели ранее. Получается 4,44 :
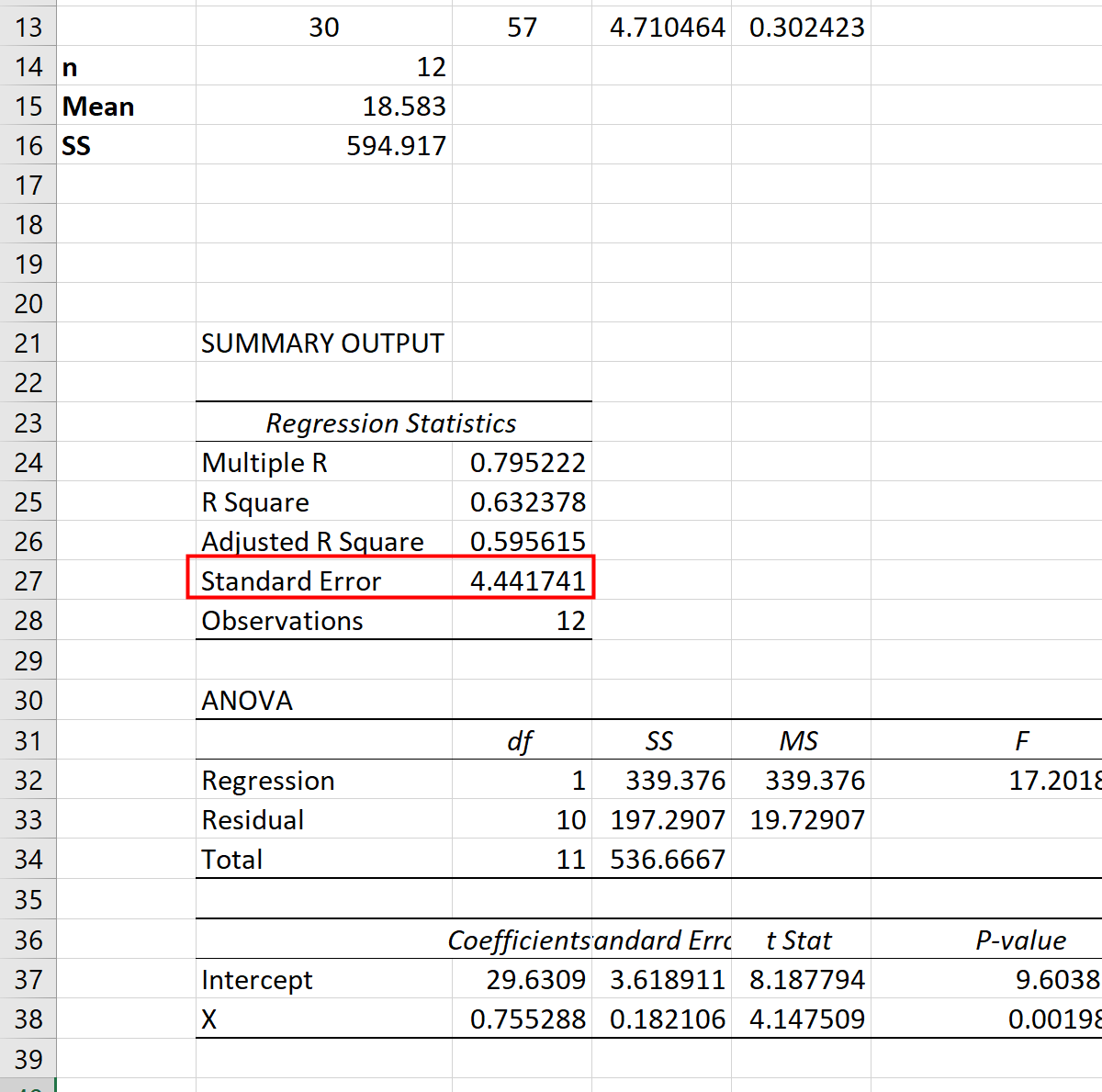
Таким образом, мы можем использовать следующую формулу для расчета стандартизованного остатка для каждого наблюдения:
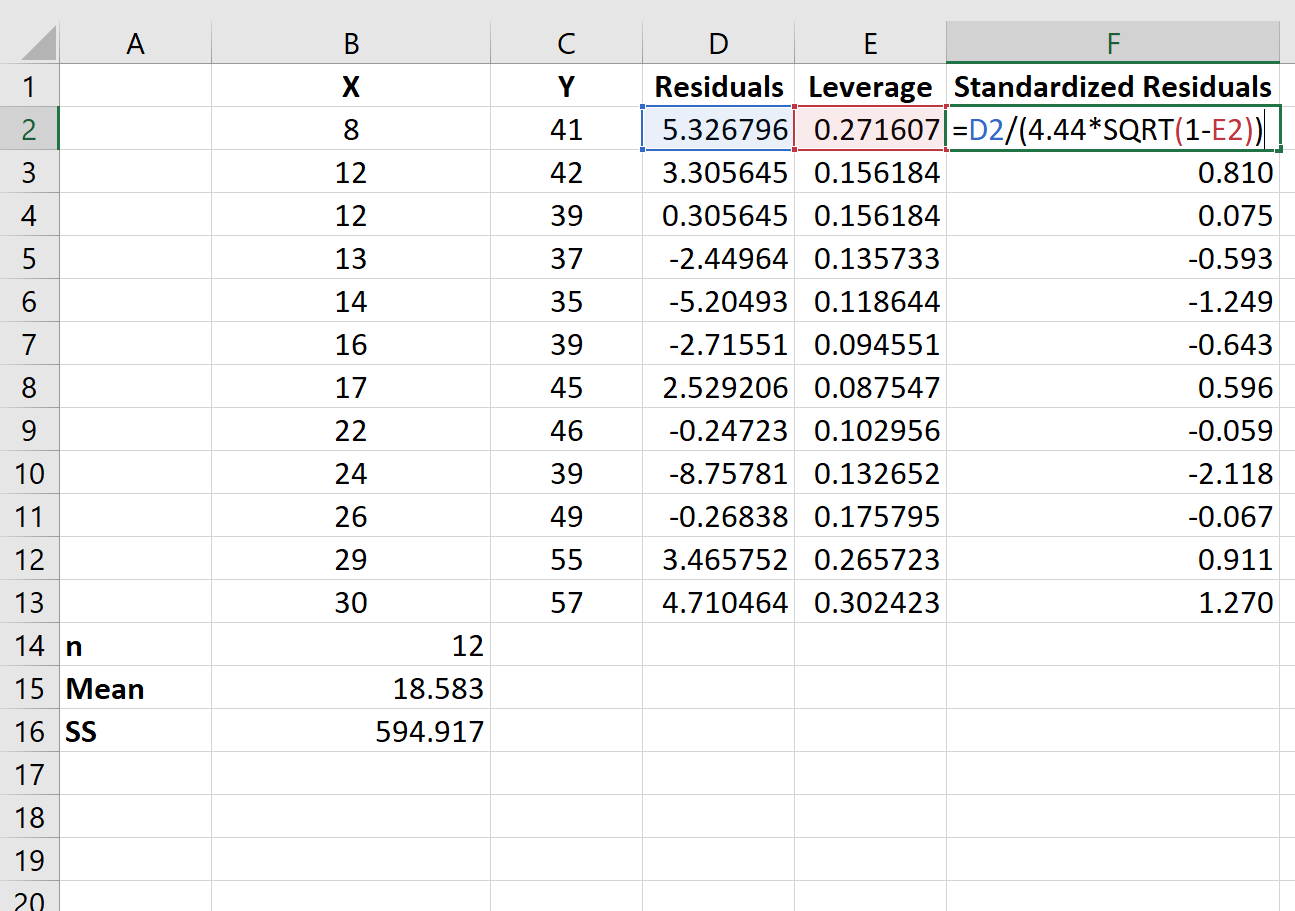
Из результатов видно, что ни один из стандартизированных остатков не превышает абсолютного значения 3. Таким образом, ни одно из наблюдений не является выбросом.
Стоит отметить, что в некоторых случаях исследователи считают наблюдения со стандартизованными остатками, превышающими абсолютное значение 2, выбросами.
Вам решать, использовать ли абсолютное значение 2 или 3 в качестве порога для выбросов, в зависимости от конкретной проблемы, над которой вы работаете.
Дополнительные ресурсы
Что такое остатки?
Что такое стандартизированные остатки?
Введение в множественную линейную регрессию