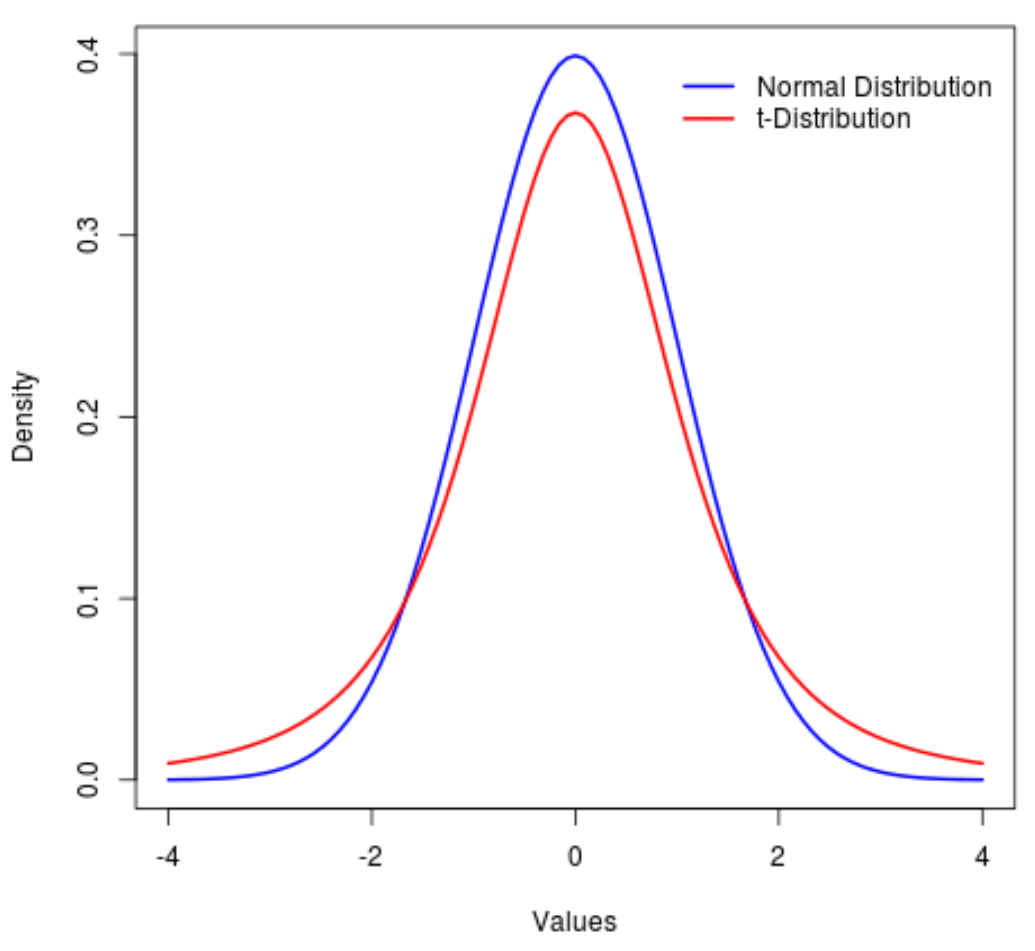
Распределение t — это распределение вероятностей, похожее на нормальное распределение , за исключением того, что у него более тяжелые «хвосты», чем у нормального распределения.
То есть больше значений в распределении находится в конце, чем в центре, по сравнению с нормальным распределением:
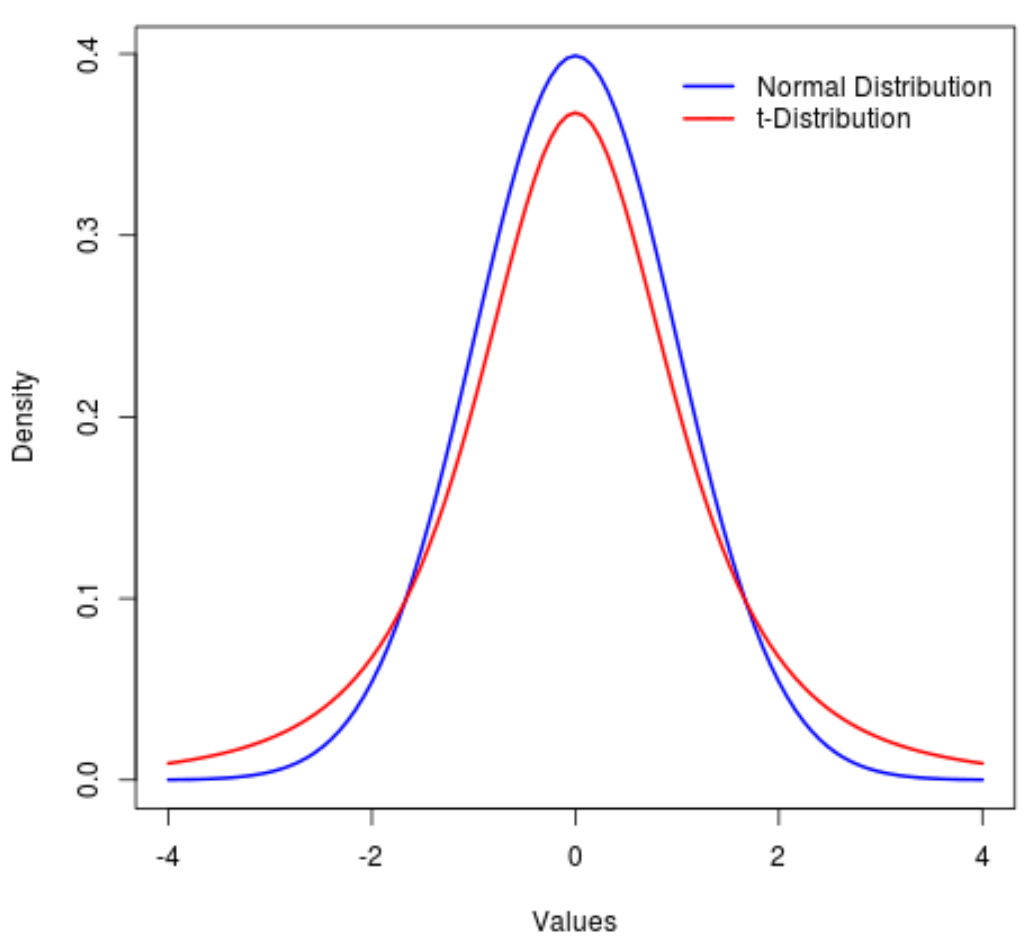
В этом руководстве объясняется, как использовать распределение t в Python.
Как генерировать при раздаче
Вы можете использовать функцию t.rvs(df, size) для генерации случайных значений из распределения at с определенными степенями свободы и размером выборки:
from scipy. stats import t
#generate random values from t distribution with df=6 and sample size=10
t. rvs (df= 6 , size= 10 )
array([-3.95799716, -0.01099963, -0.55953846, -1.53420055, -1.41775611,
-0.45384974, -0.2767931 , -0.40177789, -0.3602592 , 0.38262431])
В результате получается массив из 10 значений, следующих при распределении с 6 степенями свободы.
Как рассчитать P-значения, используя t-распределение
Мы можем использовать функцию t.cdf(x, df, loc=0, scale=1) , чтобы найти p-значение, связанное с некоторой статистикой t-теста.
Пример 1. Найдите одностороннее P-значение
Предположим, мы выполняем одностороннюю проверку гипотезы и в итоге получаем статистику проверки -1,5 и степени свободы = 10 .
Мы можем использовать следующий синтаксис для вычисления p-значения, соответствующего этой тестовой статистике:
from scipy. stats import t
#calculate p-value
t. cdf (x=-1.5, df=10)
0.08225366322272008
Одностороннее p-значение, соответствующее тестовой статистике -1,5 с 10 степенями свободы, равно 0,0822 .
Пример 2: найти двустороннее P-значение
Предположим, мы выполняем двустороннюю проверку гипотезы и в итоге получаем статистику теста 2,14 и степени свободы = 20 .
Мы можем использовать следующий синтаксис для вычисления p-значения, соответствующего этой тестовой статистике:
from scipy. stats import t
#calculate p-value
(1 - t. cdf (x=2.14, df=20)) \* 2
0.04486555082549959
Двустороннее p-значение, соответствующее тестовой статистике 2,14 с 20 степенями свободы, равно 0,0448 .
Примечание : Вы можете перепроверить эти ответы, используя Калькулятор обратного t-распределения .
Как строить планы при раздаче
Вы можете использовать следующий синтаксис для построения графика распределения с определенными степенями свободы:
from scipy. stats import t
import matplotlib.pyplot as plt
#generate t distribution with sample size 10000
x = t. rvs (df= 12 , size= 10000 )
#create plot of t distribution
plt.hist (x, density= True , edgecolor='black', bins= 20 )
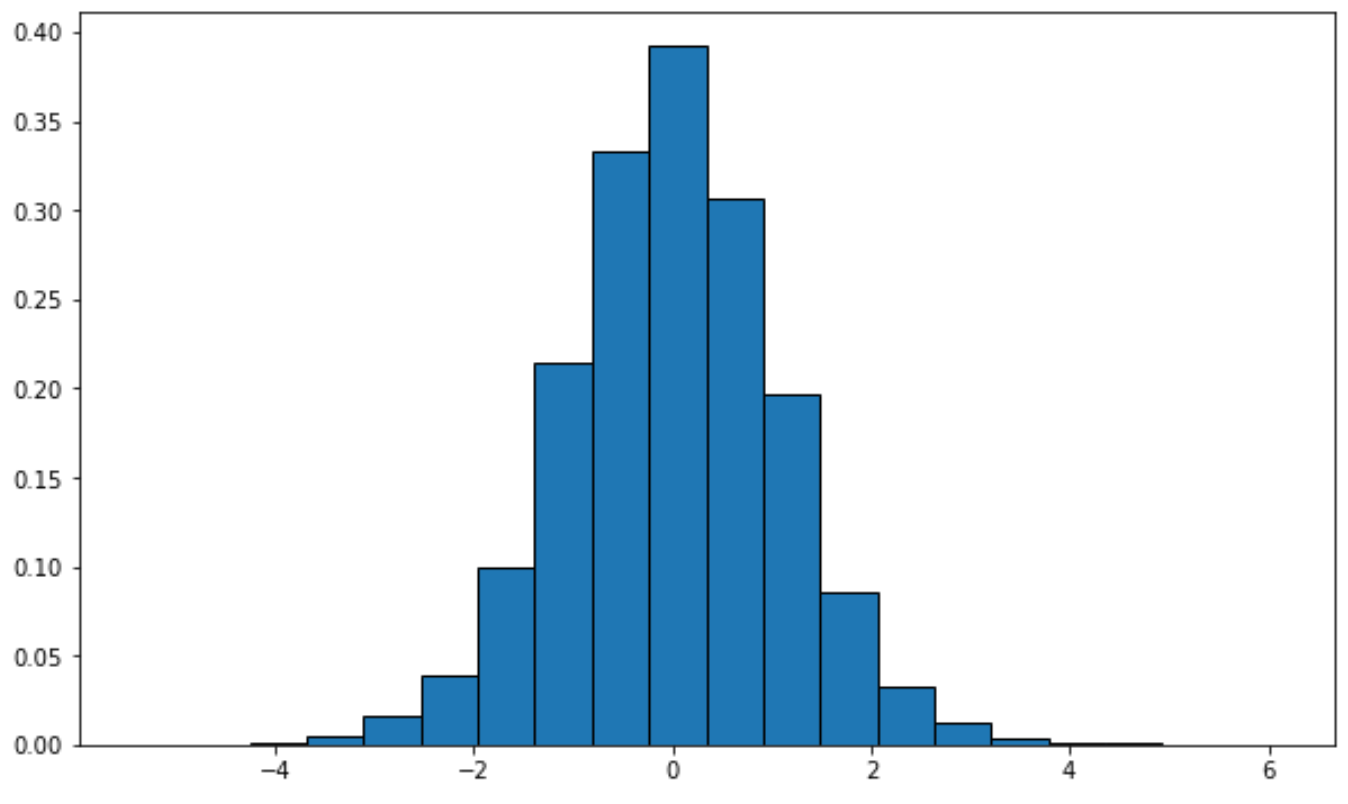
Кроме того, вы можете создать кривую плотности с помощью пакета визуализации Seaborn :
import seaborn as sns
#create density curve
sns.kdeplot (x)
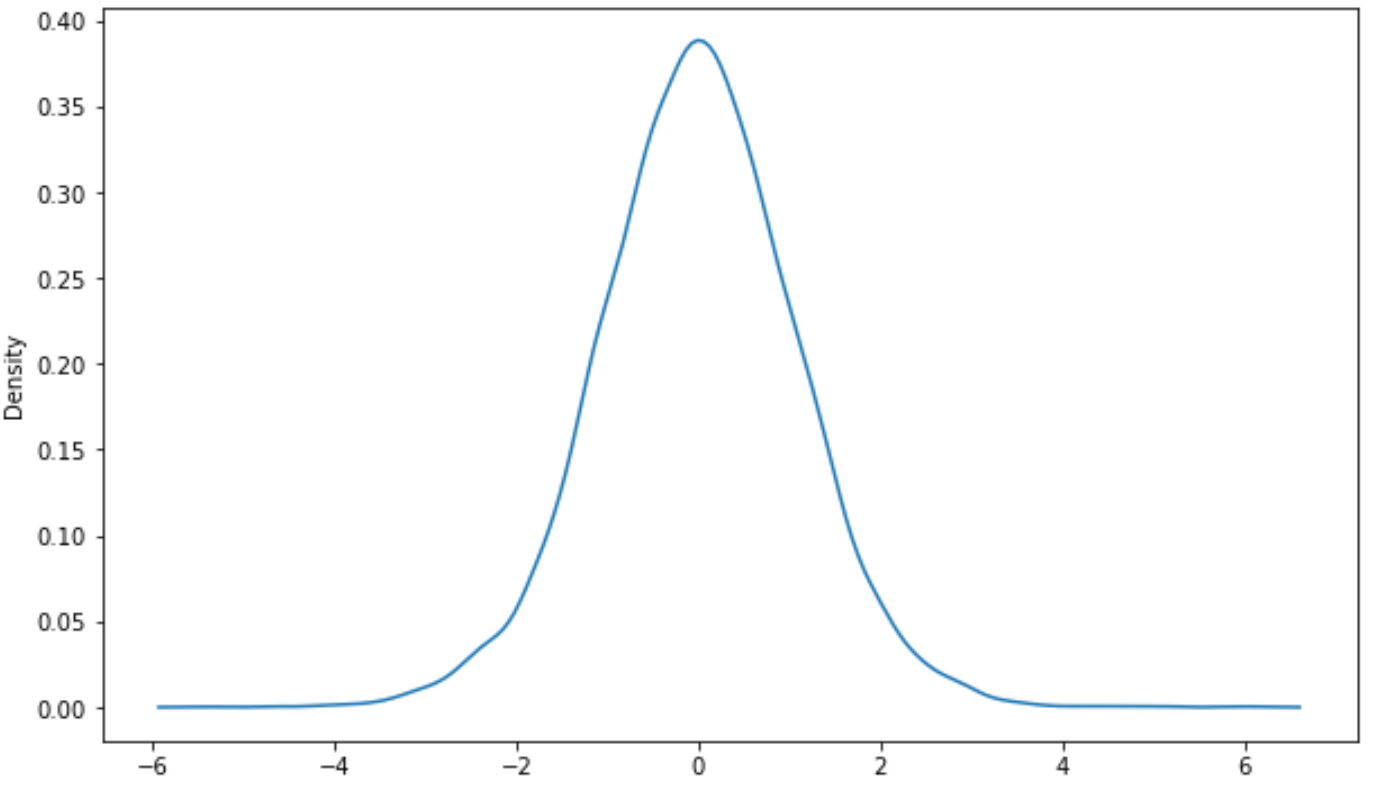
Дополнительные ресурсы
Следующие руководства предлагают дополнительную информацию о распределении t:
Нормальное распределение и t-распределение: в чем разница?
Калькулятор обратного t-распределения