Кривая плотности — это кривая на графике, представляющая распределение значений в наборе данных. Это полезно по трем причинам:
1. Кривая плотности дает нам хорошее представление о «форме» распределения, в том числе о том, имеет ли распределение один или несколько «пиков» часто встречающихся значений и имеет ли распределение наклон влево или вправо. .
2. Кривая плотности позволяет визуально увидеть, где находятся среднее значение и медиана распределения.
3. Кривая плотности позволяет визуально увидеть, какой процент наблюдений в наборе данных попадает между разными значениями.
Самая известная кривая плотности — это колоколообразная кривая, представляющая нормальное распределение .
Чтобы лучше понять кривые плотности, рассмотрим следующий пример.
Пример: создание и интерпретация кривой плотности
Предположим, у нас есть следующий набор данных, который показывает высоту 20 различных растений (в дюймах) на определенном поле:
4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2
Если бы мы создали простую гистограмму для отображения относительных частот каждого значения, она выглядела бы так:
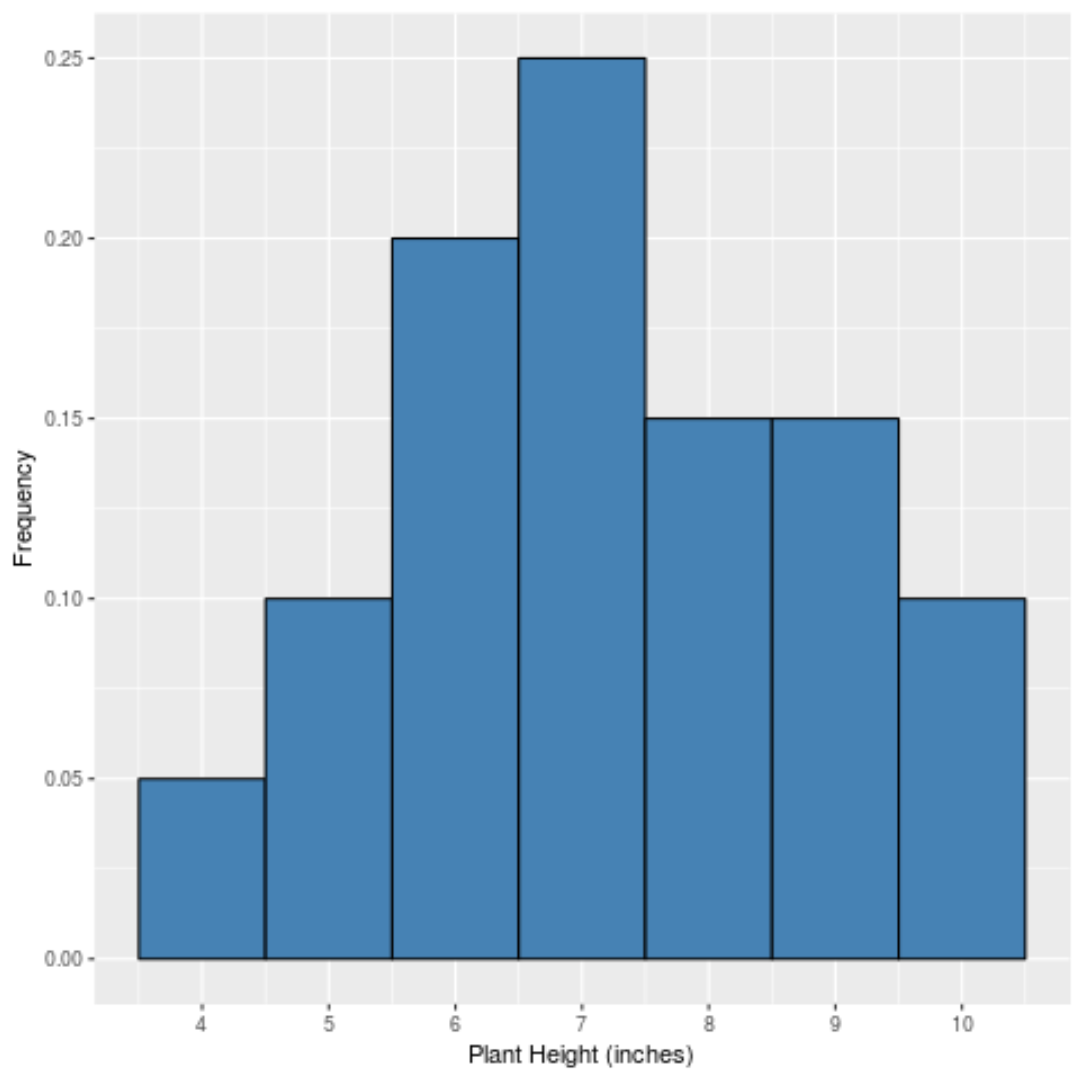
По оси X показано значение данных, а по оси Y — относительная частота (например, значение «7» встречается 5 раз из 20 всех значений в наборе данных, поэтому его относительная частота составляет 25% или 0,25 .
И если бы мы построили кривую плотности, чтобы зафиксировать «форму» этого распределения, она выглядела бы так:
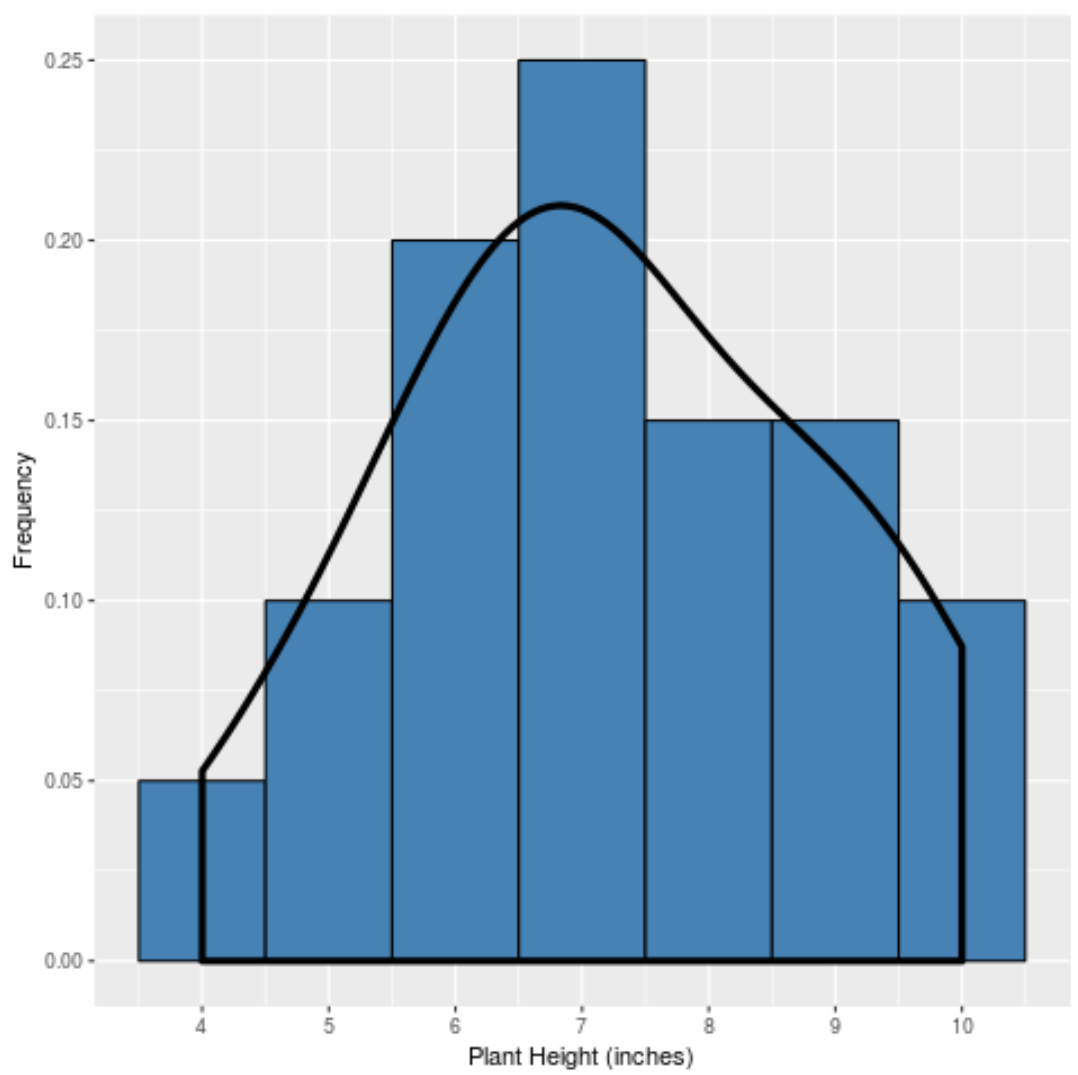
Кривая является самой высокой около центра распределения, потому что именно там находится наибольшее количество значений. Он также самый низкий ближе к концам распределения, потому что меньшее количество растений принимает эти значения (например, высота 4 дюйма или 10 дюймов).
Как интерпретировать кривые плотности
Кривые плотности бывают всех форм и размеров, и они позволяют нам получить быстрое визуальное представление о распределении значений в заданном наборе данных. В частности, они помогают нам визуализировать:
1. Асимметрия
Асимметрия — это способ описать симметрию распределения. Кривые плотности позволяют нам быстро увидеть, имеет ли график асимметрию влево, асимметрию вправо или отсутствие асимметрии:
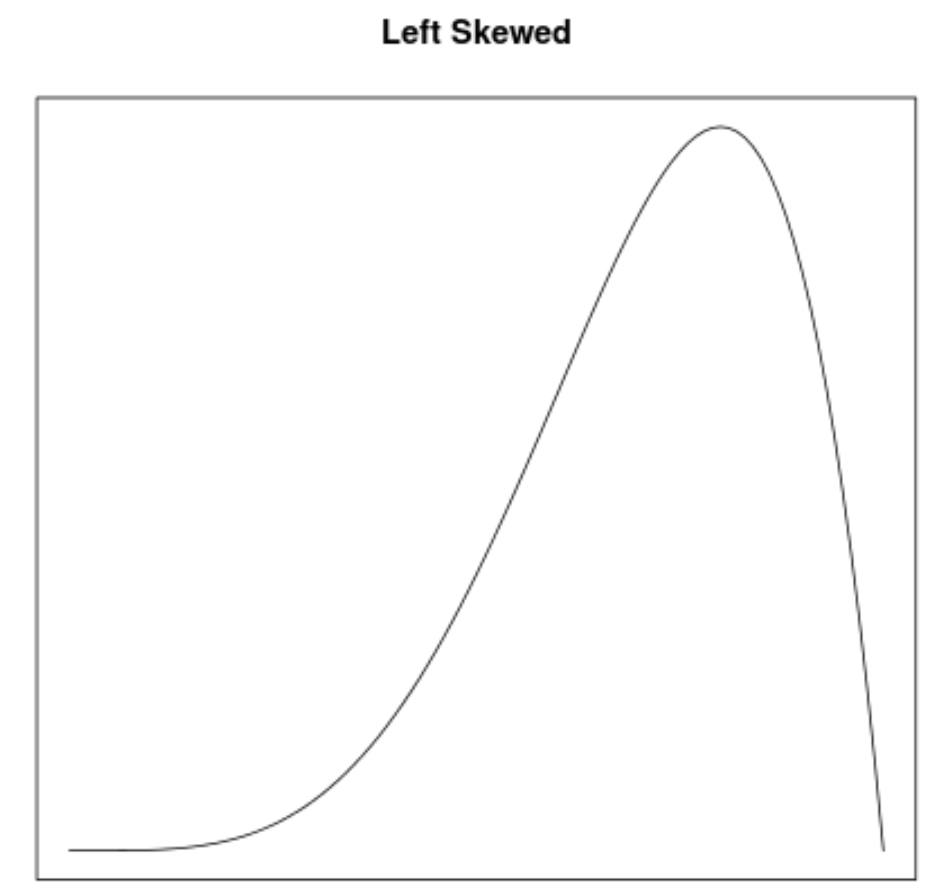
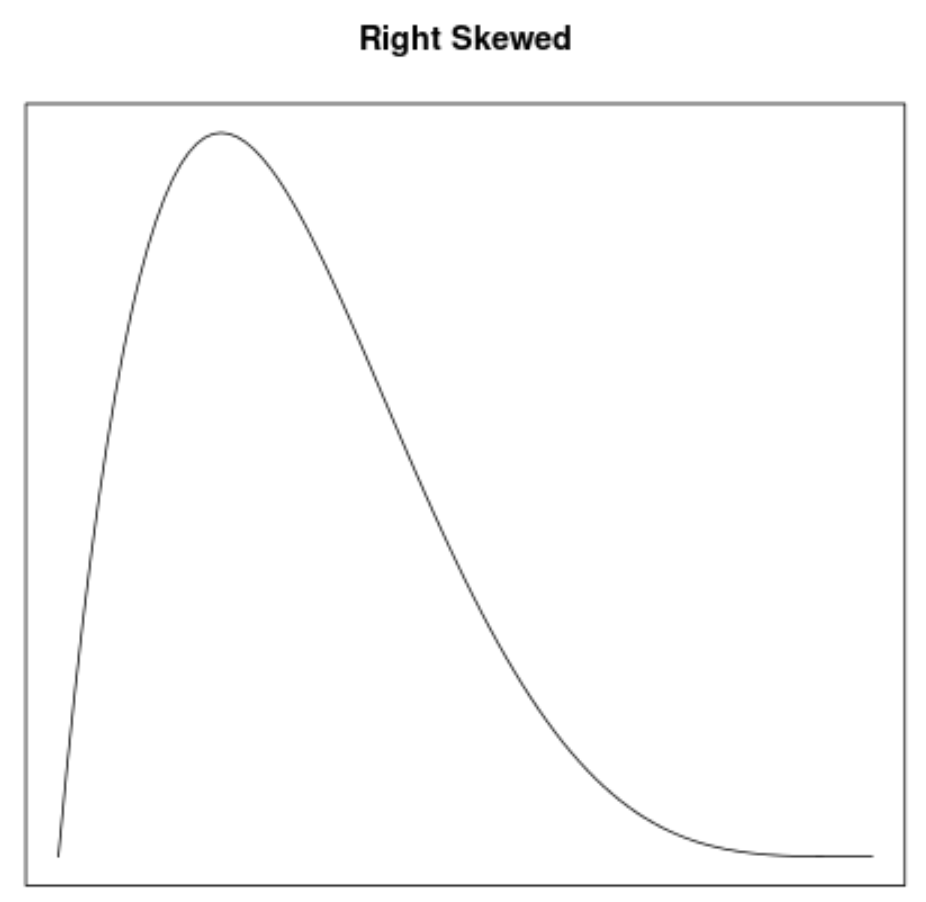
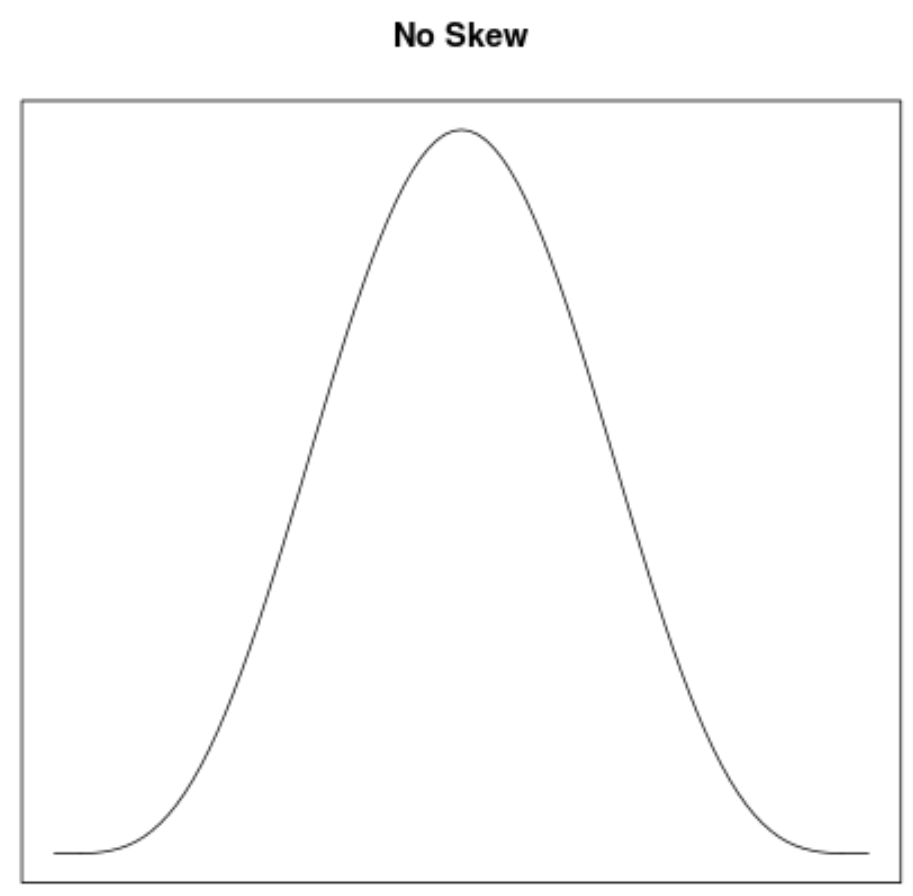
2. Расположение среднего и медианы
В зависимости от асимметрии кривой плотности мы можем быстро узнать, что больше в данном распределении: среднее или медиана. Особенно:
- Если кривая плотности наклонена влево , то среднее значение меньше медианы.
- Если кривая плотности наклонена вправо , то среднее значение больше медианы.
- Если кривая плотности не имеет перекоса , то среднее значение равно медиане.
3. Количество пиков
Кривые плотности также позволяют нам быстро увидеть, сколько «пиков» имеется в данном распределении. В каждом из приведенных выше примеров у распределений был только один пик, поэтому мы назвали бы эти распределения унимодальными .
Однако некоторые распределения могут иметь два пика, которые мы называембимодальными распределениями.И в редких случаях у нас также могут быть мультимодальные распределения с двумя или более пиками.
Просто создав кривую плотности для данного набора данных, мы можем быстро увидеть, сколько пиков в распределении.
Свойства кривых плотности
Кривые плотности обладают следующими свойствами:
- Площадь под кривой всегда составляет в сумме 100%.
- Кривая никогда не опустится ниже оси x.
Помните об этих двух фактах, когда создаете или интерпретируете кривые плотности для различных распределений.
Дополнительные ресурсы
Введение в гистограммы относительной частоты
Как сделать кривую нормального распределения в Excel
Как сделать кривую нормального распределения в Python