Критерий знакового ранга Уилкоксона — это непараметрическая версия t-критерия для парных выборок .
Он используется для проверки наличия существенной разницы между двумя средними значениями генеральной совокупности, когда распределение различий между двумя выборками нельзя считать нормальным .
В этом руководстве представлен пошаговый пример того, как провести знаковый ранговый тест Уилкоксона в Excel.
Шаг 1: Создайте данные
Предположим, инженер хочет знать, приводит ли новая обработка топлива к изменению среднего количества миль на галлон определенного автомобиля. Чтобы проверить это, он измеряет количество миль на галлон 12 автомобилей с обработкой топлива и без нее.
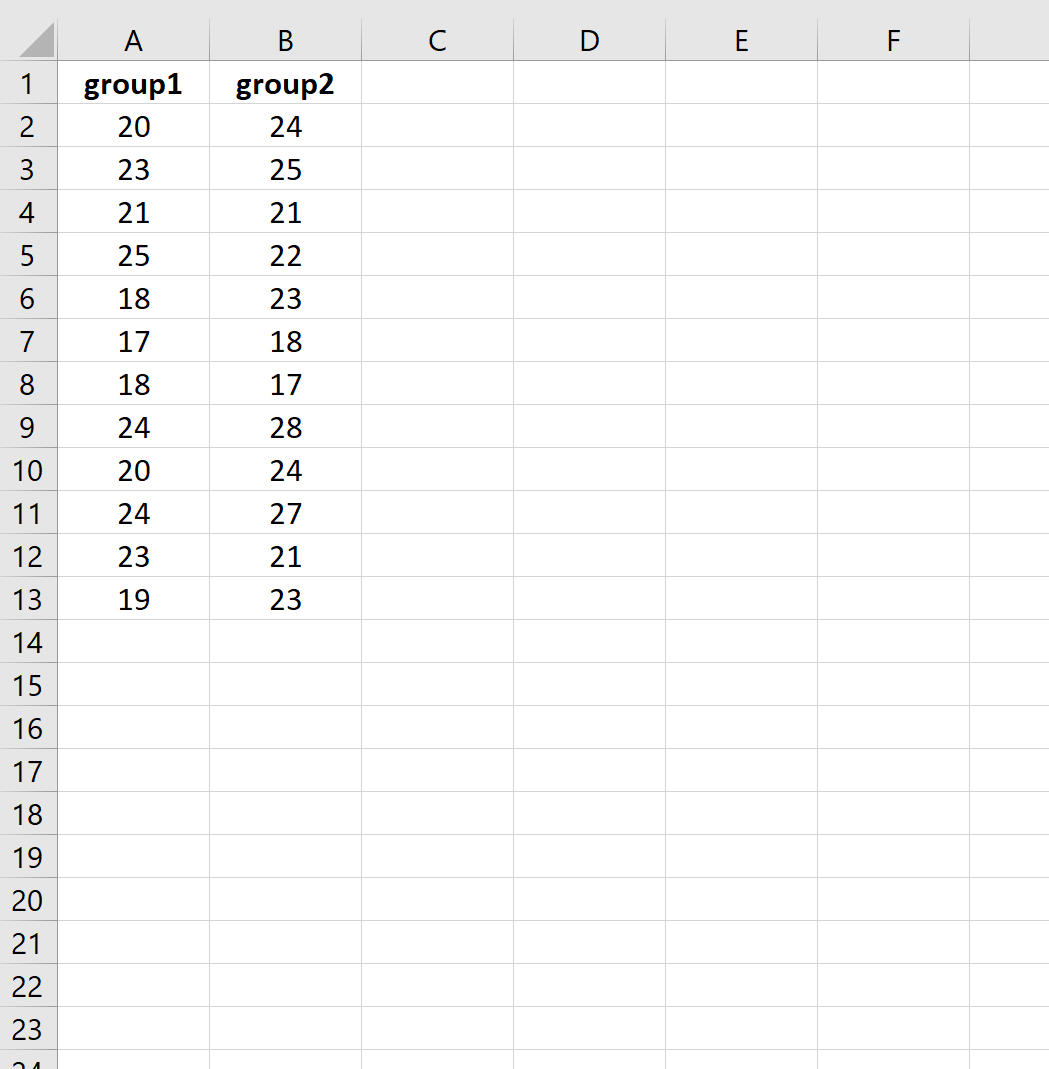
Мы создадим следующие данные в Excel, чтобы хранить значения миль на галлон для каждого автомобиля с обработкой топлива (группа 1) и без обработки топлива (группа 2):

Шаг 2: Рассчитайте разницу между группами
Далее посчитаем разницу между группами:

Шаг 3: Рассчитайте абсолютные разницы
Далее мы вычислим абсолютную разницу между группами, возвращая пустое значение, если абсолютная разница равна нулю:

Шаг 4: вычислить ранг абсолютных разностей
Далее мы будем использовать функцию RANK.AVG() для вычисления ранга абсолютной разницы между группами, возвращая пустое значение, если абсолютная разница равна нулю:

Шаг 5: Рассчитайте положительные и отрицательные ранги
Далее мы рассчитаем положительные ранги:

И посчитаем отрицательные ранги:

Шаг 6: Рассчитайте статистику теста и размер выборки
Наконец, мы вычислим тестовую статистику, которая просто меньше суммы положительных рангов или суммы отрицательных рангов:

И мы рассчитаем размер выборки, который представляет собой общее количество рангов, не равных нулю:
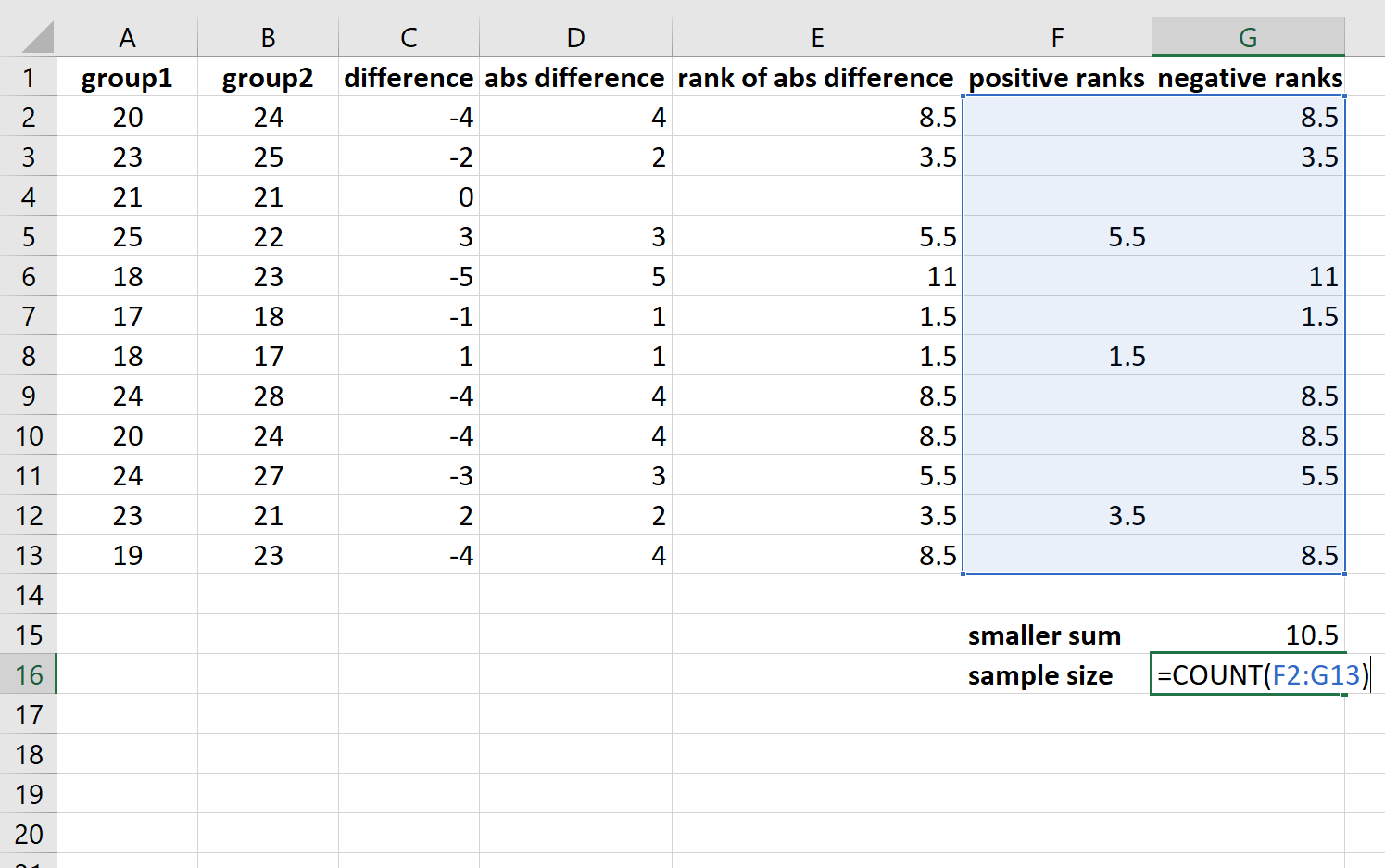
Тестовая статистика оказывается равной 10,5 , а размер выборки равен 11 .
В этом примере критерий знакового ранга Уилкоксона использует следующие нулевую и альтернативную гипотезы:
H 0 : миль на галлон равны между двумя группами
H A : Расход топлива в милях на галлон для двух групп неодинаков .
Чтобы определить, должны ли мы отклонить или не отклонить нулевую гипотезу, мы можем найти критическое значение, которое соответствует α = 0,05 и размеру выборки 11 в следующей таблице критических значений знакового рангового теста Уилкоксона:
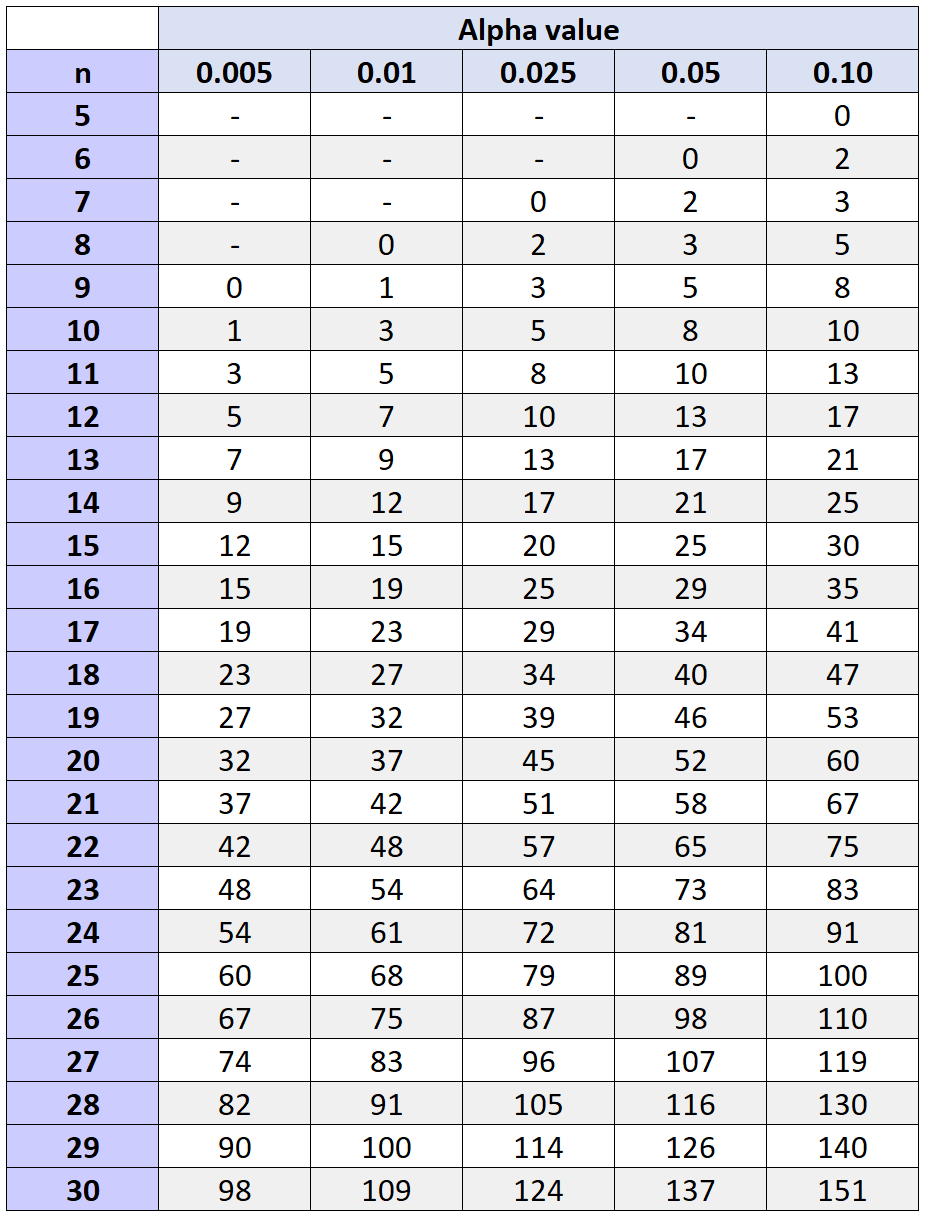
Критическое значение, соответствующее α = 0,05 и размеру выборки 11, равно 10 .
Поскольку тестовая статистика (10.5) не меньше критического значения 10, мы не можем отвергнуть нулевую гипотезу.
У нас нет достаточных доказательств, чтобы сказать, что средний расход топлива между двумя группами не одинаков.
Бонус: не стесняйтесь использовать этот калькулятор знакового рангового теста Уилкоксона для автоматического расчета статистики теста для знакового рангового теста Уилкоксона.