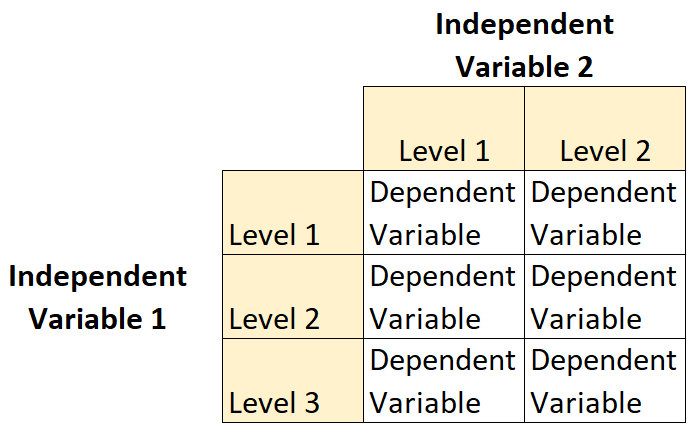
Факторный план 2×3 — это тип экспериментального плана, который позволяет исследователям понять влияние двух независимых переменных на одну зависимую переменную.
В этом типе плана одна независимая переменная имеет два уровня, а другая независимая переменная имеет три уровня.
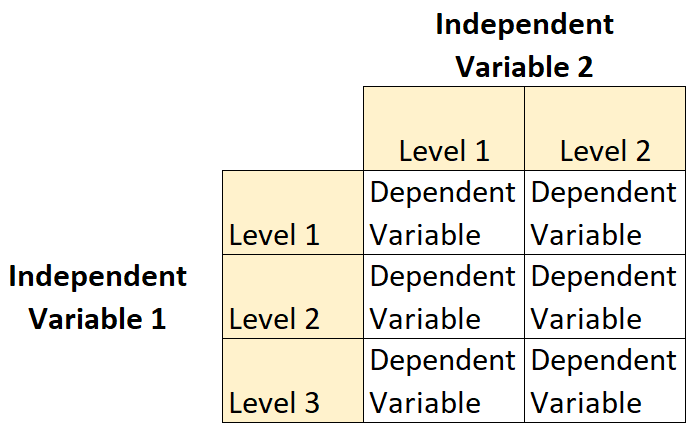
Например, предположим, что ботаник хочет понять влияние солнечного света (слабого, среднего или сильного) и частоты полива (ежедневного или еженедельного) на рост определенных видов растений.
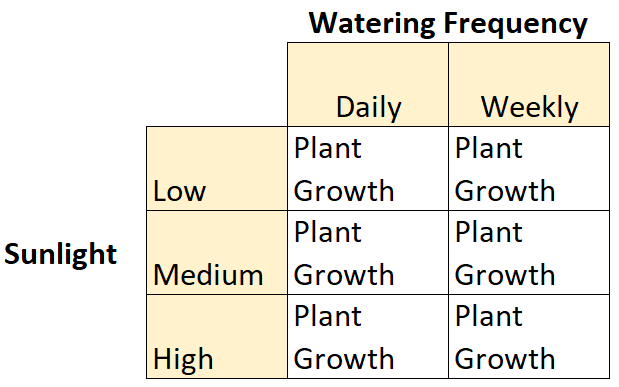
Это пример факторного плана 2 × 3, потому что есть две независимые переменные, одна из которых имеет два уровня, а другая — три уровня:
- Независимая переменная №1: Солнечный свет
- Уровни: низкий, средний, высокий
- Независимая переменная № 2: Частота полива.
- Уровни: Ежедневно, Еженедельно
И есть одна зависимая переменная: рост растений.
Цель факторного дизайна 2×3
Факторный план 2×3 позволяет анализировать следующие эффекты:
Основные эффекты: это эффекты, которые только одна независимая переменная оказывает на зависимую переменную.
Например, в нашем предыдущем сценарии мы могли проанализировать следующие основные эффекты:
- Основное влияние солнечного света на рост растений.
- Средний рост всех растений, получавших мало солнечного света.
- Средний рост всех растений, получавших средний солнечный свет.
- Средний рост всех растений, получавших много солнечного света.
- Основное влияние частоты полива на рост растений.
- Средний рост всех растений, которые поливали ежедневно.
- Средний рост всех растений, которые поливали еженедельно.
Эффекты взаимодействия: они возникают, когда эффект, который одна независимая переменная оказывает на зависимую переменную, зависит от уровня другой независимой переменной.
Например, в нашем предыдущем сценарии мы могли проанализировать следующие эффекты взаимодействия:
- Зависит ли влияние солнечного света на рост растений от частоты полива?
- Зависит ли влияние частоты полива на рост растений от количества солнечного света?
Как анализировать факторный план 2×3
Мы можем выполнить двусторонний ANOVA , чтобы формально проверить, имеют ли независимые переменные статистически значимую связь с зависимой переменной.
Например, следующий код показывает, как выполнить двусторонний ANOVA для нашего гипотетического сценария завода в R:
#make this example reproducible
set. seed (0)
#create data
df <- data.frame(sunlight = rep(c('Low', 'Medium', 'High'), each = 15, times = 2),
water = rep(c('Daily', 'Weekly'), each = 45, times = 2),
growth = c(rnorm(15, 9, 2), rnorm(15, 10, 3), rnorm(15, 13, 2),
rnorm(15, 8, 3), rnorm(15, 10, 4), rnorm(15, 12, 3)))
#fit the two-way ANOVA model
model <- aov(growth ~ sunlight \* water, data = df)
#view the model output
summary(model)
Df Sum Sq Mean Sq F value Pr(>F)
sunlight 2 602.3 301.15 50.811 <2e-16 \*\*\*
water 1 39.6 39.62 6.685 0.0105 \*
sunlight:water 2 15.1 7.56 1.275 0.2819
Residuals 174 1031.3 5.93
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Вот как интерпретировать результат ANOVA:
- Значение p, связанное с солнечным светом, составляет <2e-16.Поскольку это меньше 0,05, это означает, что воздействие солнечного света оказывает статистически значимое влияние на рост растений.
- Значение p, связанное с водой, составляет 0,0105.Поскольку этот показатель меньше 0,05, это означает, что частота полива также оказывает статистически значимое влияние на рост растений.
- Значение p для взаимодействия между солнечным светом и водой составляет 0,2819.Поскольку это не менее 0,05, это означает, что между солнечным светом и водой нет эффекта взаимодействия.
Дополнительные ресурсы
В следующих учебных пособиях представлена дополнительная информация о планировании эксперимента и анализе:
Полное руководство: факторный дизайн 2×2
Что такое уровни независимой переменной?
Независимые и зависимые переменные
Что такое факториальный дисперсионный анализ?