Биномиальное распределение в статистике описывает вероятность достижения k успехов в n испытаниях, когда вероятность успеха в одном эксперименте равна p .
Чтобы рассчитать вероятности биномиального распределения в Google Таблицах, мы можем использовать функцию БИНОМРАСП , которая использует следующий базовый синтаксис:
БИНОМРАСП(k, n, p, совокупный)
куда:
- k : Количество успехов
- n : количество испытаний
- p : Вероятность успеха в данном испытании
- cumulative : вычислять ли кумулятивную вероятность (по умолчанию FALSE)
В следующих примерах показано, как использовать эту функцию на практике.
Пример 1: Вероятность ровно k успехов
Тай делает 60% своих штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он сделает ровно 10?
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Google Таблицах:
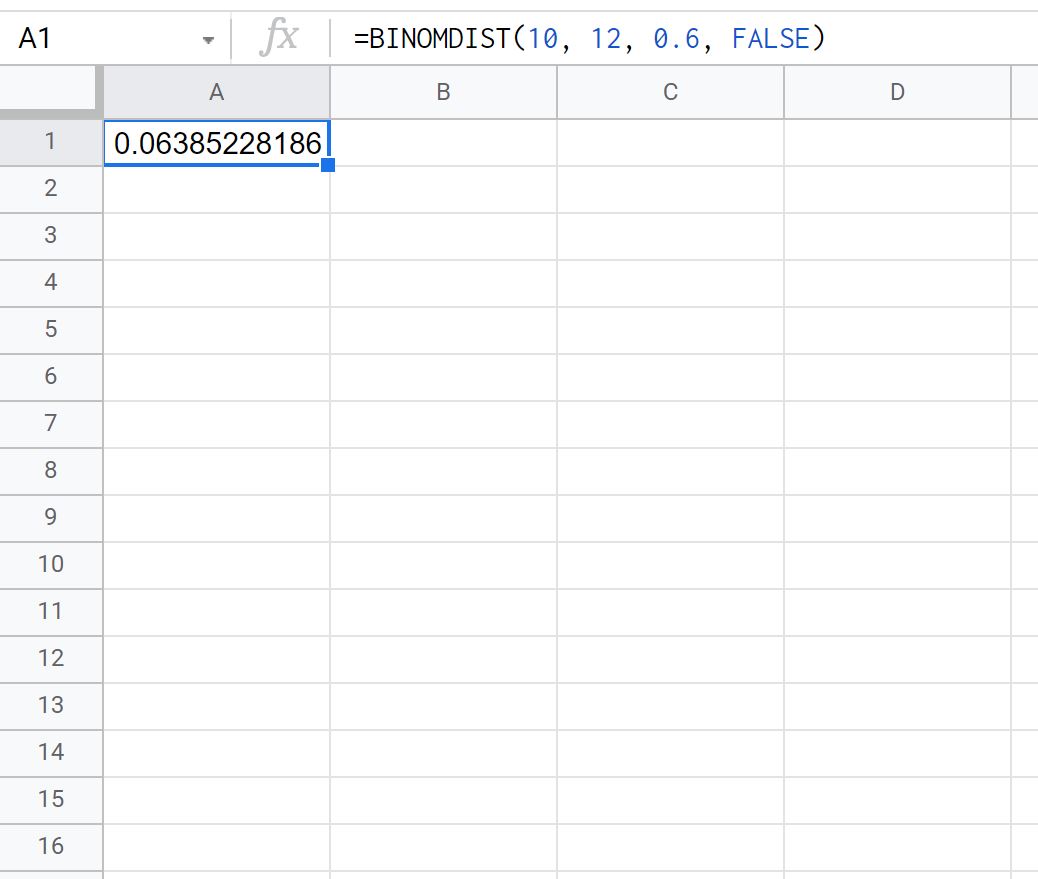
= BINOMDIST ( 10 , 12 , 0.6 , FALSE )
На следующем снимке экрана показано, как использовать эту формулу на практике:
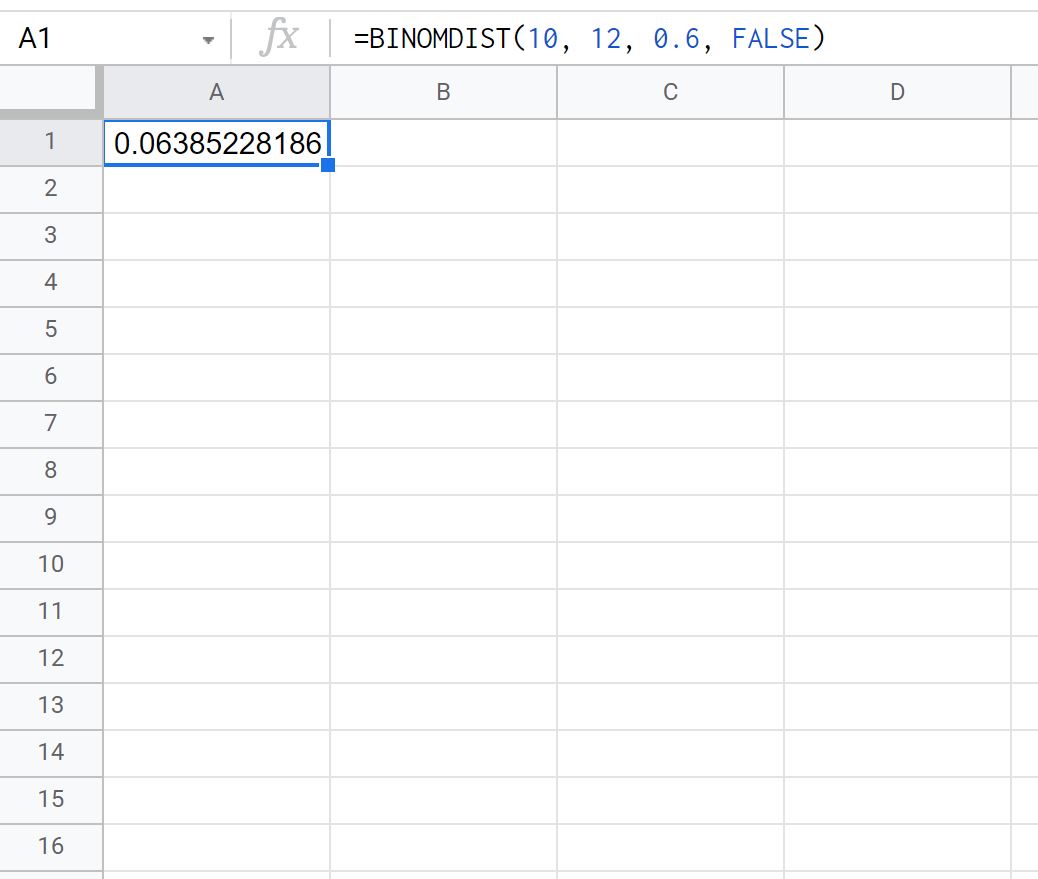
Вероятность того, что Тай выполнит ровно 10 штрафных бросков из 12, равна 0,0639 .
Пример 2: Вероятность менее чем k успехов
Тай делает 60% своих штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он сделает меньше 10?
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Google Таблицах:
= BINOMDIST ( 9 , 12 , 0.6 , TRUE )
На следующем снимке экрана показано, как использовать эту формулу на практике:
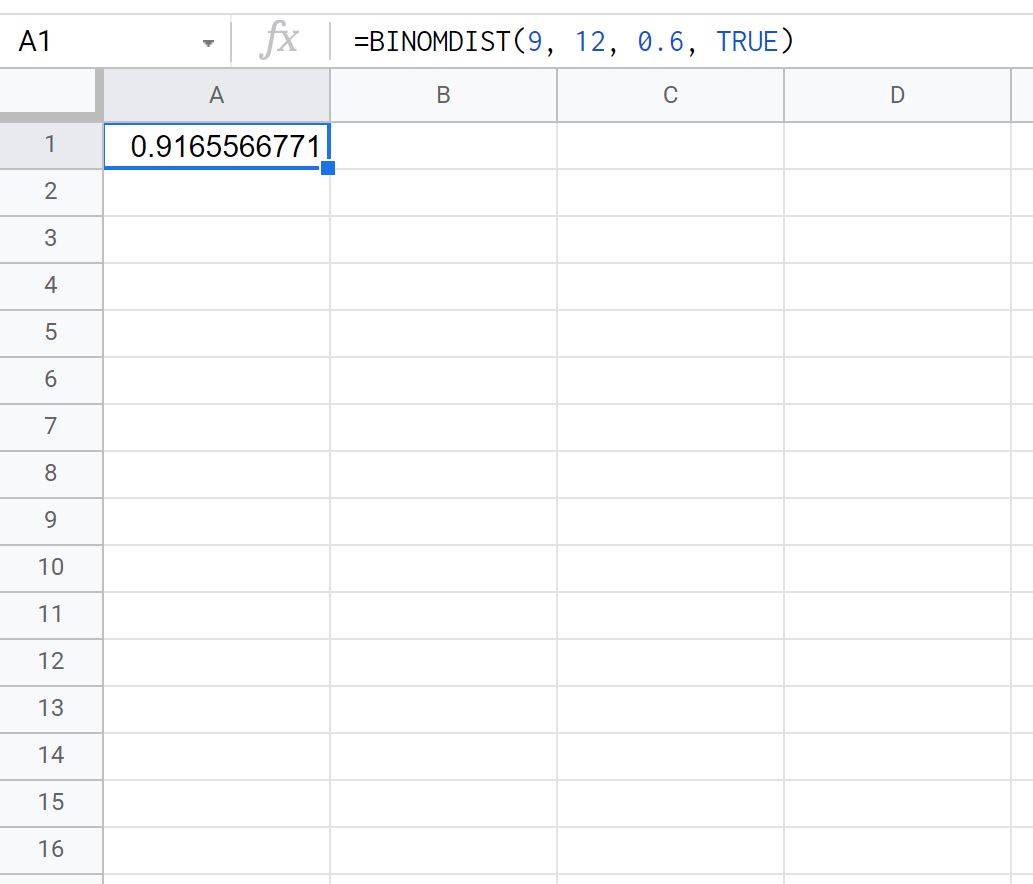
Вероятность того, что Тай сделает менее 10 попыток штрафного броска из 12, равна 0,9166 .
Пример 3: Вероятность меньше или равна k успехов
Тай делает 60% своих штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он сделает меньше или равно 10?
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Google Таблицах:
= BINOMDIST ( 10 , 12 , 0.6 , TRUE )
На следующем снимке экрана показано, как использовать эту формулу на практике:
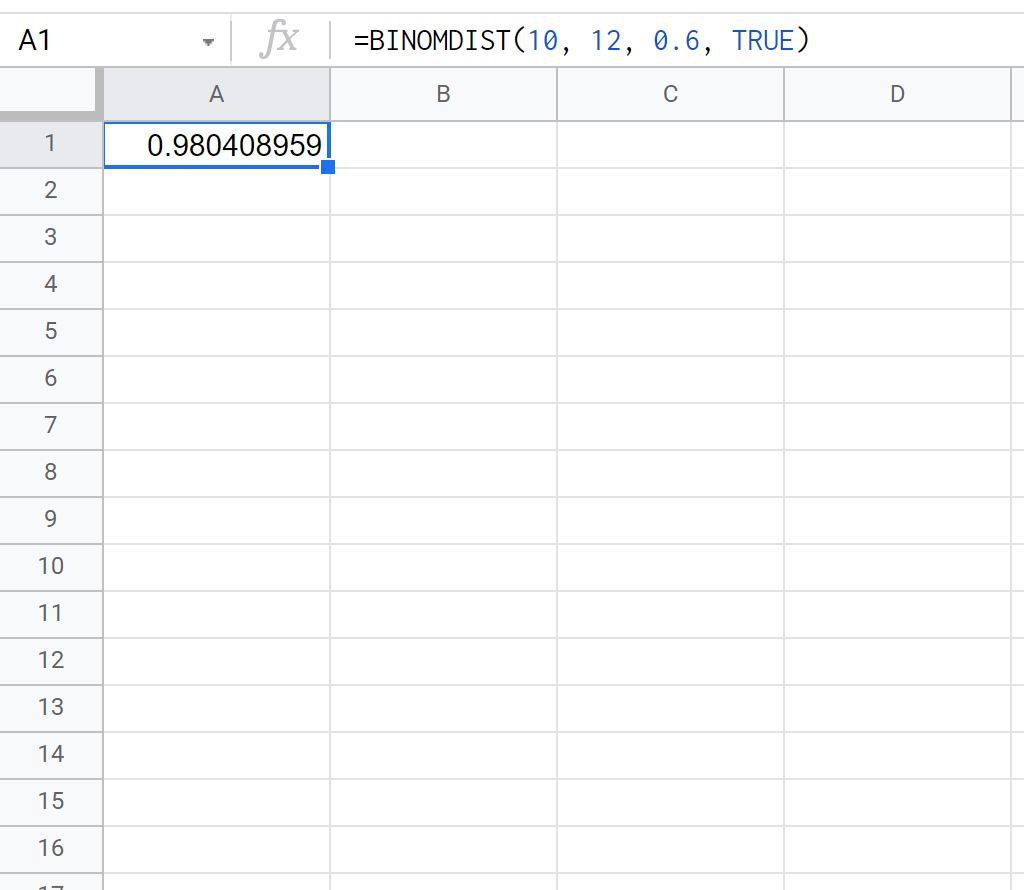
Вероятность того, что Тай совершит меньше или равно 10 штрафных бросков из 12, равна 0,9166 .
Пример 4: Вероятность более чем k успехов
Тай делает 60% своих штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он сделает больше 10?
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Google Таблицах:
=1- BINOMDIST ( 10 , 12 , 0.6 , TRUE )
На следующем снимке экрана показано, как использовать эту формулу на практике:
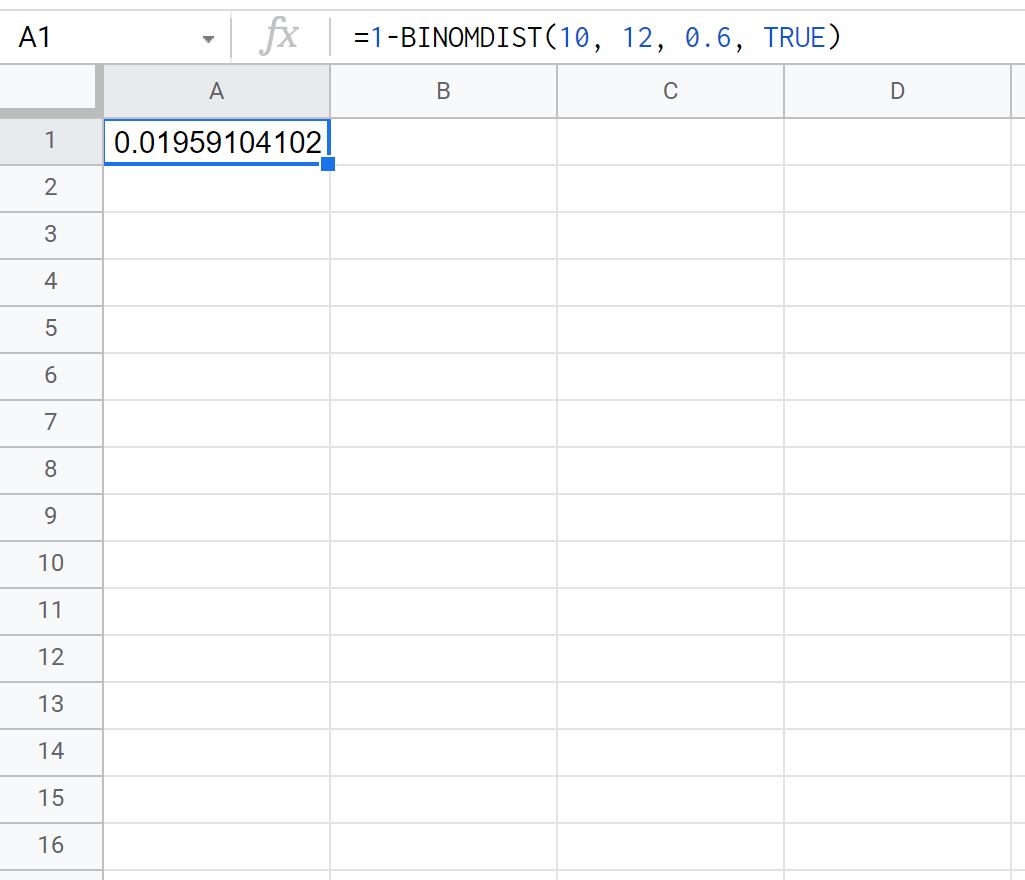
Вероятность того, что Тай совершит более 10 штрафных бросков из 12, равна 0,0196 .
Пример 5: Вероятность успеха больше или равна k
Тай делает 60% своих штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он сделает больше или равно 10?
Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Google Таблицах:
=1- BINOMDIST ( 9 , 12 , 0.6 , TRUE )
На следующем снимке экрана показано, как использовать эту формулу на практике:
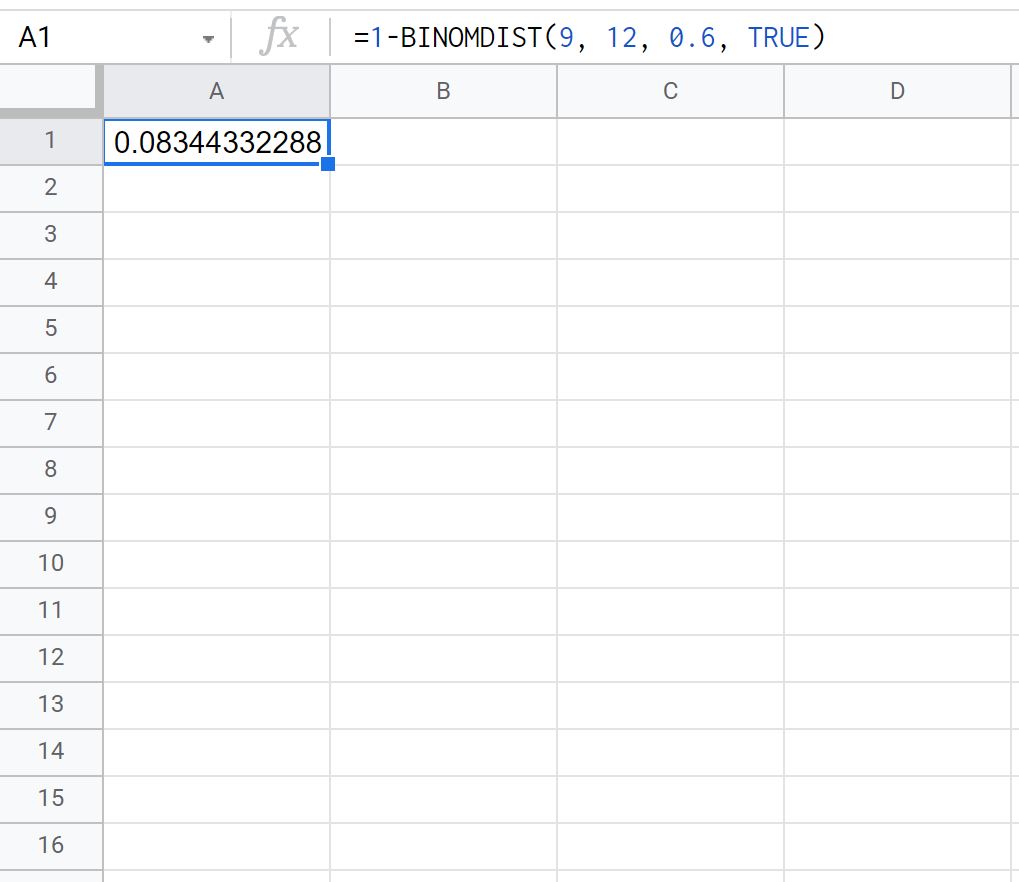
Вероятность того, что Тай сделает больше или равно 10 штрафных бросков из 12, равна 0,0834 .
Бонус : вы можете использовать калькулятор биномиального распределения для автоматического расчета биномиальных вероятностей для любых значений n , k и p .
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о биномиальном распределении:
Введение в биномиальное распределение
Три допущения биномиального распределения
5 реальных примеров биномиального распределения