Преобразование Бокса-Кокса — это широко используемый метод преобразования ненормально распределенного набора данных в более нормально распределенный .
Основная идея этого метода состоит в том, чтобы найти некоторое значение λ, чтобы преобразованные данные были как можно ближе к нормальному распределению, используя следующую формулу:
- y(λ) = (y λ – 1) / λ, если y ≠ 0
- y(λ) = log(y), если y = 0
Мы можем выполнить преобразование box-cox в R, используя функцию boxcox() из библиотеки MASS().В следующем примере показано, как использовать эту функцию на практике.
Обратитесь к этой статье из Университета Коннектикута за хорошим кратким изложением развития преобразования Бокса-Кокса.
Пример: преобразование Бокса-Кокса в R
В следующем коде показано, как подобрать модель линейной регрессии к набору данных, а затем использовать функцию boxcox() , чтобы найти оптимальную лямбду для преобразования переменной ответа и соответствия новой модели.
library (MASS)
#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)
#fit linear regression model
model <- lm(y~x)
#find optimal lambda for Box-Cox transformation
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])
[1] -0.4242424
#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)
Оптимальная лямбда оказалась равной -0,4242424.Таким образом, новая регрессионная модель заменила исходную переменную отклика y на переменную y = (y -0,4242424 – 1) / -0,4242424.
В следующем коде показано, как создать два графика QQ в R, чтобы визуализировать различия в остатках между двумя моделями регрессии:
#define plotting area
op <- par(pty = "s", mfrow = c(1, 2))
#Q-Q plot for original model
qqnorm(model$residuals)
qqline(model$residuals)
#Q-Q plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)
#display both Q-Q plots
par(op)
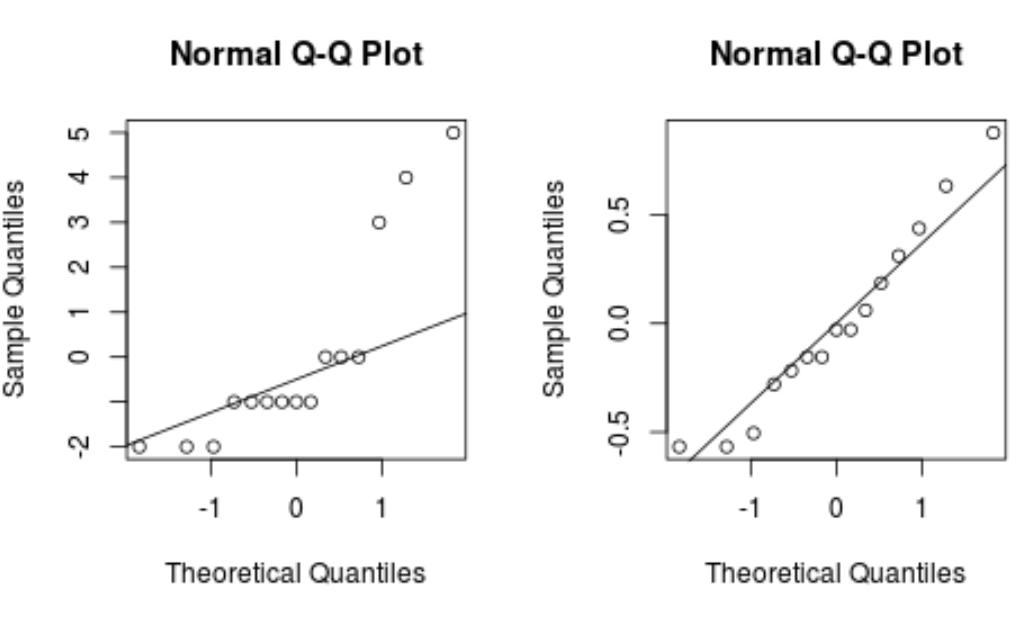
Как правило, если точки данных падают на прямую диагональную линию на графике QQ, то набор данных, вероятно, следует нормальному распределению.
Обратите внимание, как модель преобразования Бокса-Кокса создает график QQ с гораздо более прямой линией, чем исходная модель регрессии.
Это указывает на то, что остатки модели, преобразованной по боксу-коксу, распределяются гораздо более нормально, что удовлетворяет одному из предположений линейной регрессии .
Дополнительные ресурсы
Как преобразовать данные в R (логарифм, квадратный корень, кубический корень)
Как создать и интерпретировать график QQ в R
Как выполнить тест Шапиро-Уилка на нормальность в R