Простая линейная регрессия используется для количественной оценки взаимосвязи между переменной-предиктором и переменной-ответом.
Этот метод находит строку, которая лучше всего «соответствует» набору данных, и принимает следующий вид:
ŷ = б 0 + б 1 х
куда:
- ŷ : Расчетное значение отклика
- b 0 : точка пересечения линии регрессии
- b 1 : Наклон линии регрессии
- x : значение переменной-предиктора
Часто нас интересует значение b 1 , которое сообщает нам среднее изменение переменной отклика , связанное с увеличением на одну единицу переменной предиктора.
Мы можем использовать следующую формулу для расчета доверительного интервала для значения β 1 , значения наклона для генеральной совокупности:
Доверительный интервал для β 1 : b 1 ± t 1-α/2, n-2 * se(b 1 )
куда:
- b 1 = коэффициент наклона, показанный в таблице регрессии
- t 1-∝/2, n-2 = критическое значение t для доверительного уровня 1-∝ с n-2 степенями свободы, где n — общее количество наблюдений в нашем наборе данных
- se(b 1 ) = стандартная ошибка b 1 , показанная в таблице регрессии
В следующем примере показано, как на практике рассчитать доверительный интервал для наклона регрессии.
Пример: доверительный интервал для наклона регрессии
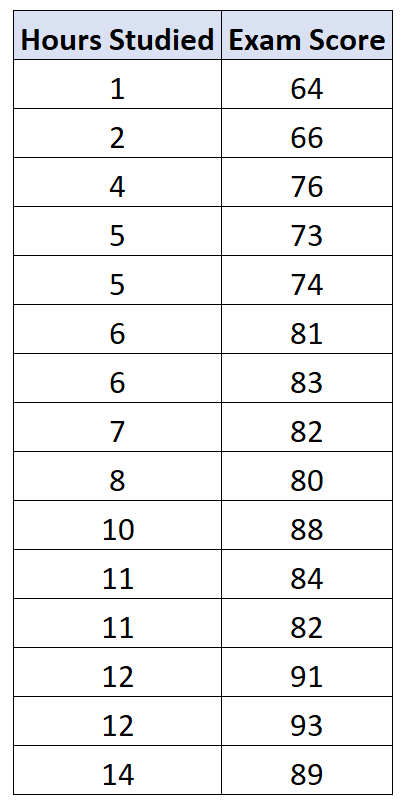
Предположим, мы хотим подогнать простую модель линейной регрессии, используя часы обучения в качестве переменной-предиктора и баллы за экзамены в качестве переменной-ответа для 15 учеников в конкретном классе:

Мы можем выполнить простую линейную регрессию в Excel и получить следующий результат:

Используя оценки коэффициентов в выходных данных, мы можем записать подобранную простую модель линейной регрессии как:
Оценка = 65,334 + 1,982 * (часы обучения)
Значение наклона регрессии равно 1,982 .
Это говорит нам о том, что каждый дополнительный час обучения связан со средним увеличением экзаменационного балла на 1,982 .
Мы можем использовать следующую формулу для расчета 95% доверительного интервала для перехвата:
- 95% ДИ для β 1 : b 1 ± t 1-α/2, n-2 * se(b 1 )
- 95% ДИ для β 1 : 1,982 ± t 0,975, 15-2 * 0,248
- 95% ДИ для β 1 : 1,982 ± 2,1604 * 0,248
- 95% ДИ для β 1 : [1,446, 2,518]
95% доверительный интервал для наклона регрессии составляет [1,446, 2,518] .
Поскольку этот доверительный интервал не содержит значения 0, мы можем заключить, что существует статистически значимая связь между отработанными часами и экзаменационной оценкой.
Примечание.Мы использовали Калькулятор обратного распределения t , чтобы найти критическое значение t, соответствующее 95% доверительному уровню с 13 степенями свободы.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о линейной регрессии:
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Как читать и интерпретировать таблицу регрессии
Как сообщить о результатах регрессии