Распределение Эрланга — этораспределение вероятностей, первоначально созданное AK Erlang для моделирования количества телефонных звонков, которые может принять оператор на коммутационной станции одновременно.
Распределение используется в инженерии телефонного трафика, системах массового обслуживания, математической биологии и других областях для моделирования различных явлений реального мира.
Свойства распределения Эрланга
Распределение Эрланга имеет следующую функцию плотности вероятности:
f(x; k, µ) = x k-1 e -x/µ / µ k (k-1)!
куда:
- k: Параметр формы. Это должно быть положительное целое число.
- μ: Параметр масштаба. Это должно быть положительное действительное число.
Оказывается, распределение Эрланга — это частный случай гамма-распределения, когда параметр формы k ограничен только положительными целыми числами.
Обратите внимание, что параметр масштаба является величиной, обратной величине параметра скорости, λ, т. е. μ = 1/λ.
Распределение Эрланга обладает следующими свойствами:
- Среднее значение: к/λ
- Режим: (k-1)/λ
- Дисперсия: k/λ 2
- Асимметрия: 2/√k
- Эксцесс: 6/k
Распределение Erlang имеет следующие отношения с другими дистрибутивами:
- Когда параметр формы k равен 1, распределение Эрланга равно экспоненциальному распределению .
- Когда параметр масштаба μ равен 2, распределение Эрланга равно распределению хи-квадрат с 2 степенями свободы.
Визуализация распределения Эрланга
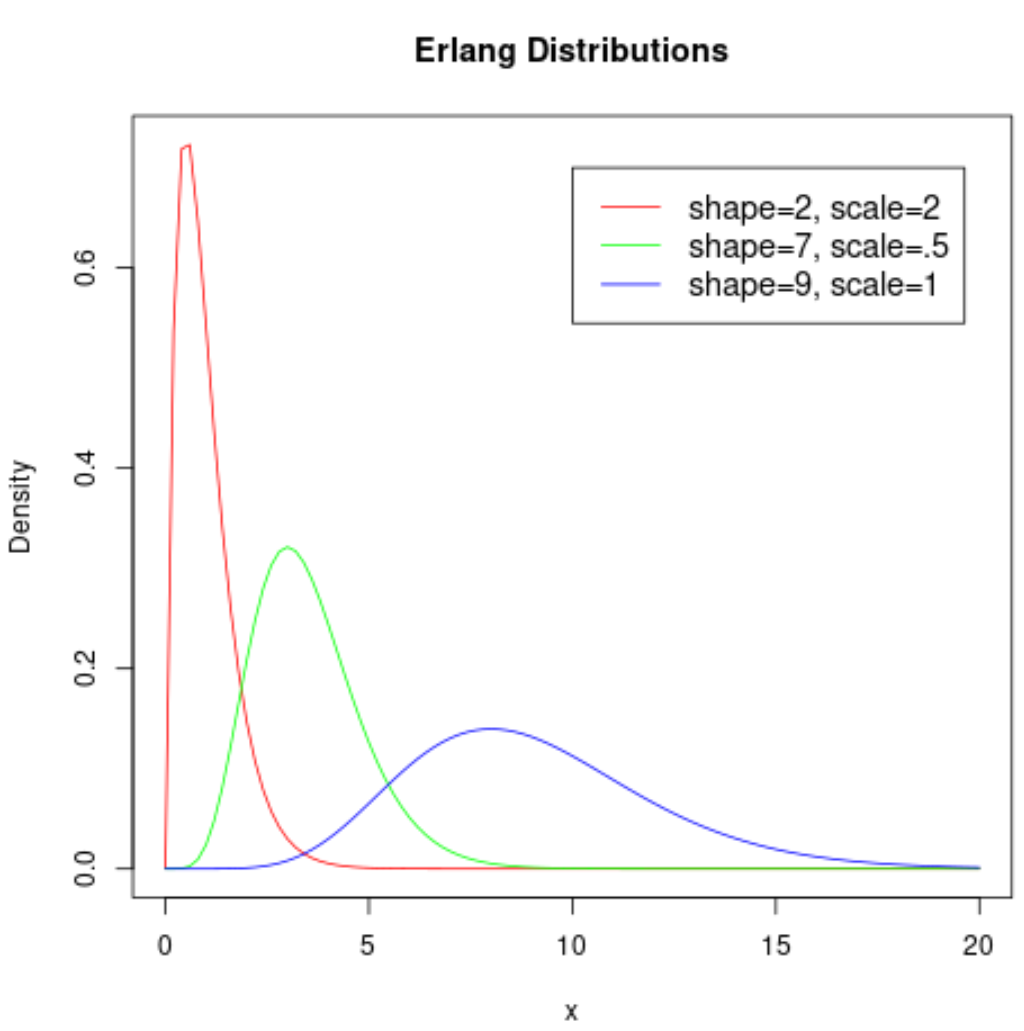
На следующем графике показана форма распределения Эрланга при различных параметрах:
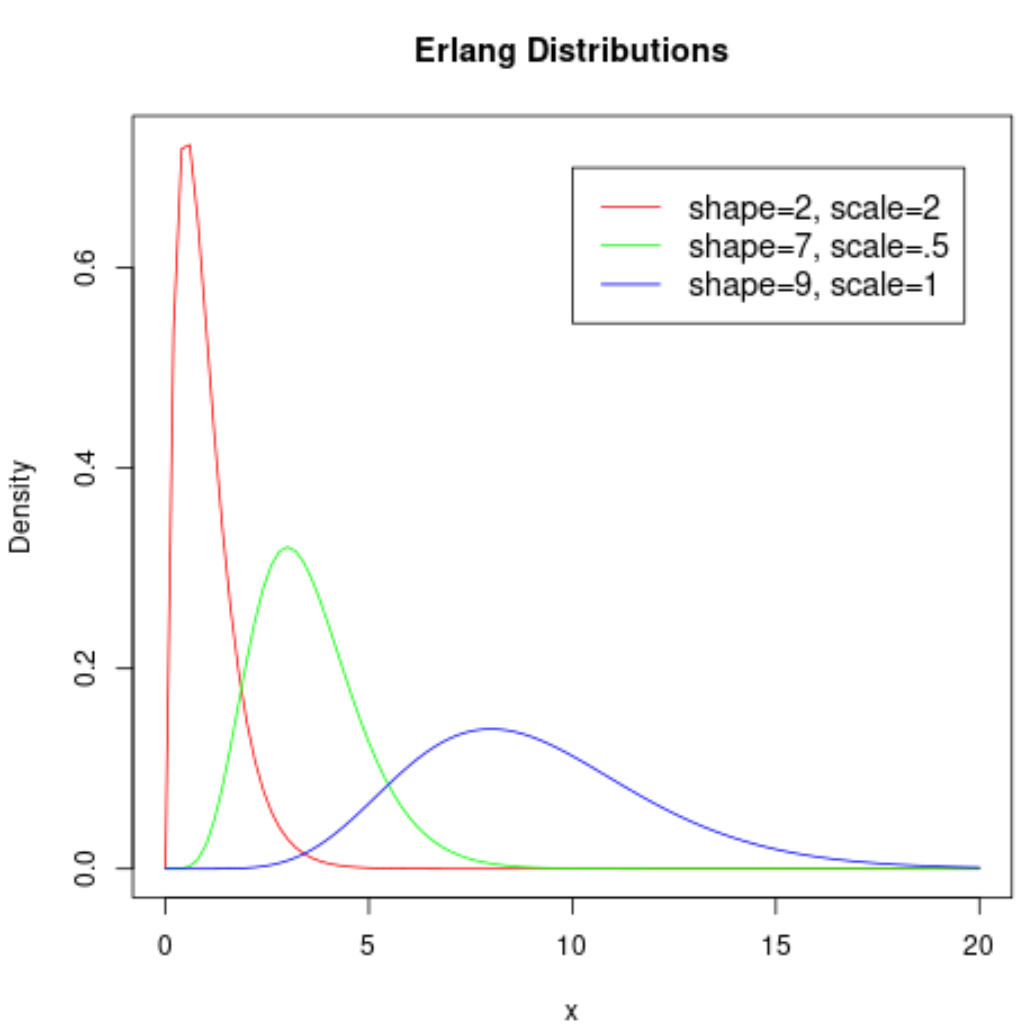
Интересно посмотреть, насколько форма распределения меняется в зависимости от значений, используемых для параметров формы и масштаба.
Примечание. Вы можете найти код R, используемый для генерации графика распределений Эрланга, здесь .
Сценарии использования
Распределение Erlang используется в различных реальных условиях, включая:
1. Колл-центры
Распределение Эрланга используется для моделирования времени между входящими вызовами в колл-центр вместе с ожидаемым количеством вызовов.
Это позволяет колл-центрам знать, какой должна быть их кадровая мощность в разное время дня, чтобы они могли своевременно обрабатывать входящие звонки, не теряя денег из-за набора слишком большого количества сотрудников в течение данной смены.
2. Медицинские настройки
Распределение Эрланга широко используется для моделирования распределения времени клеточного цикла, которое имеет множество различных применений в медицинских учреждениях.
3. Розничные настройки
Распределение Эрланга используется розничными торговцами для моделирования частоты повторных покупок потребителями.
Это дает розничным торговцам и другим предприятиям представление о том, как часто данный потребитель будет покупать у них продукт или услугу. Это помогает предприятиям с контролем запасов, а также с персоналом.
Дополнительные ресурсы
Введение в нормальное распределение
Введение в биномиальное распределение
Введение в распределение Пуассона