Геометрическое распределение описывает вероятность испытать определенное количество неудач, прежде чем испытать первый успех в серии испытаний Бернулли.
Испытание Бернулли — это эксперимент с двумя возможными исходами — «успех» или «неудача» — и вероятность успеха одинакова при каждом проведении эксперимента.
Примером испытания Бернулли является подбрасывание монеты. Монета может приземлиться только с двух сторон (мы можем назвать орел «успехом», а решку «неудачей»), а вероятность успеха при каждом броске равна 0,5, если предположить, что монета честная.
Если случайная величина X подчиняется геометрическому распределению, то вероятность возникновения k отказов до первого успеха может быть найдена по следующей формуле:
P(X=k) = (1-p) k p
куда:
- k: количество неудач до первого успеха
- p: вероятность успеха в каждом испытании
В следующих примерах показано, как рассчитать вероятности, связанные с геометрическим распределением в Excel.
Пример 1: подбрасывание монеты
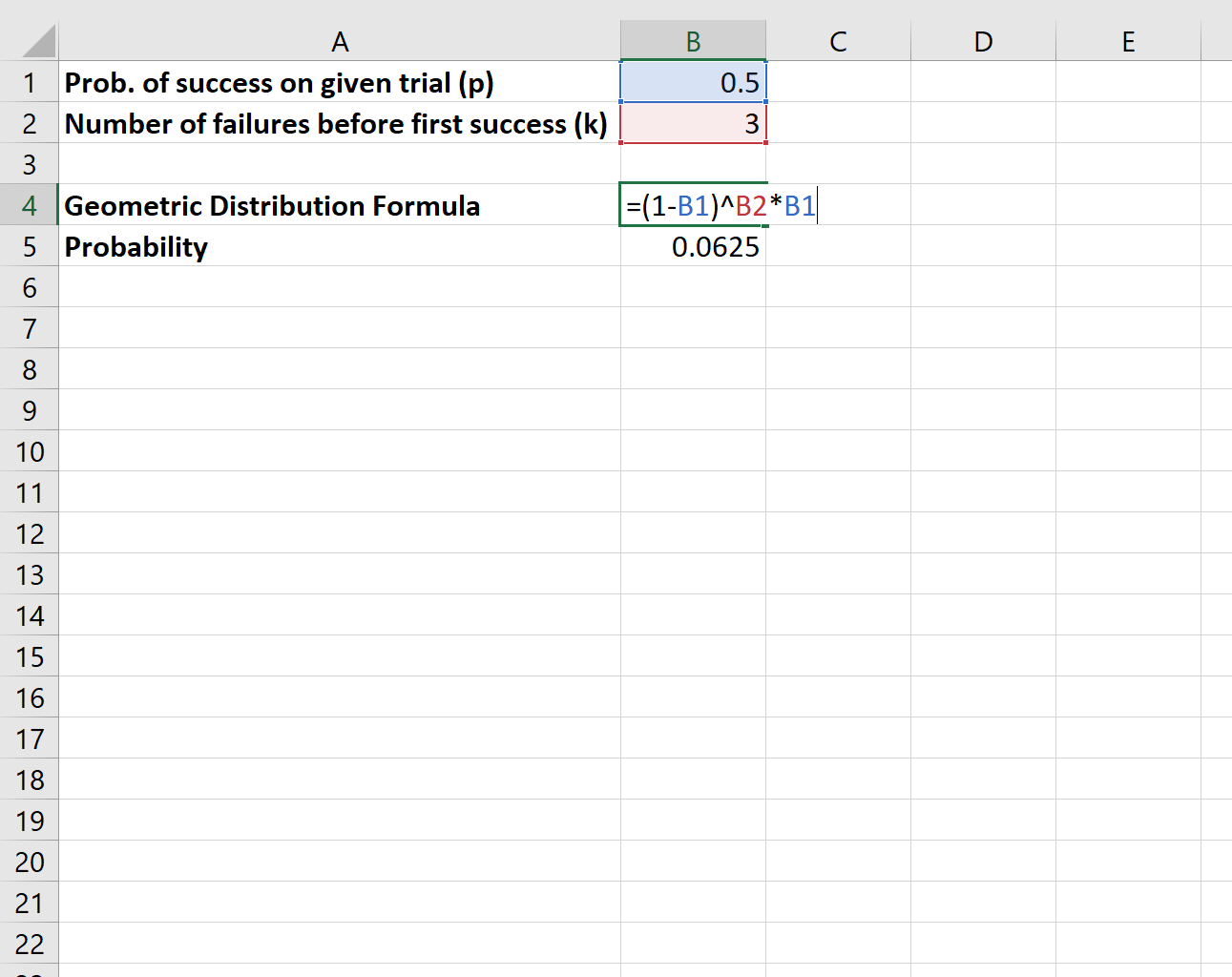
Предположим, мы подбрасываем монету и хотим узнать вероятность того, что потребуется ровно три «неудачи», прежде чем монета, наконец, упадет орлом.
Мы будем использовать следующую формулу для расчета этой вероятности:
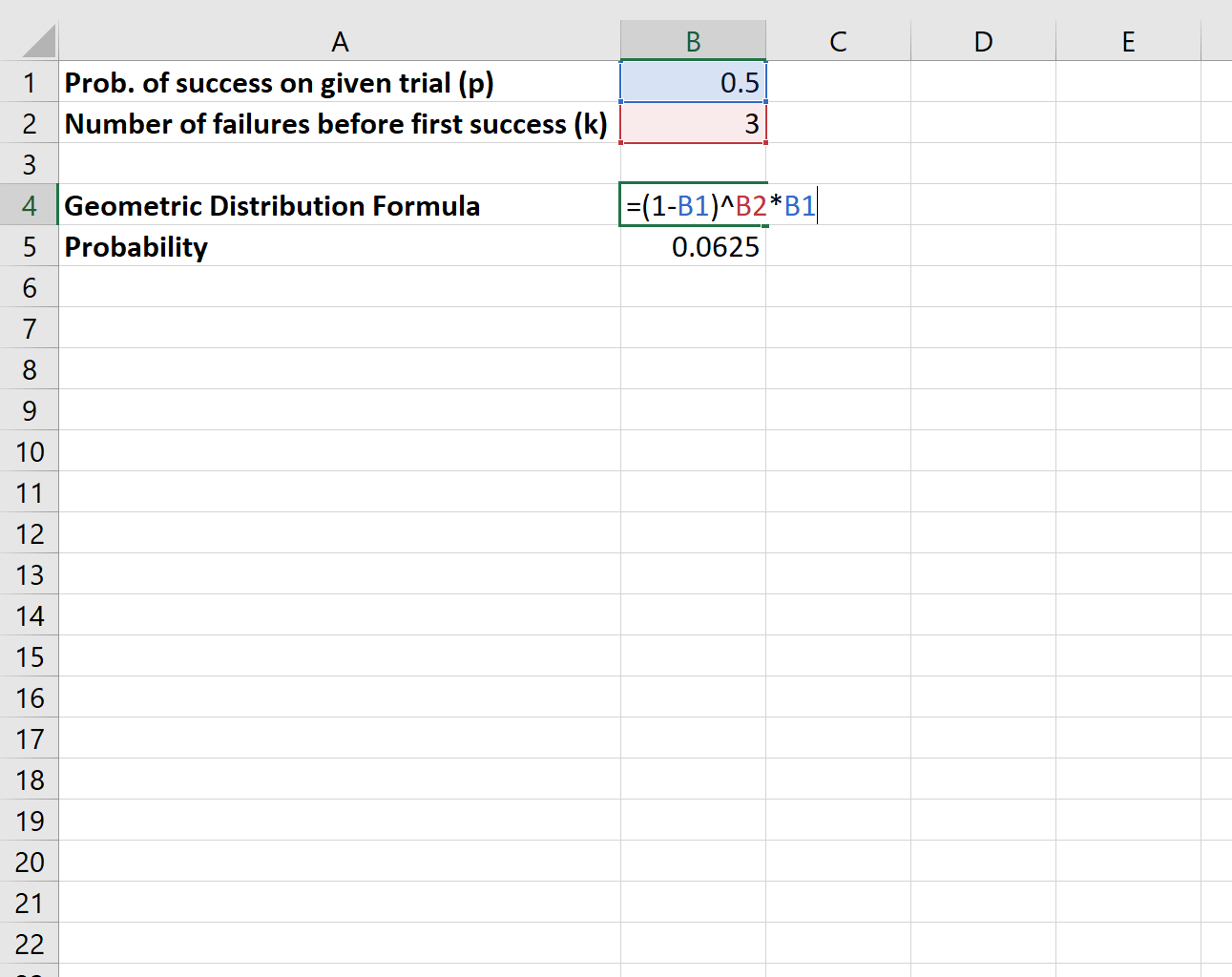
Вероятность того, что мы столкнемся с тремя «провалами», пока наконец монета не упадет орлом, равна 0,0625 .
Пример 2: штрафные броски
Предположим, некий баскетболист делает 60 % штрафных бросков. Какова вероятность того, что игрок пропустит четыре штрафных броска, пока, наконец, не сделает один?
Мы будем использовать следующую формулу для расчета этой вероятности:

Вероятность того, что игрок пропустит четыре штрафных броска, пока, наконец, не сделает один, равна 0,01536 .
Пример 3: Поддержка закона
Предположим, исследователь ждет за пределами библиотеки, чтобы спросить людей, поддерживают ли они определенный закон. Вероятность того, что данное лицо поддерживает закон, равна p = 0,2. Какова вероятность того, что четвертый человек, с которым разговаривает исследователь, первым поддержит закон?
Мы будем использовать следующую формулу для расчета этой вероятности:

Вероятность того, что четвертый человек, с которым разговаривает исследователь, первым поддержит закон, составляет 0,1024 .
Дополнительные ресурсы
Введение в геометрическое распределение
Калькулятор геометрического распределения
5 реальных примеров геометрического распределения