Тест на отсутствие соответствия используется для определения того, предлагает ли полная регрессионная модель значительно лучшее соответствие набору данных, чем некоторая сокращенная версия модели.
Например, предположим, что мы хотим использовать количество часов обучения , чтобы предсказать результаты экзаменов для студентов определенного колледжа. Мы можем решить использовать следующие две регрессионные модели:
Полная модель: оценка = β 0 + B 1 (часы) + B 2 (часы) 2
Сокращенная модель: оценка = β 0 + B 1 (часы)
В следующем пошаговом примере показано, как выполнить тест на отсутствие соответствия в R, чтобы определить, предлагает ли полная модель значительно лучшее соответствие, чем уменьшенная модель.
Шаг 1: Создайте и визуализируйте набор данных
Во-первых, мы будем использовать следующий код для создания набора данных, который содержит количество часов обучения и результаты экзаменов, полученные для 50 студентов:
#make this example reproducible
set. seed (1)
#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours\* runif (50, 1, 2)
#view first six rows of data
head(df)
hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510
Далее мы создадим диаграмму рассеяния, чтобы визуализировать взаимосвязь между количеством часов и счетом:
#load ggplot2 visualization package
library (ggplot2)
#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
geom_point()

Шаг 2. Подгонка двух разных моделей к набору данных
Далее мы подгоним к набору данных две разные модели регрессии:
#fit full model
full <- lm(score ~ poly (hours,2), data=df)
#fit reduced model
reduced <- lm(score ~ hours, data=df)
Шаг 3. Проведите тест на отсутствие пригодности
Далее мы воспользуемся командой anova() для проверки соответствия между двумя моделями:
#lack of fit test
anova(full, reduced)
Analysis of Variance Table
Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 368.48
2 48 451.22 -1 -82.744 10.554 0.002144 \*\*
---
Signif. codes: 0 ‘\*\*\*’ 0.001 ‘\*\*’ 0.01 ‘\*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Тестовая статистика F оказывается равной 10,554 , а соответствующее значение p равно 0,002144.Поскольку это p-значение меньше 0,05, мы можем отклонить нулевую гипотезу теста и сделать вывод, что полная модель предлагает статистически значимо лучшее соответствие, чем сокращенная модель.
Шаг 4: Визуализируйте окончательную модель
Наконец, мы можем визуализировать окончательную модель (полную модель) относительно исходного набора данных:
ggplot(df, aes (x=hours, y=score)) +
geom_point() +
stat_smooth(method='lm', formula = y ~ poly (x,2), size = 1) +
xlab('Hours Studied') +
ylab('Score')
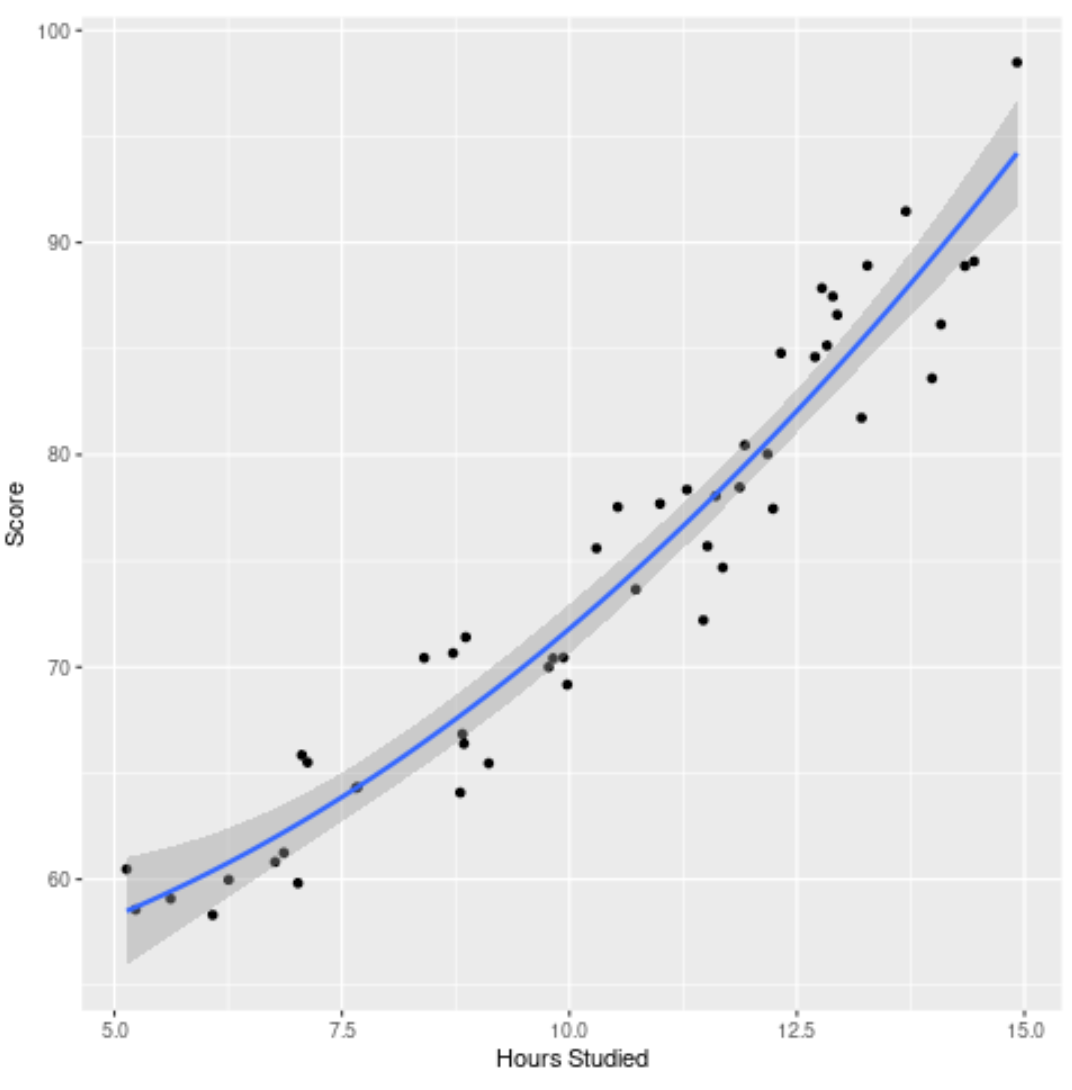
Мы видим, что кривая модели достаточно хорошо соответствует данным.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить полиномиальную регрессию в R