Линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между объясняющей переменной x и переменной отклика y.
В этом руководстве объясняется, как выполнить линейную регрессию на калькуляторе TI-84.
Пример: линейная регрессия на калькуляторе TI-84
Предположим, нас интересует взаимосвязь между количеством часов, которое студент тратит на подготовку к экзамену, и полученной им экзаменационной оценкой.
Чтобы изучить эту взаимосвязь, мы можем выполнить следующие шаги на калькуляторе TI-84, чтобы провести простую линейную регрессию, используя часы обучения в качестве независимой переменной и экзаменационный балл в качестве переменной ответа.
Шаг 1: Введите данные.
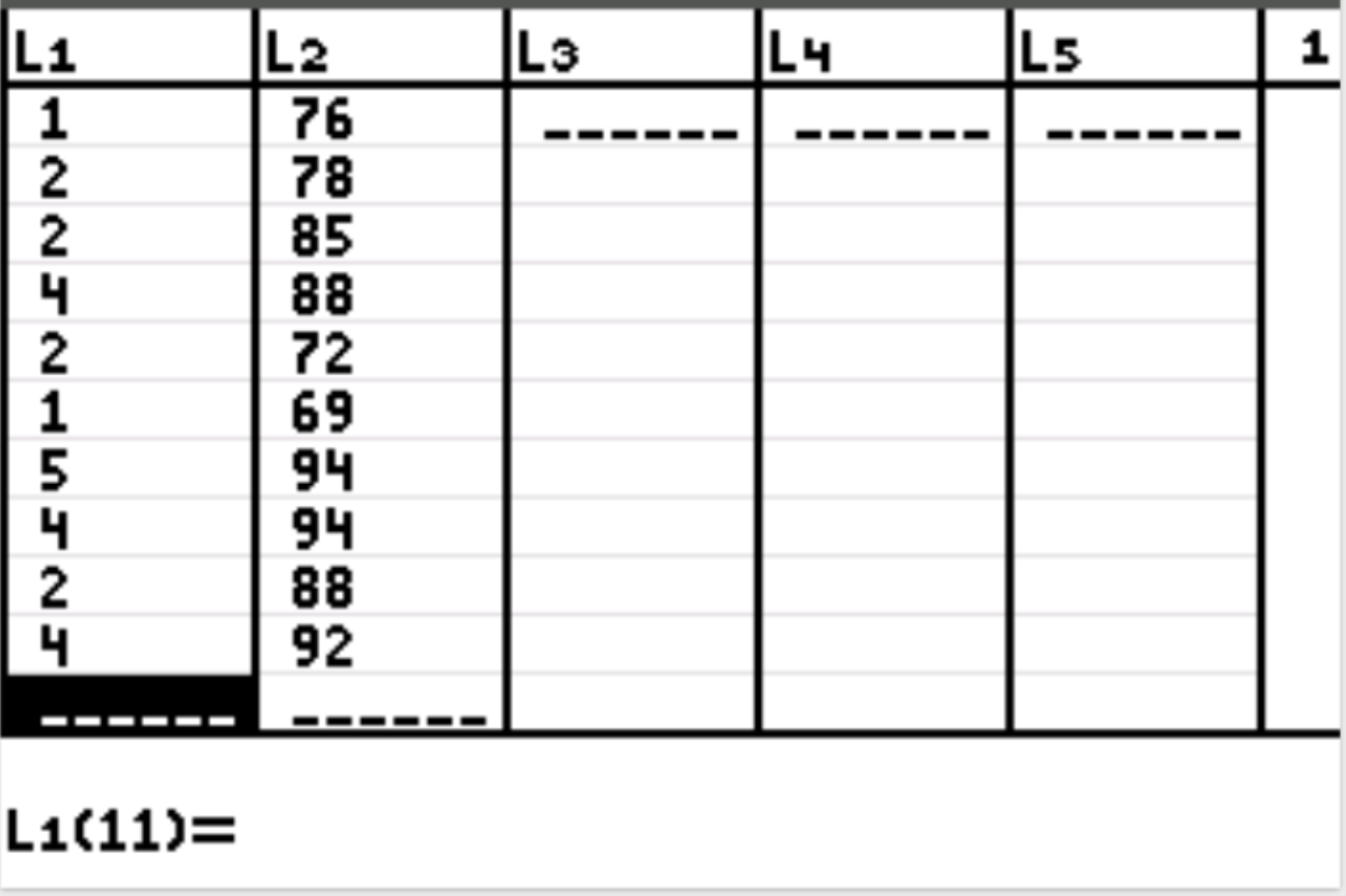
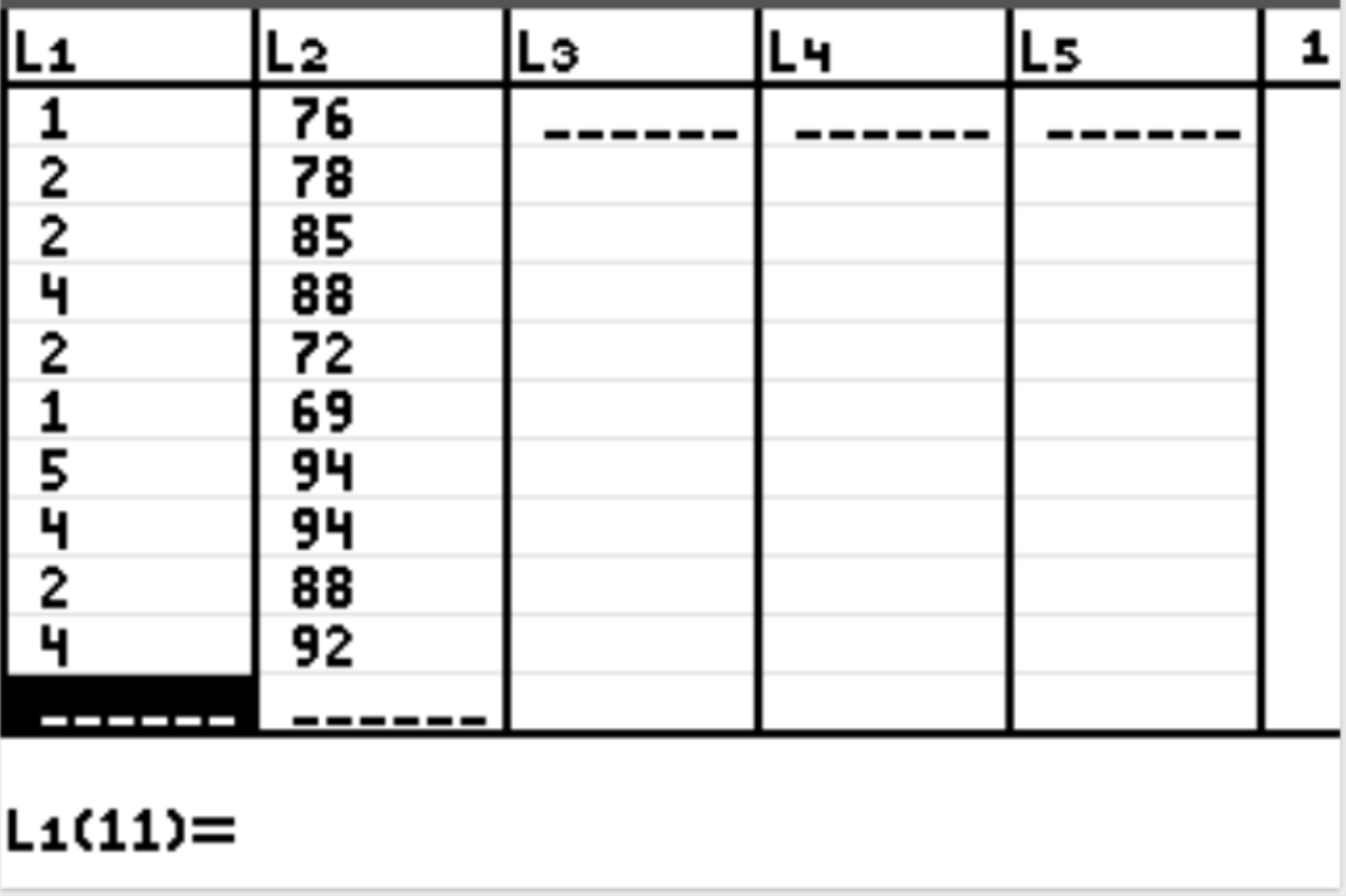
Сначала мы введем значения данных как для объясняющей, так и для ответной переменной. Нажмите Stat, а затем нажмите EDIT.Введите следующие значения для объясняющей переменной (часы обучения) в столбце L1 и значения для переменной ответа (экзаменационный балл) в столбце L2:
Шаг 2: Выполните линейную регрессию.
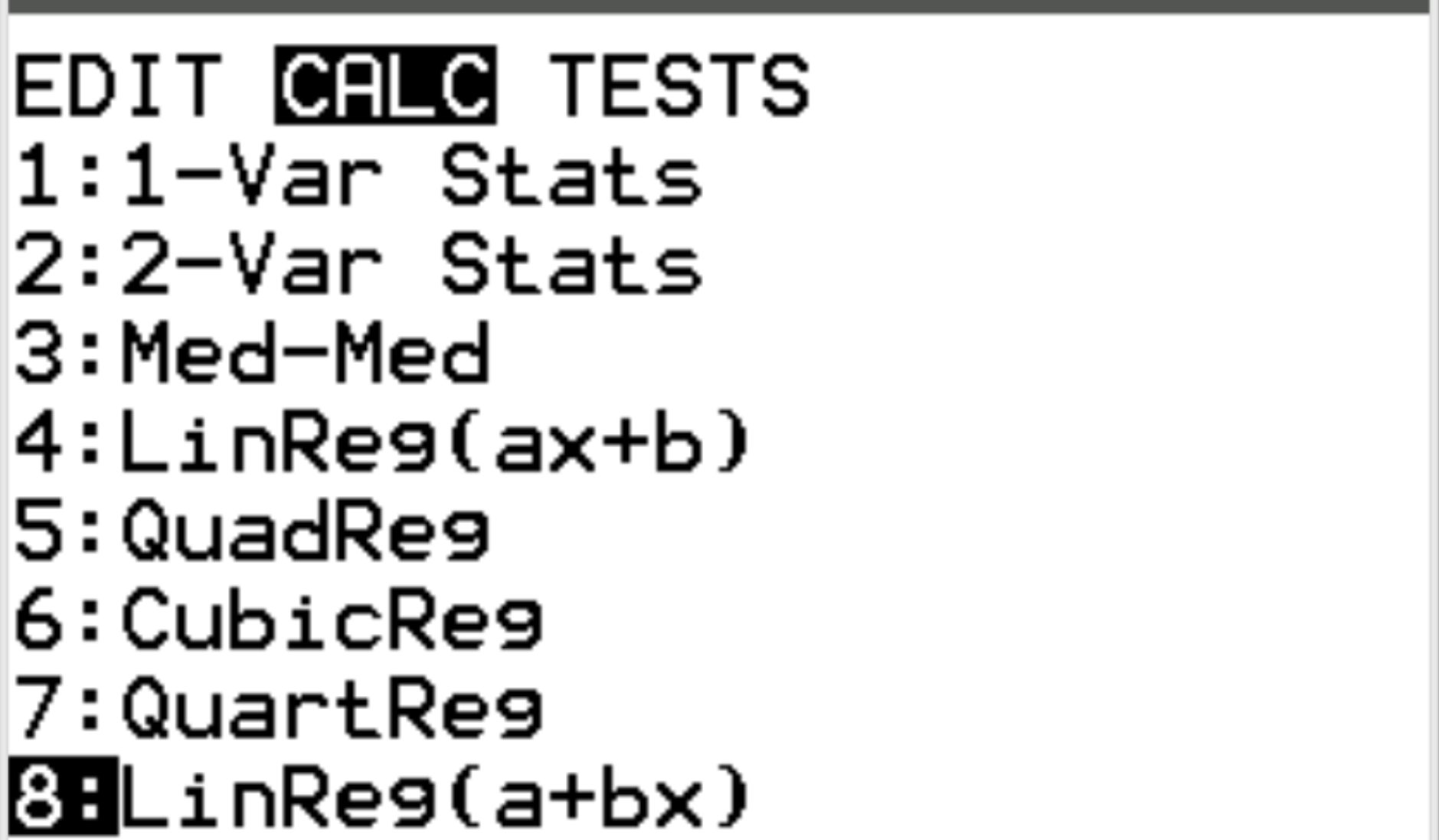
Далее мы выполним линейную регрессию. Нажмите Stat, а затем перейдите к CALC.Затем прокрутите вниз до 8: Linreg(a+bx) и нажмите Enter .
Для Xlist и Ylist убедитесь, что выбраны L1 и L2, так как это столбцы, которые мы использовали для ввода наших данных. Оставьте список частот пустым. Прокрутите вниз до пункта « Рассчитать » и нажмите «Ввод ». Автоматически появится следующий вывод:
Шаг 3: Интерпретируйте результаты.
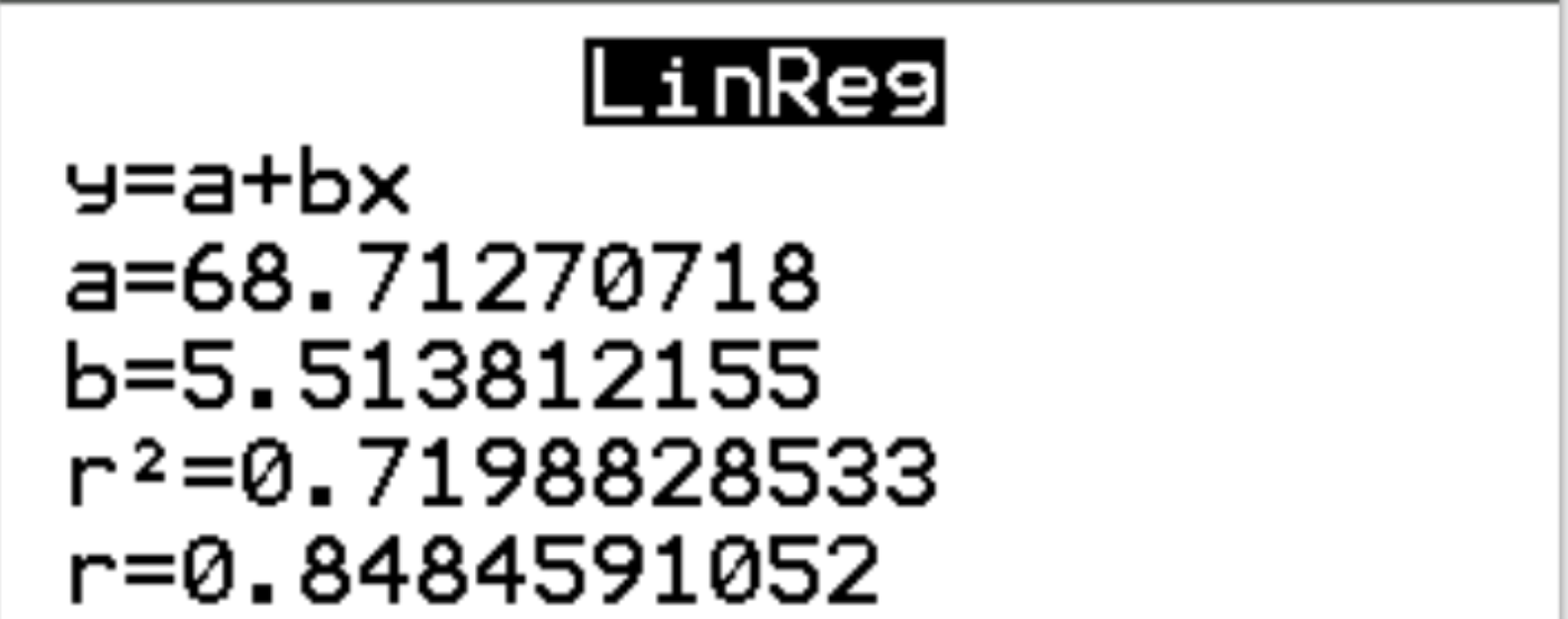
Из результатов мы видим, что оценочное уравнение регрессии выглядит следующим образом:
экзаменационный балл = 68,7127 + 5,5138*(часов)
Мы интерпретируем коэффициент для часов как означающий, что за каждый дополнительный час обучения ожидается увеличение экзаменационного балла в среднем на 5,5138.Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который изучает ноль часов, составляет 68,7127 .
Мы можем использовать это оценочное уравнение регрессии для расчета ожидаемого экзаменационного балла для учащегося на основе количества часов, которые он изучает.
Например, студент, который занимается три часа, должен получить экзаменационный балл 85,25 :
экзаменационный балл = 68,7127 + 5,5138*(3) = 85,25
Мы также можем видеть, что r-квадрат для регрессионной модели равен r 2 = 0,7199 .
Это значение известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющей переменной. В этом примере 71,99 % различий в баллах за экзамен можно объяснить количеством часов обучения.
Дополнительные ресурсы
Как построить график остатков на калькуляторе TI-84
Как выполнить квадратичную регрессию на калькуляторе TI-84
Как выполнить экспоненциальную регрессию на калькуляторе TI-84
Как выполнить логарифмическую регрессию на калькуляторе TI-84