Многие статистические тесты требуют, чтобы одна или несколько переменных были нормально распределены , чтобы результаты теста были надежными.
В этом руководстве объясняется несколько методов, которые вы можете использовать для проверки нормальности переменных в Stata.
Для каждого из этих методов мы будем использовать встроенный набор данных Stata с именем auto.Вы можете загрузить этот набор данных с помощью следующей команды:
сисус авто
Метод 1: гистограммы
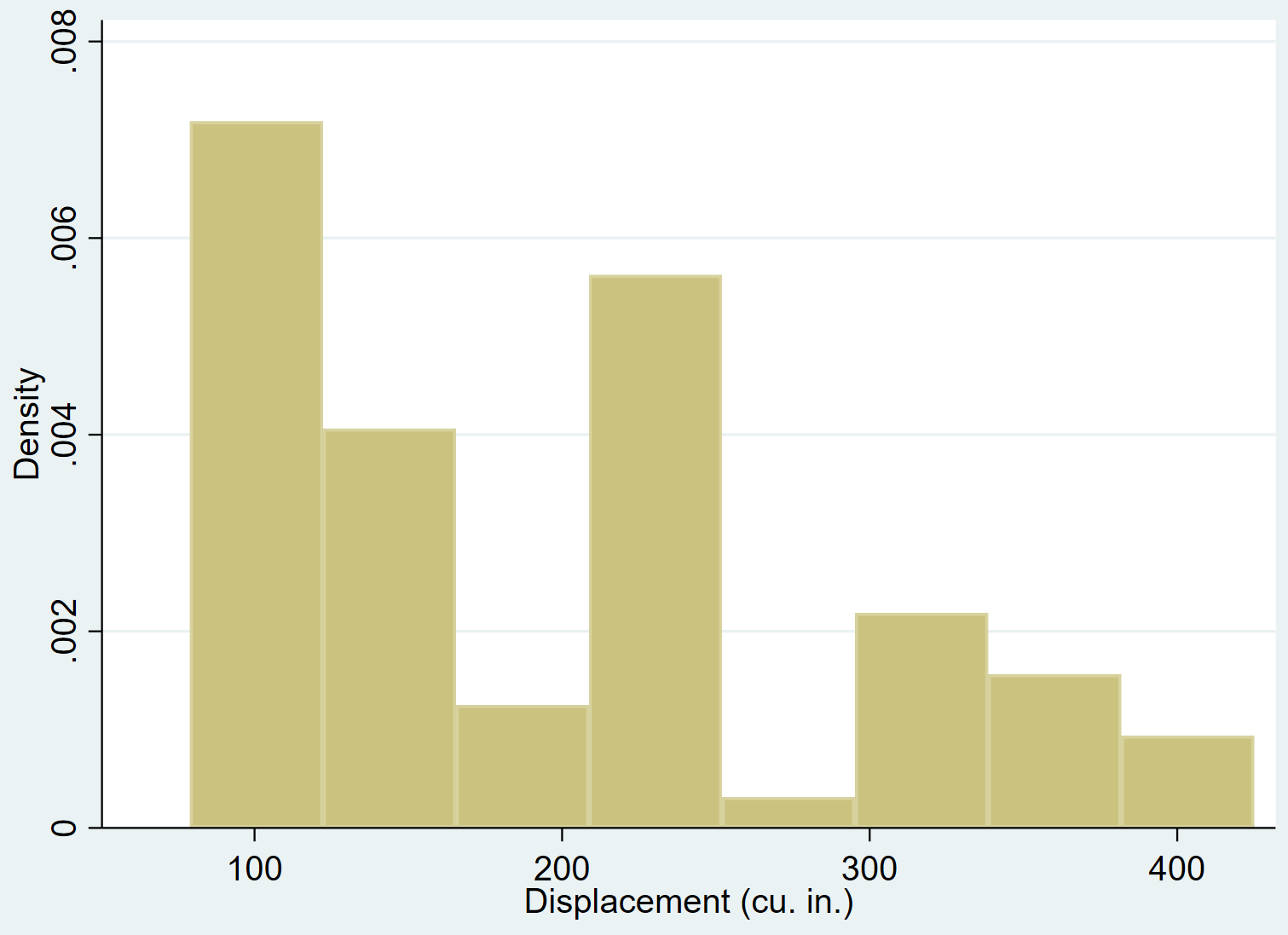
Один неформальный способ увидеть, нормально ли распределена переменная, — это создать гистограмму для просмотра распределения переменной.
Если переменная распределена нормально, гистограмма должна принять форму «колокола» с большим количеством значений, расположенных ближе к центру, и меньшим количеством значений, расположенных на хвостах.
Мы можем использовать команду hist для создания гистограммы для переменного смещения :
его смещение
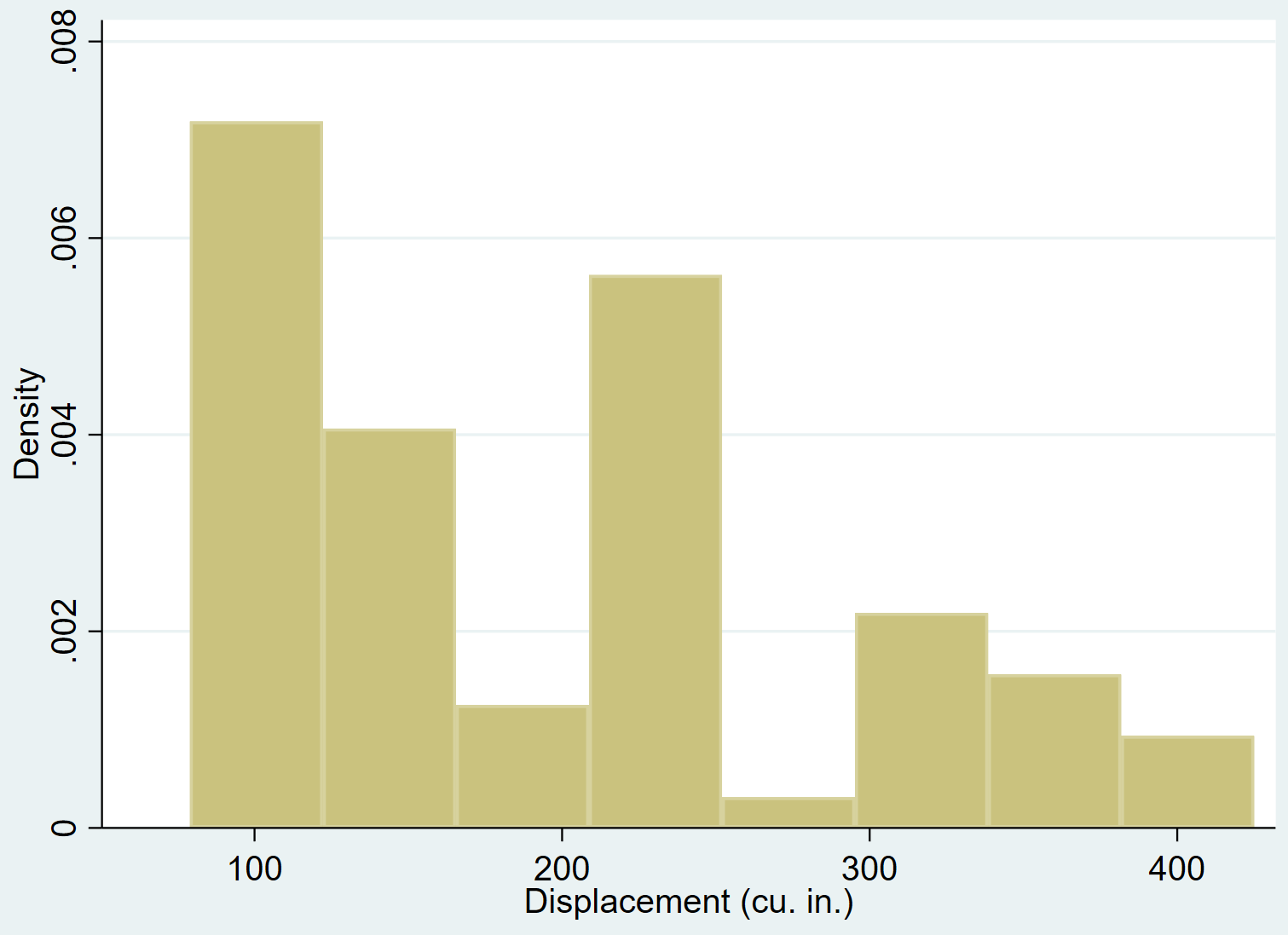
Мы можем добавить кривую нормальной плотности к гистограмме с помощью команды normal :
смещение, нормальное
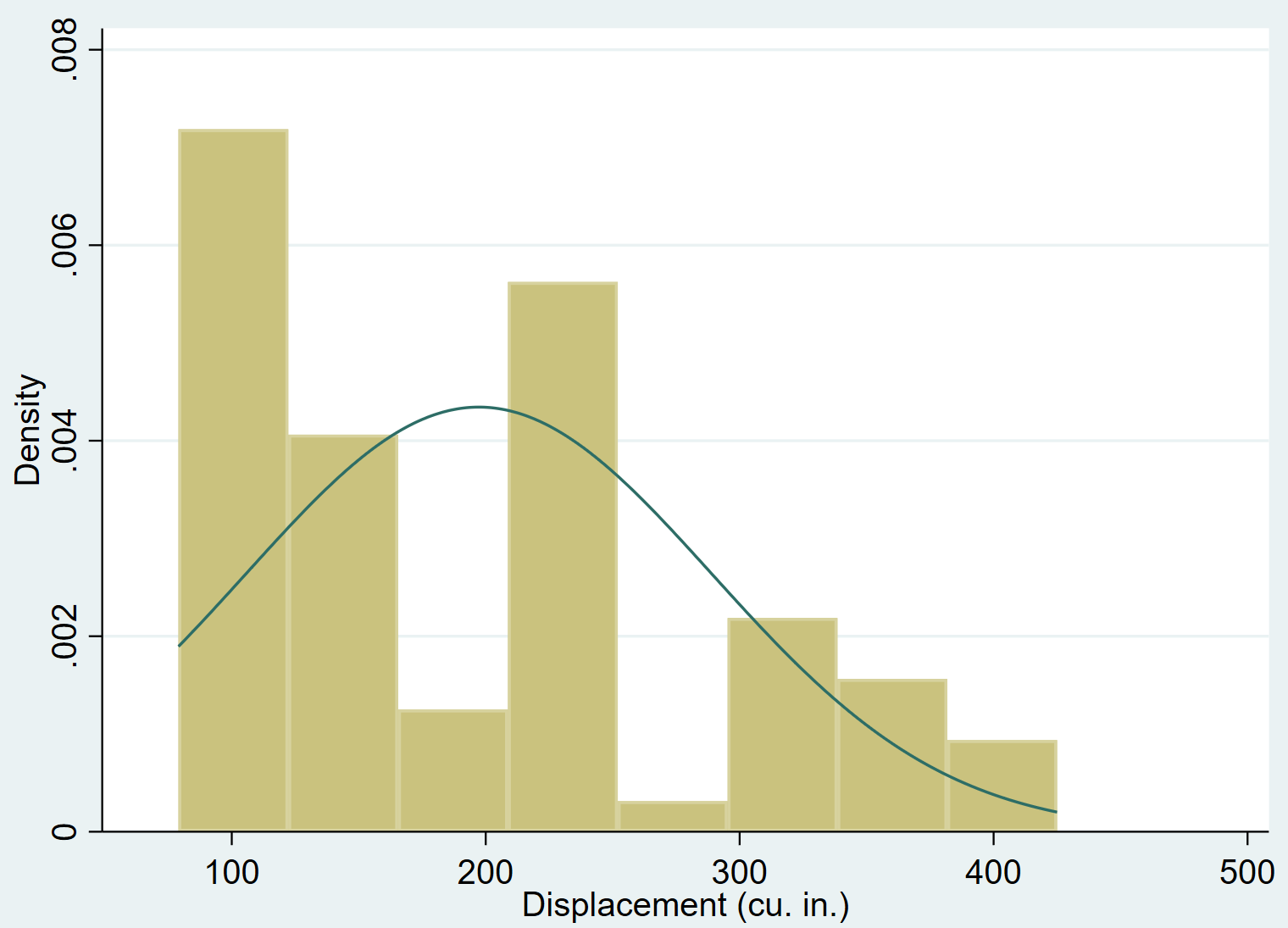
Совершенно очевидно, что смещение переменной смещено вправо (например, большинство значений сконцентрировано слева, а длинный «хвост» значений простирается вправо) и не подчиняется нормальному распределению.
Связанный: Левостороннее и правостороннее распределение
Метод 2: Тест Шапиро-Уилка
Формальный способ проверить нормальность — использовать тест Шапиро-Уилка .
Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если p-значение теста меньше некоторого уровня значимости (обычный выбор включает 0,01, 0,05 и 0,10), то мы можем отклонить нулевую гипотезу и сделать вывод, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.
*Этот тест можно использовать, когда общее количество наблюдений составляет от 4 до 2000.
Мы можем использовать команду swilk для выполнения теста Шапиро-Уилка для переменного смещения :
водоизмещение

Вот как интерпретировать вывод теста:
Obs: 74. Это количество наблюдений, использованных в тесте.
Вт: 0,92542. Это тестовая статистика для теста.
Вероятность z: 0,00031. Это p-значение, связанное со статистикой теста.
Поскольку p-значение меньше 0,05, мы можем отклонить нулевую гипотезу теста. У нас есть достаточно доказательств, чтобы сказать, что переменное смещение не имеет нормального распределения.
Мы также можем выполнить тест Шапиро-Уилка для более чем одной переменной одновременно, указав несколько переменных после команды swilk :
объем двигателя swilk длина миль на галлон
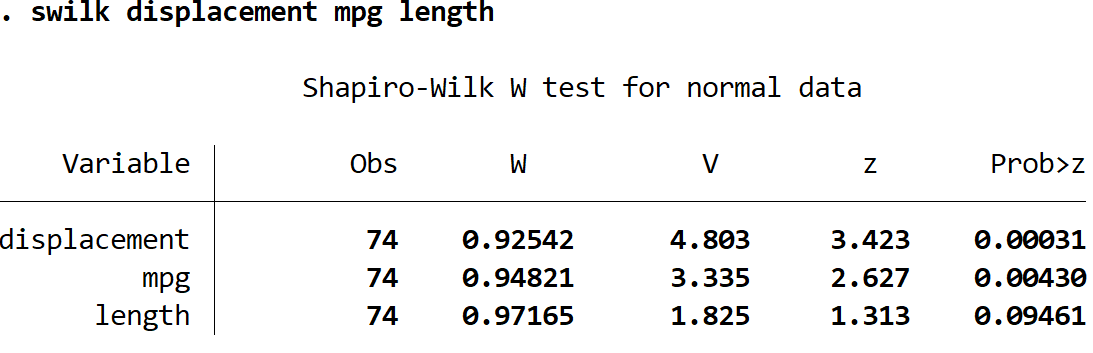
Используя уровень значимости 0,05, мы пришли бы к выводу, что смещение и мили на галлон распределены ненормально, но у нас нет достаточных доказательств, чтобы сказать, что длина распределена ненормально.
Метод 3: Тест Шапиро-Франсиа
Другой формальный способ проверить нормальность — использовать тест Шапиро-Франсиа .
Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если p-значение теста меньше некоторого уровня значимости, то мы можем отклонить нулевую гипотезу и сделать вывод, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.
*Этот тест можно использовать, когда общее количество наблюдений составляет от 10 до 5000.
Мы можем использовать команду sfrancia для выполнения теста Шапиро-Уилка для переменного смещения :
смещение

Вот как интерпретировать вывод теста:
Obs: 74. Это количество наблюдений, использованных в тесте.
W': 0,93011. Это тестовая статистика для теста.
Вероятность z: 0,00094. Это p-значение, связанное со статистикой теста.
Поскольку p-значение меньше 0,05, мы можем отклонить нулевую гипотезу теста. У нас есть достаточно доказательств, чтобы сказать, что переменное смещение не имеет нормального распределения.
Подобно тесту Шапиро-Уилка, вы можете выполнить тест Шапиро-Франсиа одновременно для нескольких переменных, указав несколько переменных после команды sfrancia .
Метод 4: Тест на асимметрию и эксцесс
Другой способ проверить нормальность — использовать тест асимметрии и эксцесса, который определяет, согласуется ли асимметрия и эксцесс переменной с нормальным распределением.
Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если p-значение теста меньше некоторого уровня значимости, то мы можем отклонить нулевую гипотезу и сделать вывод, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.
*Для этого теста требуется минимум 8 наблюдений.
Мы можем использовать команду sktest для выполнения теста на асимметрию и эксцесс для переменного смещения :
смещение

Вот как интерпретировать вывод теста:
Obs: 74. Это количество наблюдений, использованных в тесте.
прил чи (2): 5,81. Это статистика теста хи-квадрат для теста.
Prop>chi2: 0,0547. Это p-значение, связанное со статистикой теста.
Поскольку значение p не менее 0,05, мы не можем отвергнуть нулевую гипотезу теста. У нас нет достаточных доказательств, чтобы сказать, что смещение не распределяется нормально.
Подобно другим тестам на нормальность, вы можете выполнить тест на асимметрию и эксцесс одновременно с несколькими переменными, указав несколько переменных после команды sktest .