Частичный F-тест используется для определения того, существует ли статистически значимое различие между регрессионной моделью и некоторой вложенной версией той же модели.
Вложенная модель — это просто модель, которая содержит подмножество переменных-предикторов в общей регрессионной модели.
Например, предположим, что у нас есть следующая регрессионная модель с четырьмя переменными-предикторами:
Y = β 0 + β 1 х 1 + β 2 х 2 + β 3 х 3 + β 4 х 4 + ε
Одним из примеров вложенной модели может быть следующая модель только с двумя исходными предикторными переменными:
Y = β 0 + β 1 х 1 + β 2 х 2 + ε
Чтобы определить, существенно ли различаются эти две модели, мы можем выполнить частичный F-тест, который вычисляет следующую статистику F-теста:
F = (( сокращенный RSS – полный RSS)/p) / ( полный RSS/nk)
куда:
- Сокращенный RSS : Остаточная сумма квадратов сокращенной (т.е. «вложенной») модели.
- RSS full : остаточная сумма квадратов полной модели.
- p: количество предикторов, удаленных из полной модели.
- n: общее количество наблюдений в наборе данных.
- k: количество коэффициентов (включая точку пересечения) в полной модели.
В этом тесте используются следующие нулевая и альтернативная гипотезы :
H 0 : Все коэффициенты, удаленные из полной модели, равны нулю.
H A : По крайней мере один из коэффициентов, удаленных из полной модели, отличен от нуля.
Если значение p, соответствующее статистике F-теста, ниже определенного уровня значимости (например, 0,05), то мы можем отклонить нулевую гипотезу и сделать вывод, что по крайней мере один из коэффициентов, удаленных из полной модели, является значимым.
В следующем примере показано, как выполнить частичный F-тест в Excel.
Пример: Частичный F-тест в Excel
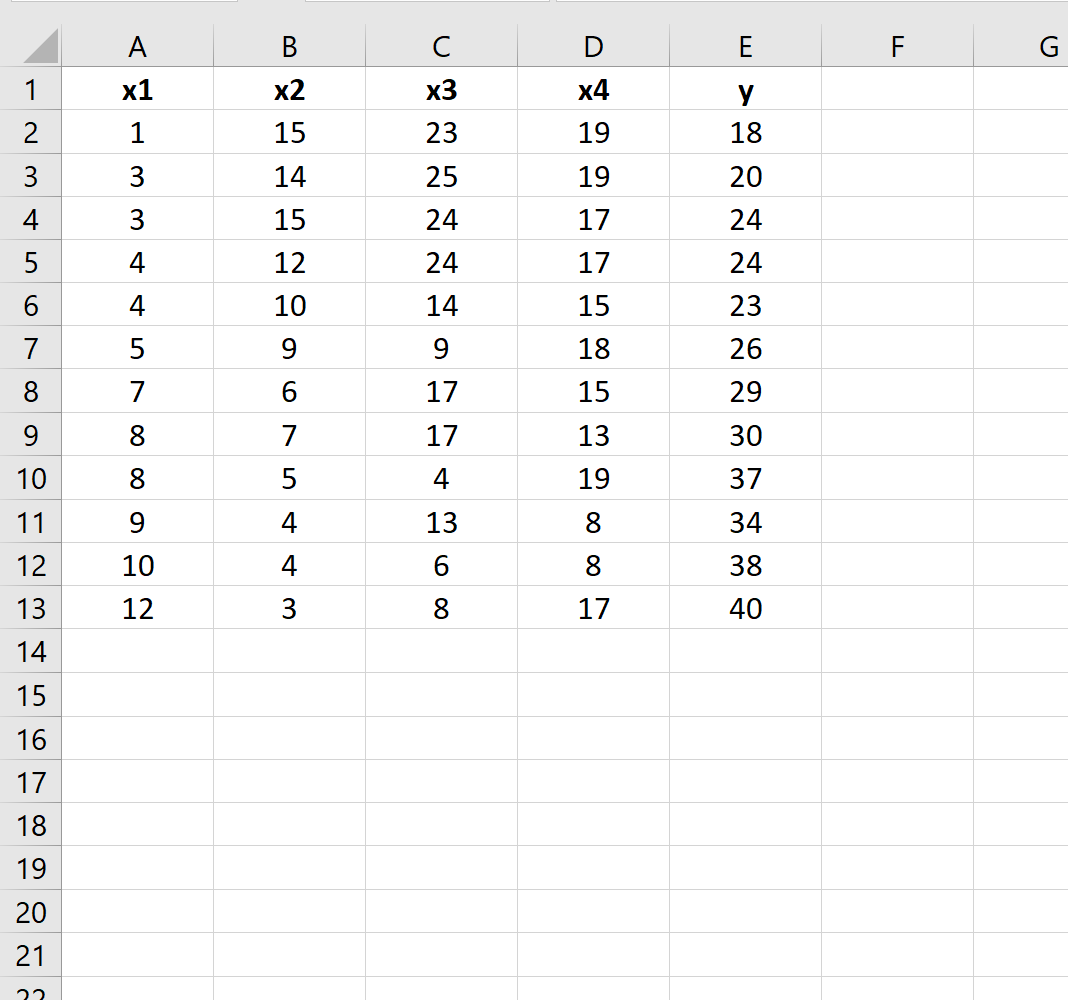
Предположим, у нас есть следующий набор данных в Excel:

Предположим, мы хотели бы определить, есть ли разница между следующими двумя регрессионными моделями:
Полная модель: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
Уменьшенная модель: y = β 0 + β 1 x 1 + β 2 x 2
Мы можем приступить к выполнению множественной линейной регрессии в Excel для каждой модели, чтобы получить следующий результат:

Затем мы можем использовать следующую формулу для расчета статистики F-теста для частичного F-теста:

Тестовая статистика оказывается 2,064 .
Затем мы можем использовать следующую формулу для вычисления соответствующего p-значения:

Значение p оказывается равным 0,1974 .
Поскольку это p-значение не меньше 0,05, мы не сможем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы сказать, что любая из переменных-предикторов x3 или x4 является статистически значимой.
Другими словами, добавление x3 и x4 к регрессионной модели существенно не улучшает соответствие модели.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как рассчитать стандартную ошибку регрессии в Excel