Коэффициент частичной регрессии — это имя, данное коэффициентам регрессии в модели множественной линейной регрессии .
Это отличается от старого доброго «коэффициента регрессии», которым называют коэффициент регрессии в простой модели линейной регрессии .
Способ интерпретации коэффициента частичной регрессии: среднее изменение переменной отклика , связанное с увеличением на одну единицу данной переменной-предиктора, при условии, что все другие переменные-предикторы остаются постоянными.
В следующем примере объясняется, как идентифицировать и интерпретировать коэффициенты частичной регрессии в модели множественной линейной регрессии.
Пример: интерпретация коэффициентов частичной регрессии
Предположим, мы хотим знать, влияет ли количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов на балл, который студент получает на определенном вступительном экзамене в колледж.
Чтобы исследовать эту взаимосвязь, мы можем подобрать модель множественной линейной регрессии, используя часы обучения и подготовительные экзамены, взятые в качестве переменных-предикторов, и экзаменационный балл в качестве переменной ответа.
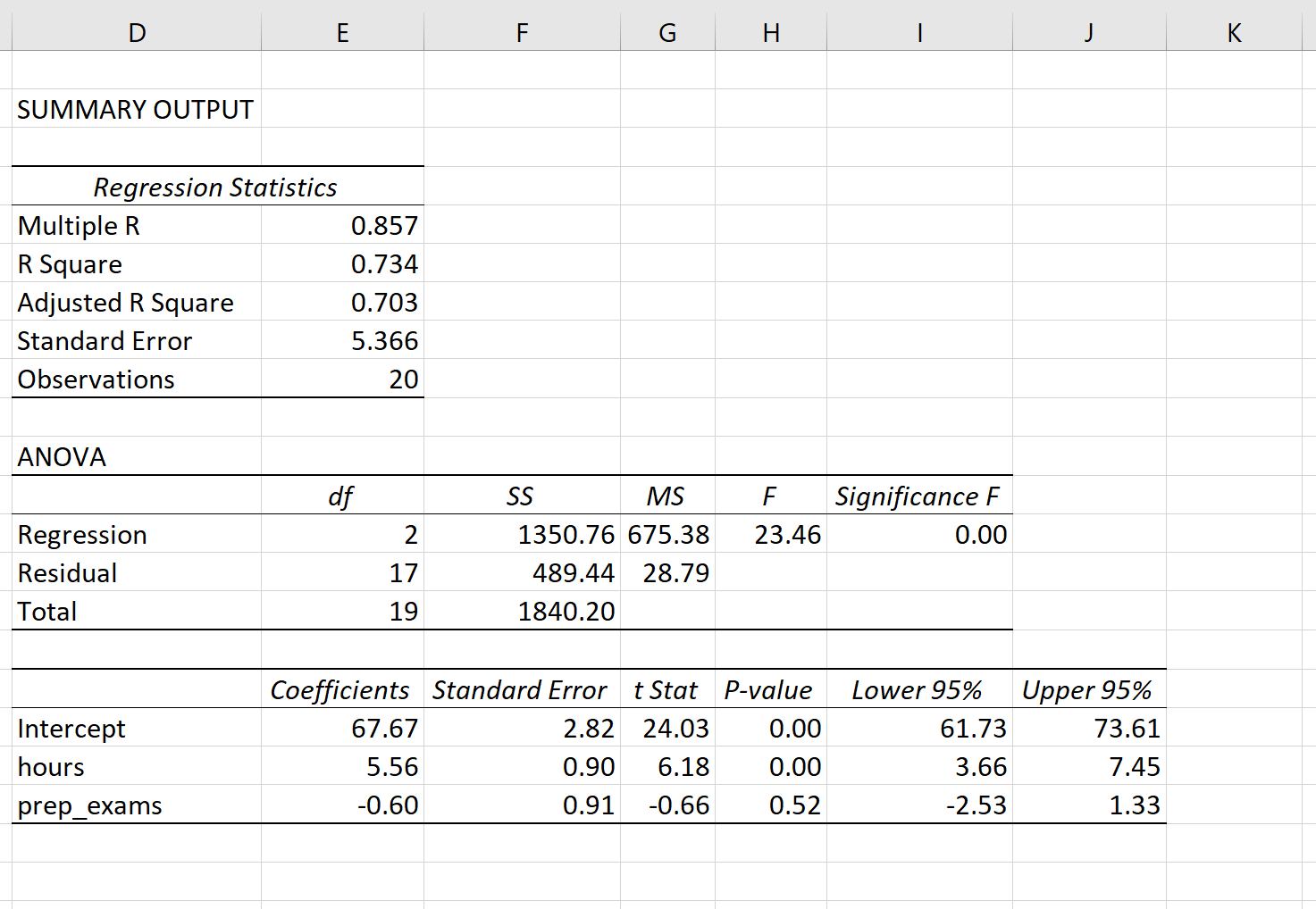
В следующей таблице регрессии показаны выходные данные модели:
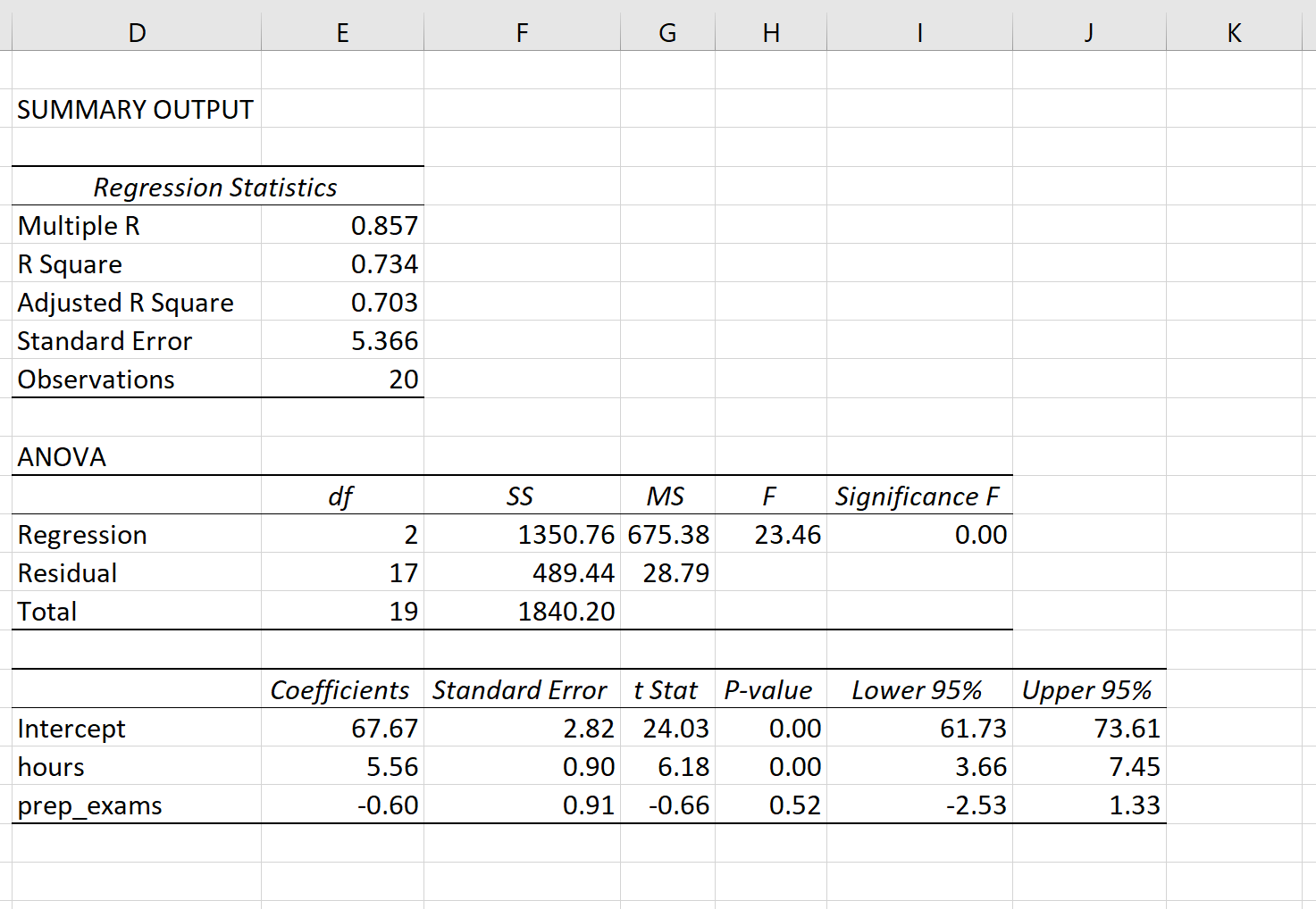
Вот как интерпретировать коэффициенты частичной регрессии:
Часы: за каждый дополнительный час, потраченный на обучение, экзаменационная оценка увеличивается в среднем на 5,56 балла, при условии, что количество подготовительных экзаменов остается постоянным.
Вот еще один способ подумать об этом: если учащийся A и учащийся B сдают одинаковое количество подготовительных экзаменов, но учащийся A учится на один час больше, то ожидается, что учащийся A наберет на 5,56 балла больше, чем учащийся B.
Подготовительные экзамены: за каждый дополнительный подготовительный экзамен экзаменационная оценка уменьшается в среднем на 0,60 балла, при условии, что количество часов обучения остается постоянным.
Другой способ подумать об этом: если учащийся А и учащийся Б учатся одинаковое количество часов, но учащийся А сдает один дополнительный подготовительный экзамен, то ожидается, что учащийся А получит оценку на 0,60 балла ниже, чем учащийся Б.
Используя коэффициенты из выходных данных регрессии, мы можем написать оценочное уравнение множественной линейной регрессии:
Экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Мы можем использовать это оценочное уравнение регрессии, чтобы рассчитать ожидаемый балл экзамена для учащегося на основе количества часов, которые он изучает, и количества подготовительных экзаменов, которые он сдает.
Например, студент, который занимается три часа и сдает один подготовительный экзамен, должен получить 83,75 балла:
Экзаменационный балл = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Дополнительные ресурсы
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Как читать и интерпретировать таблицу регрессии