Множественная линейная регрессия — это статистический метод, который мы можем использовать для понимания взаимосвязи между несколькими переменными-предикторами и переменной- откликом .
Однако одно из ключевых предположений множественной линейной регрессии заключается в том, что существует линейная связь между каждой переменной-предиктором и переменной-ответом.
Если это допущение нарушается, то результаты регрессионной модели могут быть недостоверными.
Один из способов проверить это предположение — создать график частичных остатков , на котором отображаются остатки одной переменной-предиктора по сравнению с переменной-откликом.
В следующем примере показано, как создать частичные остаточные графики для регрессионной модели в R.
Пример: как создать графики частичных остатков в R
Предположим, мы подогнали регрессионную модель с тремя переменными-предикторами в R:
#make this example reproducible
set. seed (0)
#define response variable
y <- c(1:1000)
#define three predictor variables
x1 <- c(1:1000)\*runif(n=1000)
x2 <- (c(1:1000)\*rnorm(n=1000))^2
x3 <- (c(1:1000)\*rnorm(n=1000))^3
#fit multiple linear regression model
model <- lm(y~x1+x2+x3))
Мы можем использовать функцию crPlots() из пакета car в R, чтобы создать частичные остаточные графики для каждой переменной-предиктора в модели:
library (car)
#create partial residual plots
crPlots(model)
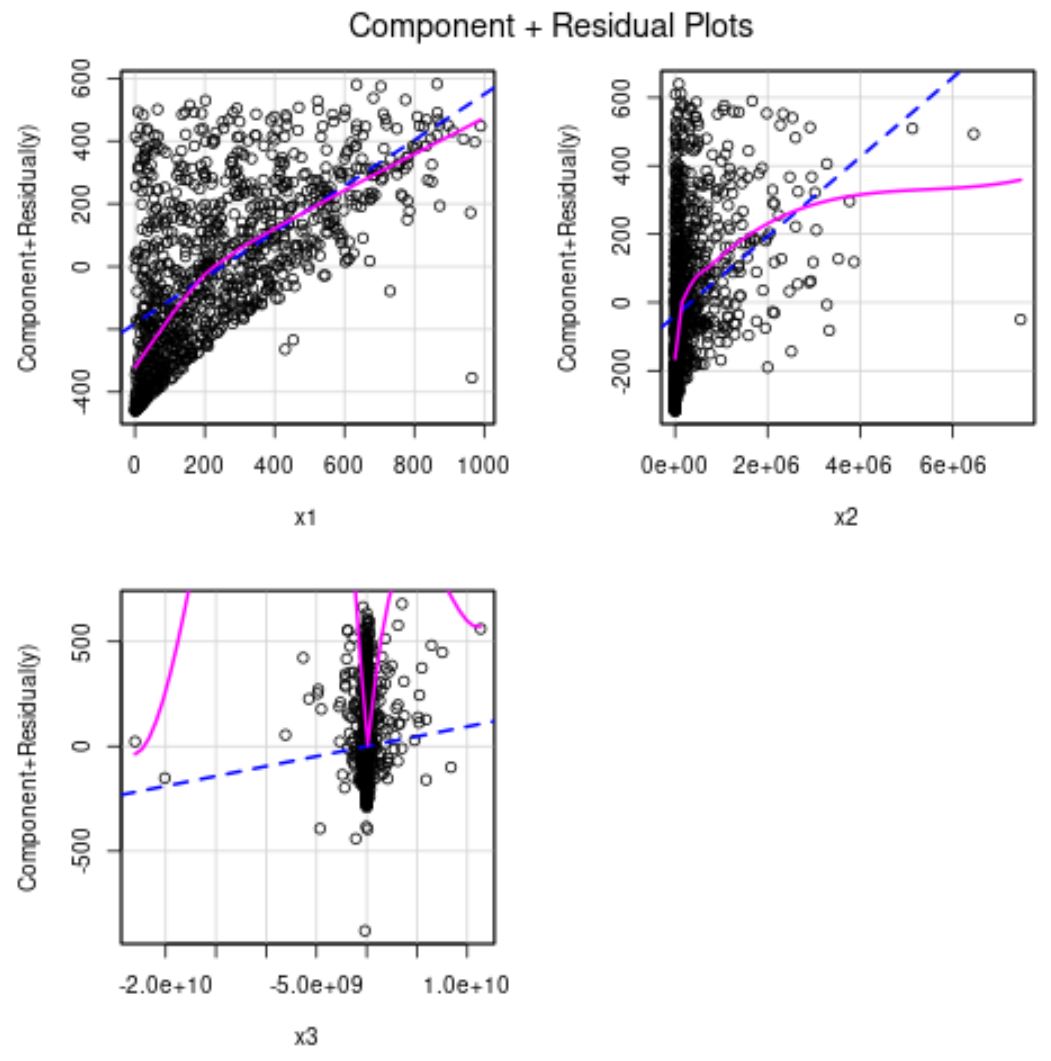
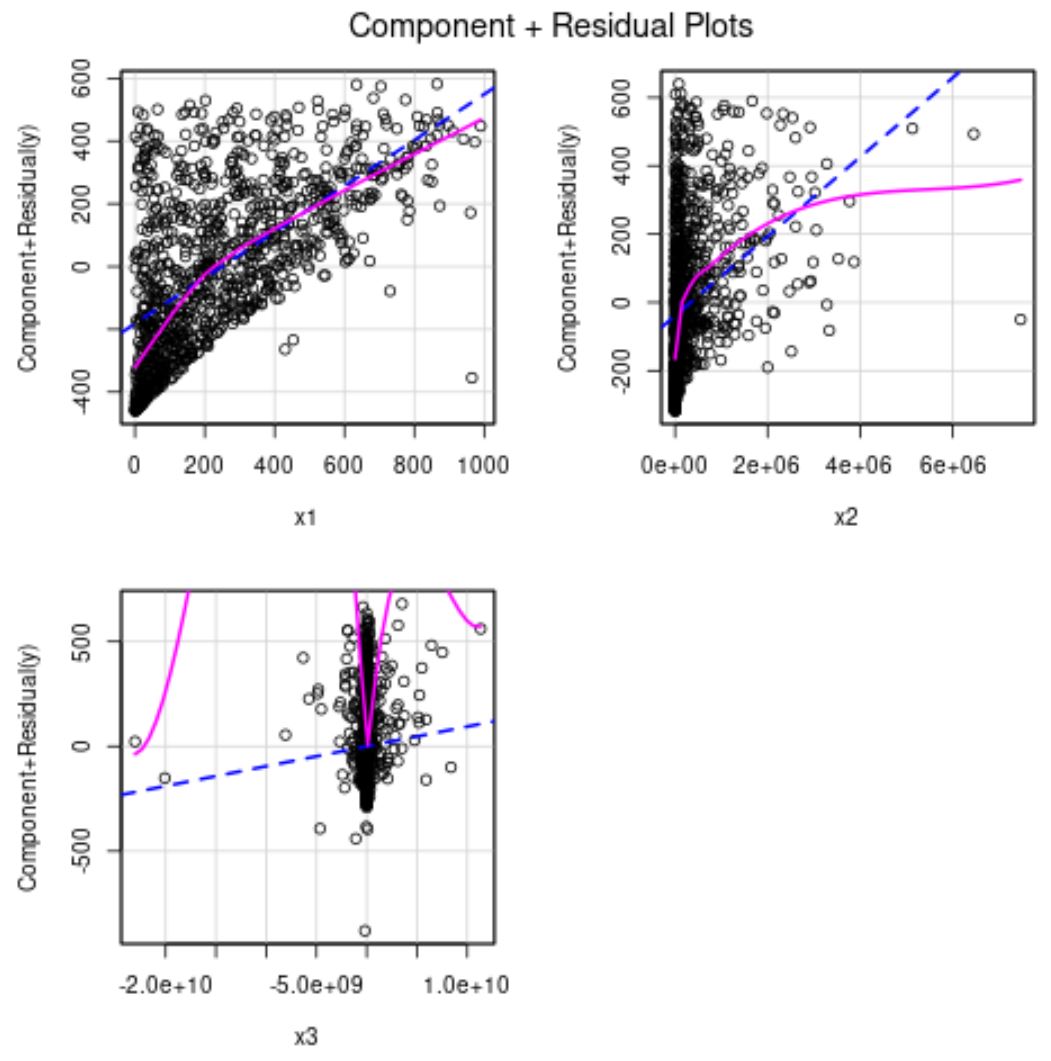
Синяя линия показывает ожидаемые остатки, если связь между предиктором и переменной отклика была линейной. Розовая линия показывает фактические остатки.
Если две линии существенно отличаются, то это свидетельствует о нелинейной зависимости.
Из приведенных выше графиков видно, что остатки как для x2, так и для x3 кажутся нелинейными.
Это нарушает предположение о линейности множественной линейной регрессии. Один из способов решить эту проблему — использовать квадратный корень или кубическое преобразование переменных-предикторов:
library (car)
#fit new model with transformed predictor variables
model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3)))
#create partial residual plots for new model
crPlots(model_transformed)

Из графиков частичных остатков мы видим, что x2 теперь имеет более линейную связь с переменной отклика.
Предикторная переменная x3 все еще несколько нелинейна, поэтому мы можем решить попробовать другое преобразование или, возможно, вообще исключить переменную из модели.
Дополнительные ресурсы
В следующих руководствах объясняется, как создавать другие распространенные графики в R:
Как создавать диагностические графики в R
Как создать график масштабирования-местоположения в R
Как создать остаточный график в R