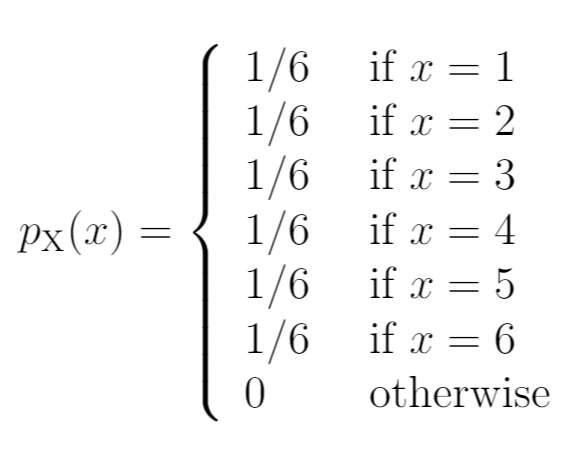Функция массы вероятности , часто сокращенно PMF , говорит нам о вероятности того, что дискретная случайная величина примет определенное значение.
Например, предположим, что мы бросаем кости один раз. Если мы позволим x обозначать число, на которое выпадет игральная кость, то вероятность того, что x будет равна разным значениям, можно описать следующим образом:
- Р(Х=1): 1/6
- Р(Х=2): 1/6
- Р(Х=3): 1/6
- Р(Х=4): 1/6
- Р(Х=5): 1/6
- Р(Х=6): 1/6
Существует равная вероятность того, что кости могут выпасть на любое число от 1 до 6.
Вот как мы запишем эти вероятности в виде функции массы вероятности:
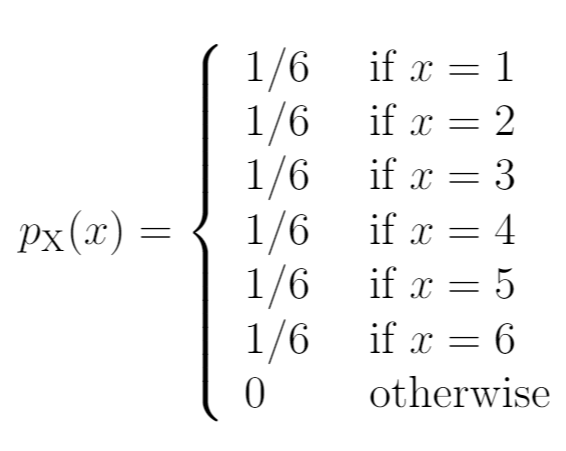
В левой части диаграммы показана вероятность, связанная с исходами в правой части:

Одной из характеристик функции массы вероятности является то, что все вероятности должны в сумме давать 1. Вы заметите, что эта PMF удовлетворяет этому условию:
Сумма вероятностей = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.
Поддержка функции массы вероятности относится к набору значений, которые может принимать дискретная случайная величина. В этом примере поддержкой будет {1, 2, 3, 4, 5, 6}, поскольку значение костей может принимать любое из этих значений.
Вне опоры значение PMF равно нулю. Например, вероятность того, что кубик выпадет на «0», «7» или «8», равна нулю, поскольку ни одно из этих чисел не включено в опору.
Функции массы вероятности на практике
Двумя наиболее распространенными примерами функций массы вероятности на практике являются биномиальное распределение и распределение Пуассона .
Биномиальное распределение
Если случайная величина X следует биномиальному распределению, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = n C k * p k * (1-p) nk
куда:
- n: количество испытаний
- k: количество успехов
- p: вероятность успеха в данном испытании
- n C k : количество способов добиться k успехов в n испытаниях.
Например, предположим, что мы подбрасываем монету 3 раза. Мы можем использовать приведенную выше формулу, чтобы определить вероятность получения 0, 1, 2 и 3 решек во время этих 3 подбрасываний:
- P(X=0) = 3 C 0 * 0,5 0 * (1-0,5) 3-0 = 1 * 1 * (0,5) 3 = 0,125
- P(X=1) = 3 C 1 * 0,5 1 * (1-0,5) 3-1 = 1 * 1 * (0,5) 2 = 0,375
- P(X=2) = 3 C 2 * 0,5 2 * (1-0,5) 3-2 = 1 * 1 * (0,5) 1 = 0,375
- P(X=3) = 3 C 3 * 0,5 3 * (1-0,5) 3-3 = 1 * 1 * (0,5) 0 = 0,125
Распределение Пуассона
Если случайная величина X подчиняется распределению Пуассона, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = λk * e – λ / k !
куда:
- λ: среднее количество успехов за определенный интервал
- k: количество успехов
- e: константа, равная приблизительно 2,71828.
Например, предположим, что в конкретной больнице в среднем рождается 2 человека в час. Мы можем использовать приведенную выше формулу, чтобы определить вероятность рождения 0, 1, 2, 3 и т. д. в данный час:
- P(X=0) = 2 0 * e – 2 / 0! = 0,1353
- P(X=1) = 2 1 * e – 2 / 1! = 0,2707
- P(X=2) = 2 2 * e – 2 / 2! = 0,2707
- P(X=3) = 2 3 * e – 2 / 3! = 0,1805
Визуализация PMF
Мы часто визуализируем массовые функции вероятности с помощью гистограмм.
Например, на следующей гистограмме показаны вероятности, связанные с количеством рождений в час для распределения Пуассона, описанного в предыдущем примере:
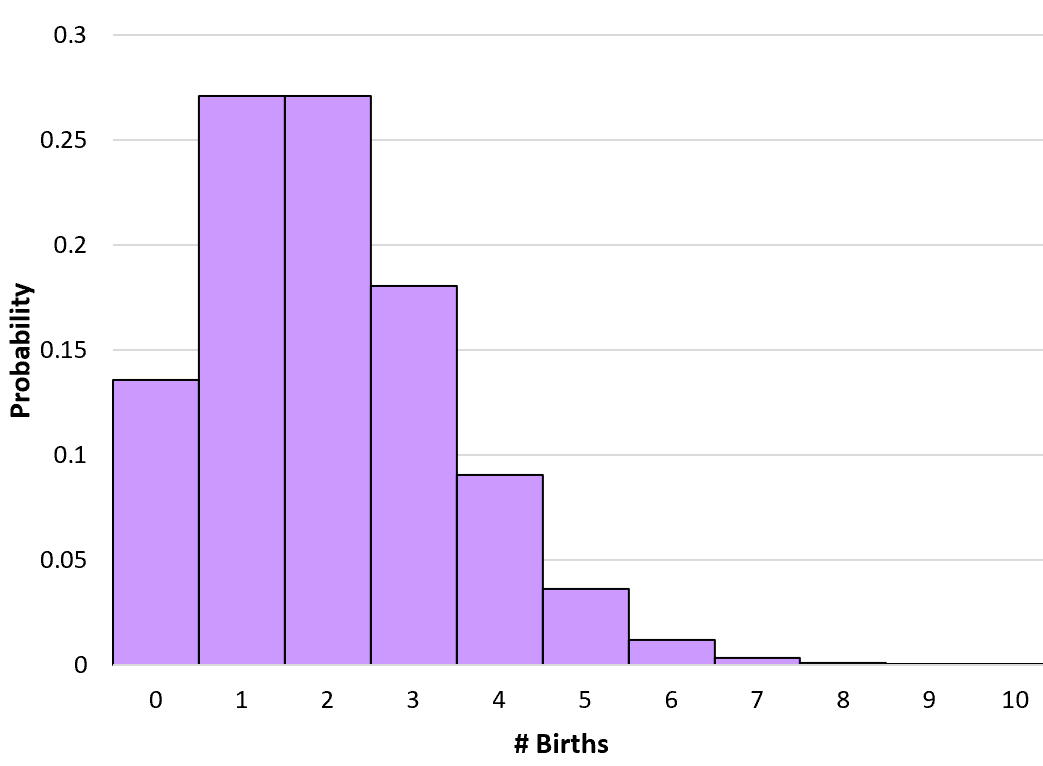
Обратите внимание, что количество рождений может достигать бесконечности, но вероятности становятся настолько низкими после 10, что мы даже не можем увидеть их на гистограмме.
Свойства PMF
Функция массы вероятности обладает следующими свойствами:
1. Все вероятности в опоре положительны. Например, вероятность того, что игральная кость выпадет между 1 и 6, положительна, а вероятность всех остальных результатов равна нулю.
2. Все результаты имеют вероятность от 0 до 1. Например, вероятность того, что игральная кость выпадет между 1 и 6, равна 1/6, или 0,1666666 для каждого результата.
3. Сумма всех вероятностей должна составлять 1. Например, сумма вероятностей того, что игральная кость выпадет на определенное число, равна 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.
Дополнительные ресурсы
Что такое случайные величины?
CDF и PDF: в чем разница?
Введение в биномиальное распределение
Введение в распределение Пуассона