Распределение Пуассона описывает вероятность получения k успехов за заданный интервал времени.
Если случайная величина X подчиняется распределению Пуассона, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = λk * e – λ / k !
куда:
- λ: среднее количество успехов за определенный интервал
- k: количество успехов
- e: константа, равная приблизительно 2,71828.
В этом руководстве объясняется, как использовать распределение Пуассона в Python.
Как сгенерировать распределение Пуассона
Вы можете использовать функцию poisson.rvs(mu, size) для генерации случайных значений из распределения Пуассона с определенным средним значением и размером выборки:
from scipy. stats import poisson
#generate random values from Poisson distribution with mean=3 and sample size=10
poisson. rvs (mu=3, size=10)
array([2, 2, 2, 0, 7, 2, 1, 2, 5, 5])
Как рассчитать вероятности, используя распределение Пуассона
Вы можете использовать функции poisson.pmf(k, mu) и poisson.cdf(k, mu) для вычисления вероятностей, связанных с распределением Пуассона.
Пример 1: Вероятность равна некоторому значению
Магазин продает в среднем 3 яблока в день. Какова вероятность того, что они продадут 5 яблок в данный день?
from scipy. stats import poisson
#calculate probability
poisson. pmf (k=5, mu=3)
0.100819
Вероятность того, что магазин продаст 5 яблок в данный день, равна 0,100819 .
Пример 2: Вероятность меньше некоторого значения
Один магазин продает в среднем семь футбольных мячей в день. Какова вероятность того, что этот магазин продаст четыре или меньше футбольных мячей в данный день?
from scipy. stats import poisson
#calculate probability
poisson. cdf (k=4, mu=7)
0.172992
Вероятность того, что магазин продаст четыре или меньше футбольных мячей в данный день, равна 0,172992 .
Пример 3: Вероятность больше некоторого значения
Один магазин продает в среднем 15 банок тунца в день. Какова вероятность того, что этот магазин продаст более 20 банок тунца в данный день?
from scipy. stats import poisson
#calculate probability
1-poisson. cdf (k=20, mu=15)
0.082971
Вероятность того, что магазин продаст более 20 банок тунца в данный день, равна 0,082971 .
Как построить распределение Пуассона
Вы можете использовать следующий синтаксис для построения распределения Пуассона с заданным средним значением:
from scipy. stats import poisson
import matplotlib.pyplot as plt
#generate Poisson distribution with sample size 10000
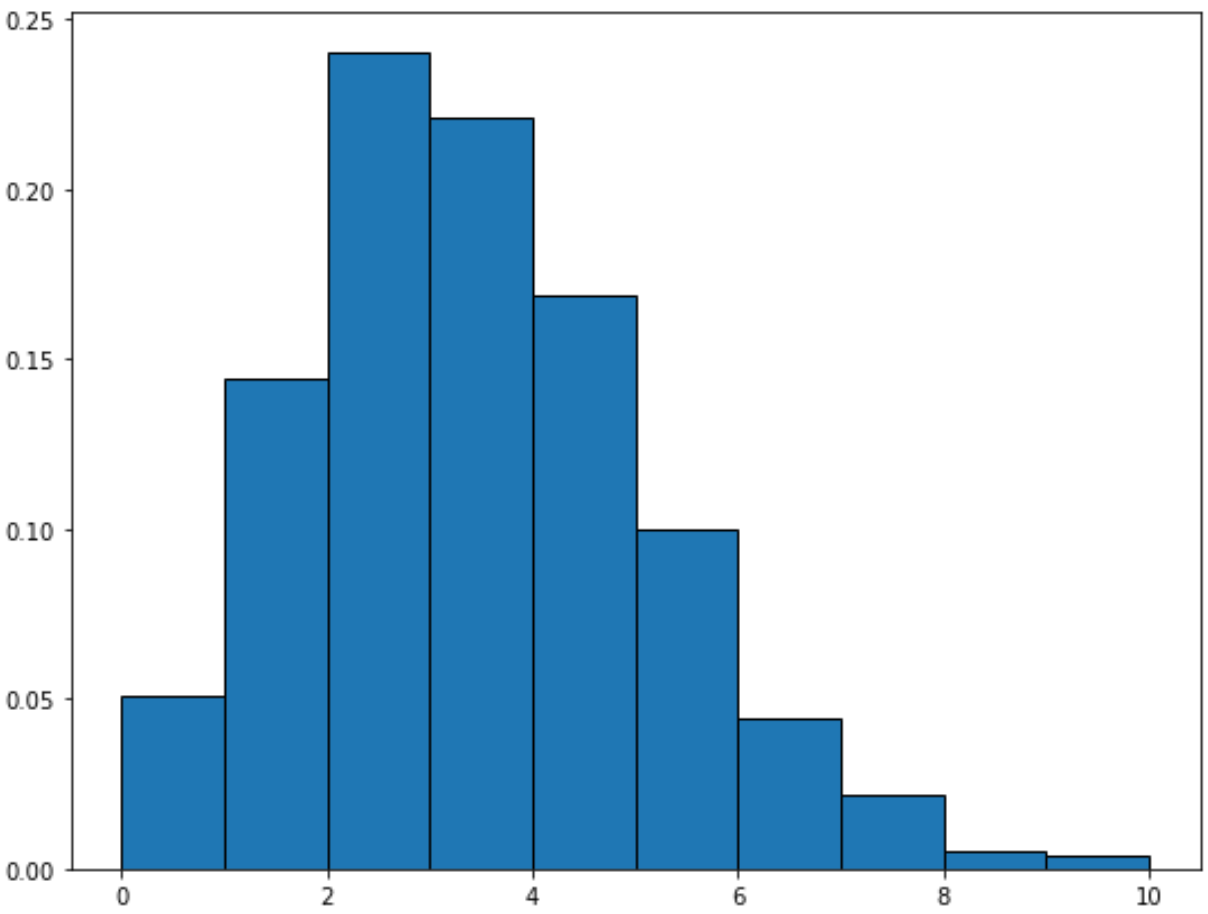
x = poisson. rvs (mu=3, size=10000)
#create plot of Poisson distribution
plt.hist (x, density= True , edgecolor='black')
Дополнительные ресурсы
Введение в распределение Пуассона
5 реальных примеров распределения Пуассона
Онлайн-калькулятор распределения Пуассона