В статистике ошибка прогнозирования относится к разнице между прогнозируемыми значениями, сделанными некоторой моделью, и фактическими значениями.
Ошибка прогноза часто используется в двух случаях:
1. Линейная регрессия: используется для прогнозирования значения некоторой переменной непрерывного отклика.
Обычно мы измеряем ошибку прогноза модели линейной регрессии с помощью метрики, известной как RMSE , что означает среднеквадратичную ошибку.
Он рассчитывается как:
СКО = √ Σ(ŷ i – y i ) 2 / n
куда:
- Σ — это символ, который означает «сумма»
- ŷ i - прогнозируемое значение для i -го наблюдения
- y i - наблюдаемое значение для i -го наблюдения
- n - размер выборки
2. Логистическая регрессия: используется для прогнозирования значения некоторой бинарной переменной отклика.
Одним из распространенных способов измерения ошибки прогнозирования модели логистической регрессии является метрика, известная как общий коэффициент ошибочной классификации.
Он рассчитывается как:
Общий коэффициент ошибочной классификации = (# неверных прогнозов / # всего прогнозов)
Чем ниже значение коэффициента ошибочной классификации, тем лучше модель способна предсказать результаты переменной отклика.
В следующих примерах показано, как на практике рассчитать ошибку прогнозирования как для модели линейной регрессии, так и для модели логистической регрессии.
Пример 1: Расчет ошибки прогноза в линейной регрессии
Предположим, мы используем регрессионную модель, чтобы предсказать количество очков, которое 10 игроков наберут в баскетбольном матче.
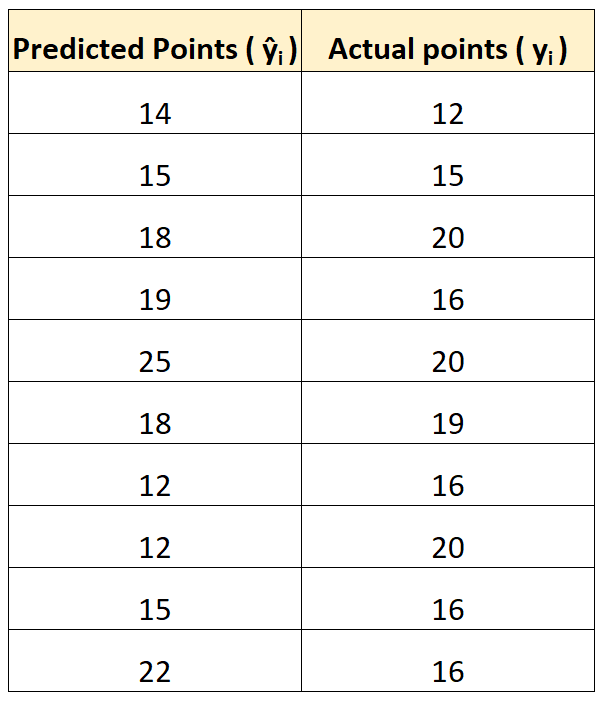
В следующей таблице показаны прогнозируемые очки по модели и фактические очки, набранные игроками:

Мы рассчитали бы среднеквадратичную ошибку (RMSE) как:
- СКО = √ Σ(ŷ i – y i ) 2 / n
- СКО = √(((14-12) 2 +(15-15) 2 +(18-20) 2 +(19-16) 2 +(25-20) 2 +(18-19) 2 +(12- 16) 2 +(12-20) 2 +(15-16) 2 +(22-16) 2 ) / 10)
- СКО = 4
Среднеквадратическая ошибка равна 4. Это говорит нам о том, что среднее отклонение между прогнозируемыми набранными баллами и фактическими набранными баллами равно 4.
Связанный: Что считается хорошим значением RMSE?
Пример 2: Расчет ошибки прогноза в логистической регрессии
Предположим, мы используем модель логистической регрессии, чтобы предсказать, попадут ли 10 баскетболистов из колледжа в НБА.
В следующей таблице показан прогнозируемый результат для каждого игрока по сравнению с фактическим результатом (1 = выбран на драфте, 0 = не выбран на драфте):

Мы рассчитали бы общий коэффициент ошибочной классификации как:
- Общий коэффициент ошибочной классификации = (# неверных прогнозов / # всего прогнозов)
- Общий коэффициент ошибочной классификации = 4/10
- Общий коэффициент ошибочной классификации = 40%
Общий уровень ошибочной классификации составляет 40% .
Это значение довольно велико, что указывает на то, что модель не очень хорошо предсказывает, будет ли игрок выбран на драфте.
Дополнительные ресурсы
Следующие руководства содержат введение в различные типы методов регрессии:
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Введение в логистическую регрессию