Выборочное распределение — это вероятностное распределение определенной статистики , основанное на множестве случайных выборок из одной совокупности.
В этом руководстве объясняется, как выполнить следующие действия с выборочными распределениями в R:
- Сгенерируйте выборочное распределение.
- Визуализируйте распределение выборки.
- Рассчитайте среднее значение и стандартное отклонение выборочного распределения.
- Рассчитайте вероятности относительно выборочного распределения.
Создание распределения выборки в R
В следующем коде показано, как сгенерировать выборочное распределение в R:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656
В этом примере мы использовали функцию rnorm() для вычисления среднего значения 10 000 выборок, в которых размер каждой выборки был равен 20 и был сгенерирован из нормального распределения со средним значением 5,3 и стандартным отклонением 9.
Мы видим, что первая выборка имела среднее значение 5,283992, вторая выборка имела среднее значение 6,304845 и так далее.
Визуализируйте распределение выборки
В следующем коде показано, как создать простую гистограмму для визуализации распределения выборки:
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means", col = " steelblue ")
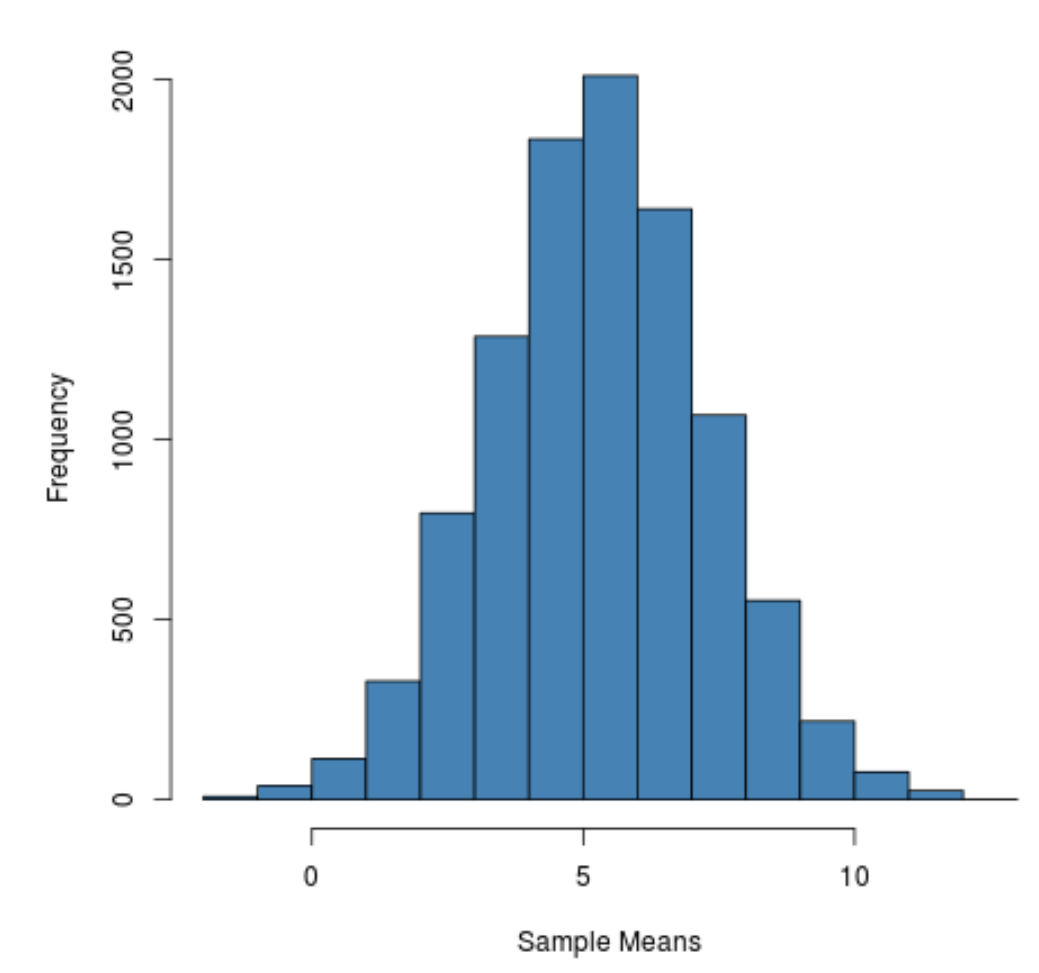
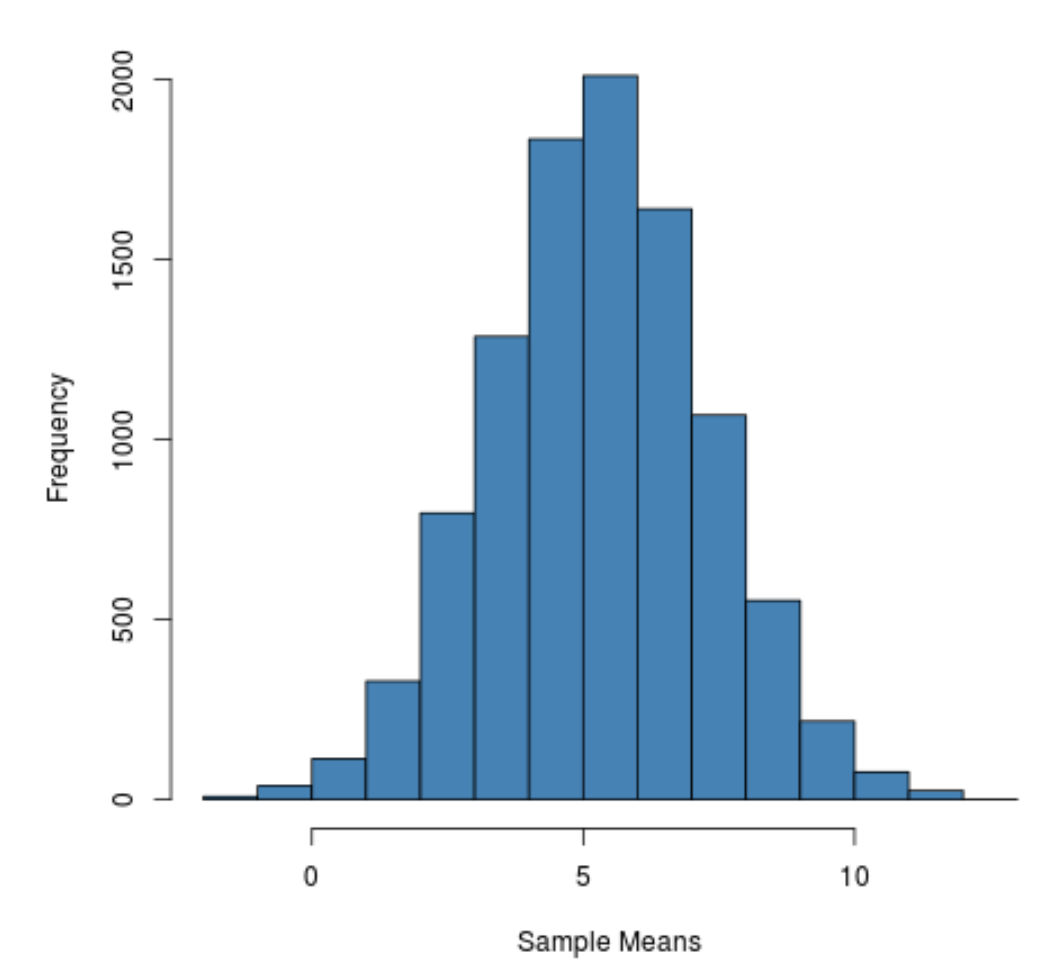
Мы видим, что распределение выборки имеет форму колокола с пиком около значения 5.
Однако из хвостов распределения мы можем видеть, что некоторые выборки имели средние значения больше 10, а некоторые — меньше 0.
Найдите среднее значение и стандартное отклонение
Следующий код показывает, как вычислить среднее значение и стандартное отклонение выборочного распределения:
#mean of sampling distribution
mean(sample_means)
[1] 5.287195
#standard deviation of sampling distribution
sd(sample_means)
[1] 2.00224
Теоретически среднее значение выборочного распределения должно быть 5,3. Мы видим, что фактическое среднее значение выборки в этом примере равно 5,287195 , что близко к 5,3.
И теоретически стандартное отклонение выборочного распределения должно быть равно s/√n, что будет равно 9/√20 = 2,012. Мы видим, что фактическое стандартное отклонение выборочного распределения составляет 2,00224 , что близко к 2,012.
Рассчитать вероятности
В следующем коде показано, как рассчитать вероятность получения определенного значения для среднего значения выборки на основе среднего значения совокупности, стандартного отклонения совокупности и размера выборки.
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
В этом конкретном примере мы находим вероятность того, что среднее значение выборки меньше или равно 6, учитывая, что среднее значение совокупности равно 5,3, стандартное отклонение совокупности равно 9, а размер выборки равен 20, что составляет 0,6417 .
Это очень близко к вероятности, рассчитанной Калькулятором распределения выборки :

Полный код
Полный код R, использованный в этом примере, показан ниже:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means", col = " steelblue ")
#mean of sampling distribution
mean(sample_means)
#standard deviation of sampling distribution
sd(sample_means)
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
Дополнительные ресурсы
Введение в выборочные распределения
Калькулятор распределения выборки
Введение в центральную предельную теорему