Тест Шапиро-Уилка используется для определения того, соответствует ли набор данных нормальному распределению .
В следующем пошаговом примере показано, как выполнить тест Шапиро-Уилка для набора данных в SAS.
Шаг 1: Создайте данные
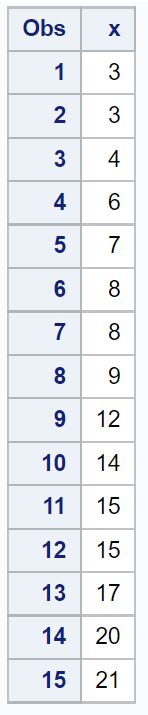
Сначала мы создадим набор данных, содержащий 15 наблюдений:
/\*create dataset\*/
data my_data;
input x;
datalines ;
3
3
4
6
7
8
8
9
12
14
15
15
17
20
21
;
run ;
/\*view dataset\*/
proc print data =my_data;

Шаг 2. Выполните тест Шапиро-Уилка.
Далее мы будем использовать proc univariate с командой normal для выполнения теста Шапиро-Уилка на нормальность:
/\*perform Shapiro-Wilk test\*/
proc univariate data =my_data normal ;
run ;
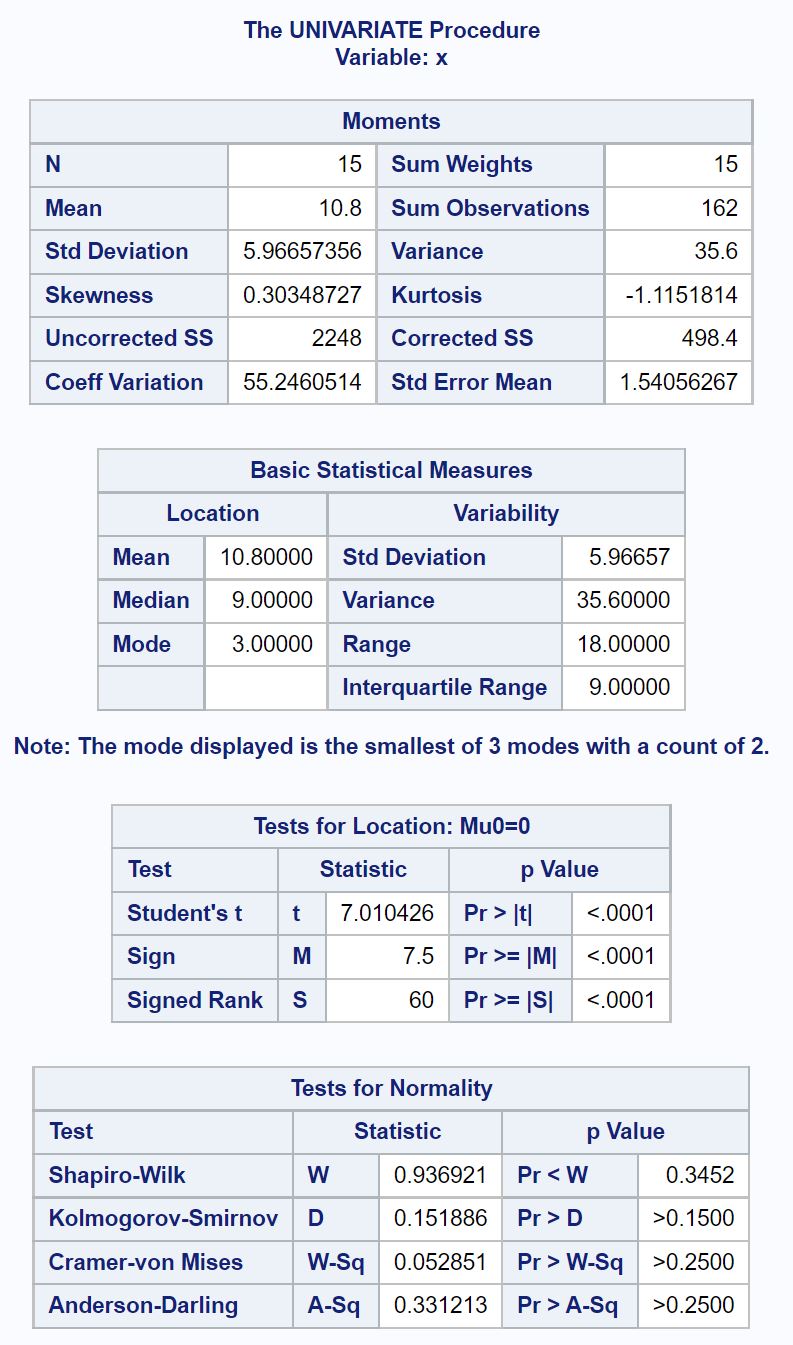
Вывод предоставляет нам массу информации, но единственная таблица, на которую нам нужно взглянуть, — это таблица под названием « Тесты на нормальность» .
В этой таблице представлены статистические данные испытаний и p-значения для нескольких тестов нормальности, включая:
- Тест Шапиро-Уилка
- Тест Колмогорова-Смирнова
- Тест Крамера-фон Мизеса
- Тест Андерсона-Дарлинга
Из этой таблицы видно, что значение p для теста Шапиро-Уилка составляет 0,3452 .
Напомним, что тест Шапиро-Уилка использует следующие нулевую и альтернативную гипотезы :
- H 0 : Данные нормально распределены.
- H A : Данные не распределены нормально.
Поскольку p-значение ( 0,3452 ) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
Это означает, что у нас нет достаточных доказательств того, что набор данных не имеет нормального распределения.
Другими словами, можно с уверенностью предположить, что набор данных нормально распределен.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные статистические тесты в SAS:
Как выполнить тест Колмогорова-Смирнова в SAS
Как выполнить критерий согласия хи-квадрат в SAS
Как выполнить точный тест Фишера в SAS