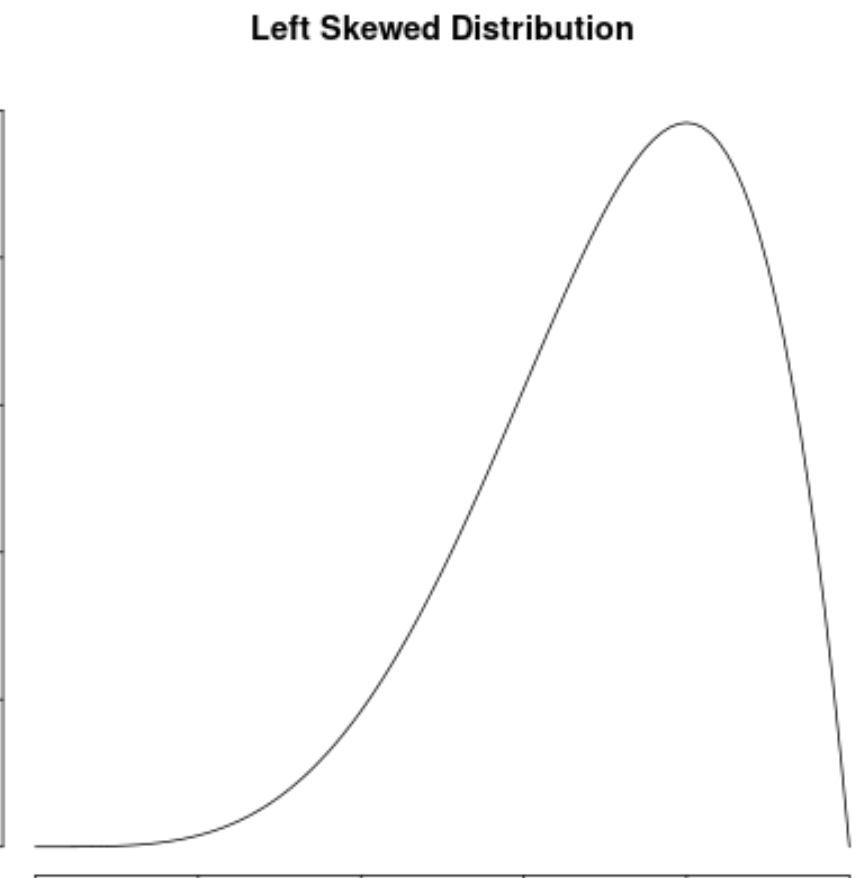
В области статистики мы используем асимметрию для описания симметрии распределения.
Мы говорим, что распределение значений данных асимметрично влево , если оно имеет «хвост» в левой части распределения:
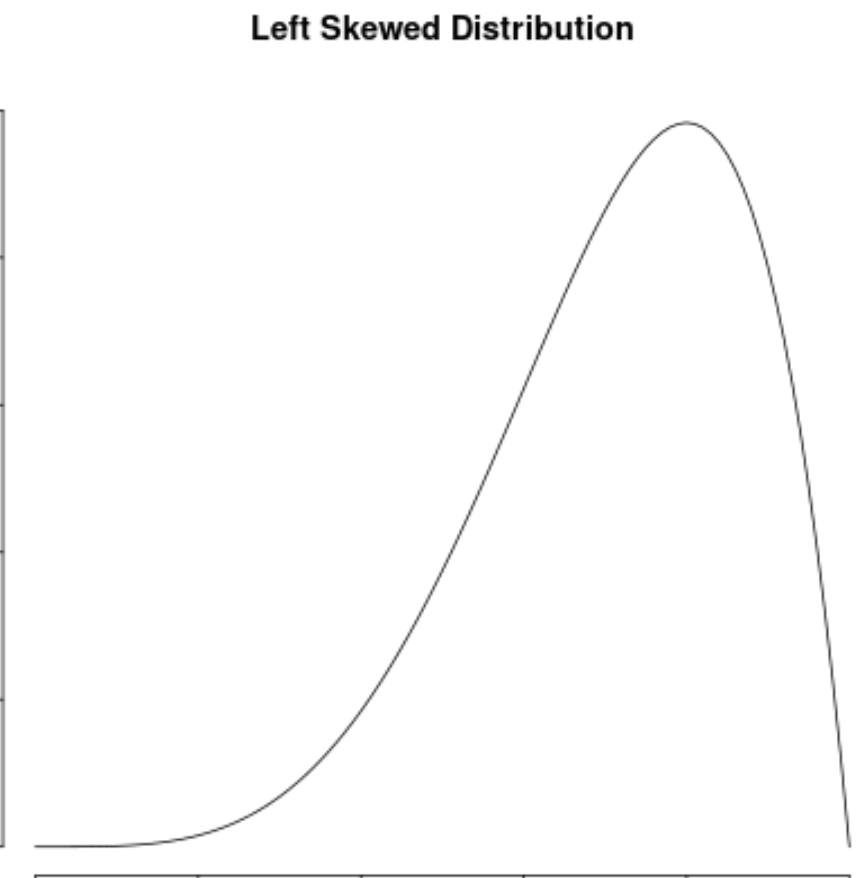
Мы говорим, что распределение скошено вправо , если оно имеет «хвост» в правой части распределения:
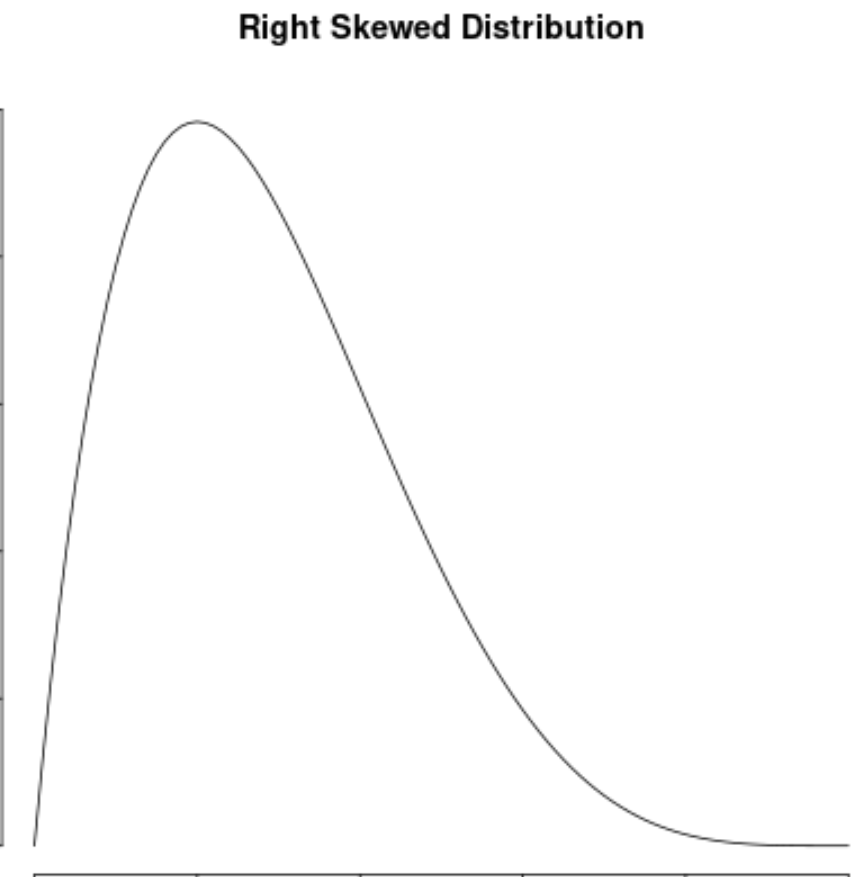
И мы говорим, что распределение не имеет перекоса , если оно симметрично с обеих сторон:
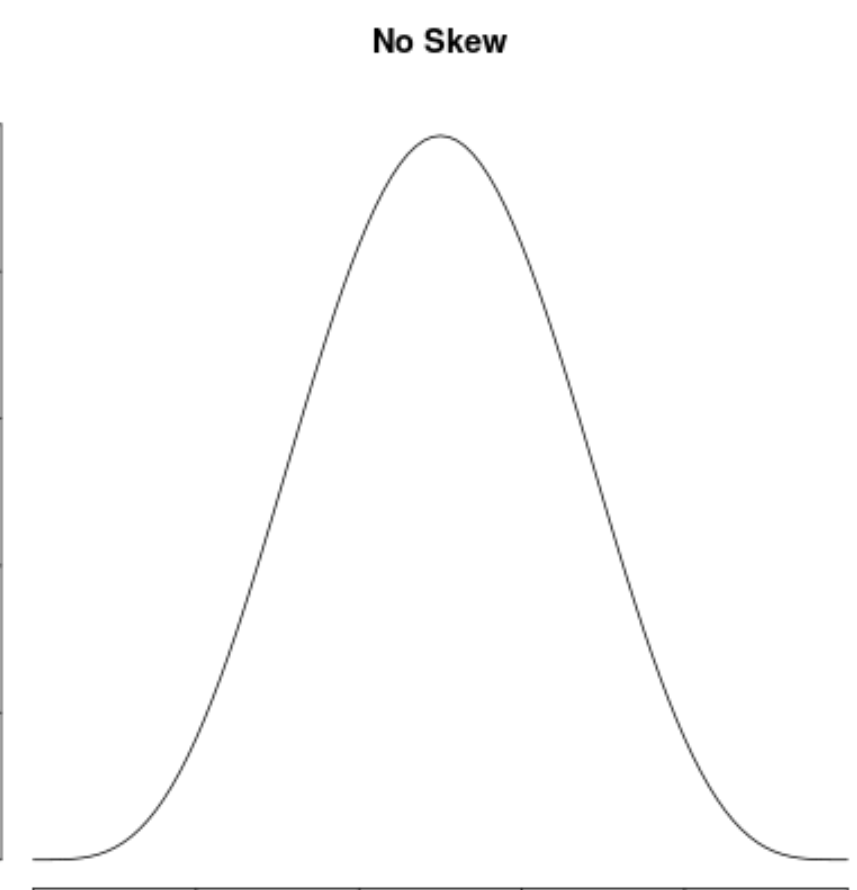
Как интерпретировать асимметрию
Значение асимметрии может варьироваться от отрицательной бесконечности до положительной бесконечности.
Вот как интерпретировать значения асимметрии:
- Отрицательное значение асимметрии указывает на то, что хвост находится в левой части распределения, которая простирается в сторону более отрицательных значений.
- Положительное значение асимметрии указывает на то, что хвост находится на правой стороне распределения, которая простирается в сторону более положительных значений.
- Нулевое значение указывает на то, что в распределении вообще нет асимметрии, что означает, что распределение совершенно симметрично.
В следующих примерах показано, как интерпретировать значения асимметрии на практике.
Пример 1: Распределение с асимметрией влево
Распределение возраста умерших в большинстве популяций асимметрично влево. Большинство людей доживает до 70–80 лет, и все меньше и меньше людей доживает до этого возраста.
Если бы мы создали график плотности , чтобы визуализировать распределение значений возраста смерти, он мог бы выглядеть примерно так:
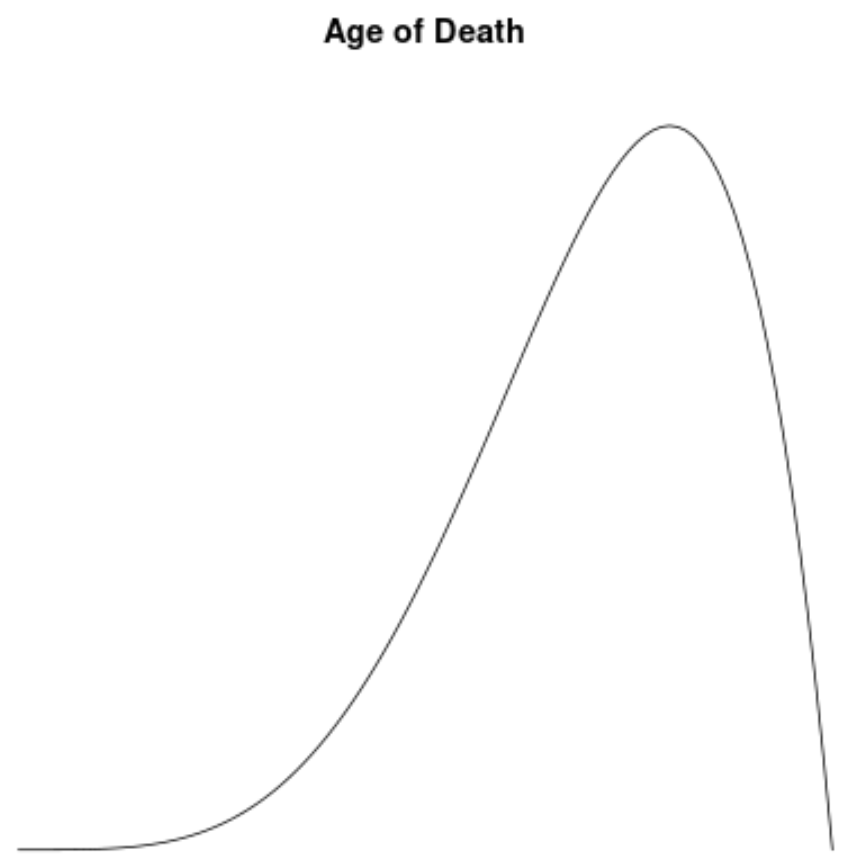
Предположим, мы вычисляем асимметрию для этого распределения и обнаруживаем, что она равна -1,3225 .
Поскольку это значение отрицательное, мы интерпретируем это как означающее, что распределение смещено влево, что означает, что хвост распространяется на левую часть распределения.
Пример 2: Правостороннее распределение
Распределение доходов домохозяйств в США смещено вправо: большинство домохозяйств зарабатывают от 30 до 70 тысяч долларов в год, но с длинным правым хвостом домохозяйств, которые зарабатывают гораздо больше.
Если бы мы создали график плотности, чтобы визуализировать распределение значений дохода домохозяйства, он мог бы выглядеть примерно так:
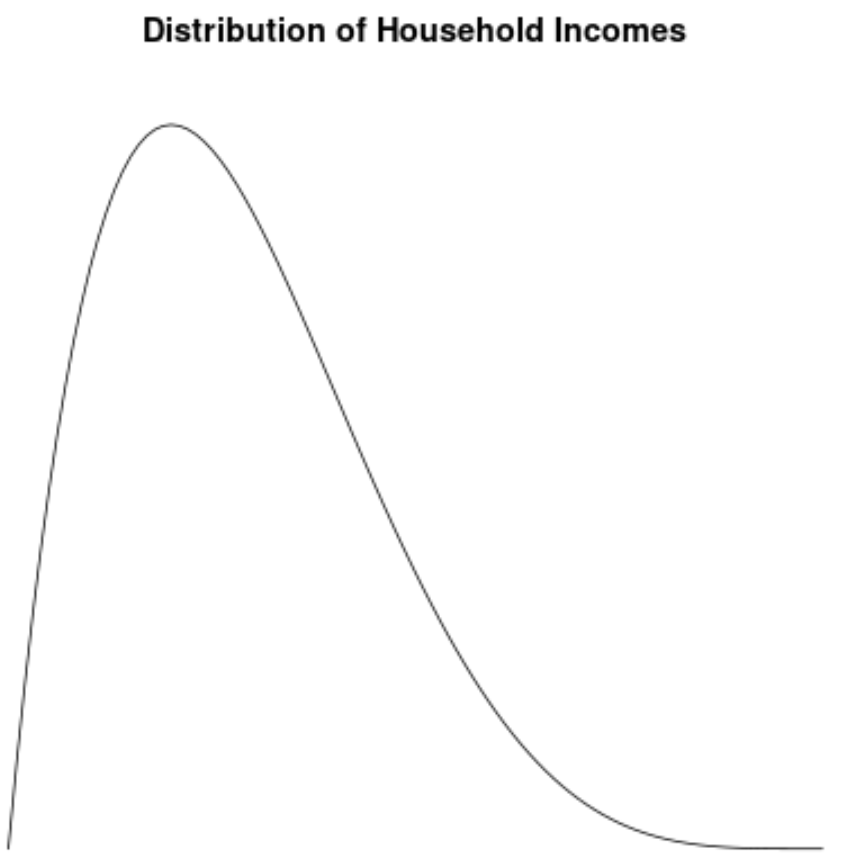
Предположим, мы вычисляем асимметрию для этого распределения и обнаруживаем, что она равна 2,0043 .
Поскольку это значение положительное, мы интерпретируем это как означающее, что распределение скошено вправо, что означает, что хвост распространяется на правую часть распределения.
Пример 3: Нет перекоса
Высота самцов примерно нормально распределена и не имеет перекоса. Например, средний рост мужчины в США составляет примерно 69,1 дюйма. Распределение высоты примерно симметрично: некоторые из них ниже, а некоторые выше.
Если бы мы создали график плотности, чтобы визуализировать распределение роста мужчин в США, он мог бы выглядеть примерно так:
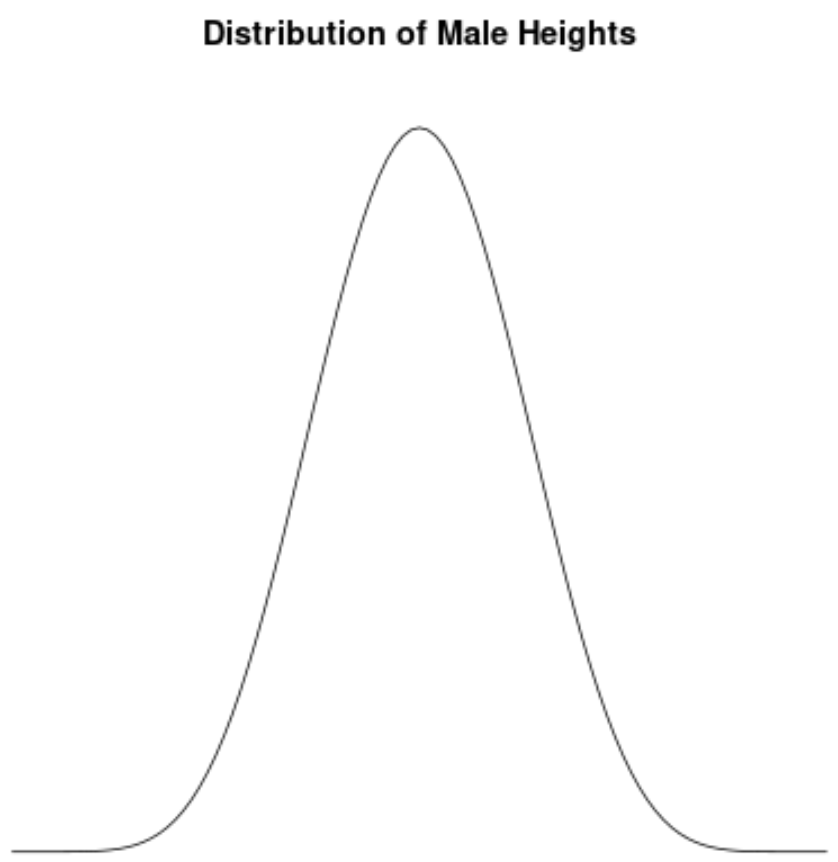
Предположим, мы вычисляем асимметрию для этого распределения и обнаруживаем, что она равна 0,0013 .
Поскольку это значение близко к нулю, мы интерпретируем это как означающее, что распределение практически не имеет перекоса, что означает, что хвосты с обеих сторон распределения примерно равны.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация об асимметрии в статистике:
5 примеров положительно асимметричных распределений
5 примеров распределения с отрицательным перекосом
Как рассчитать асимметрию в Excel
Как определить асимметрию в ящичковых диаграммах