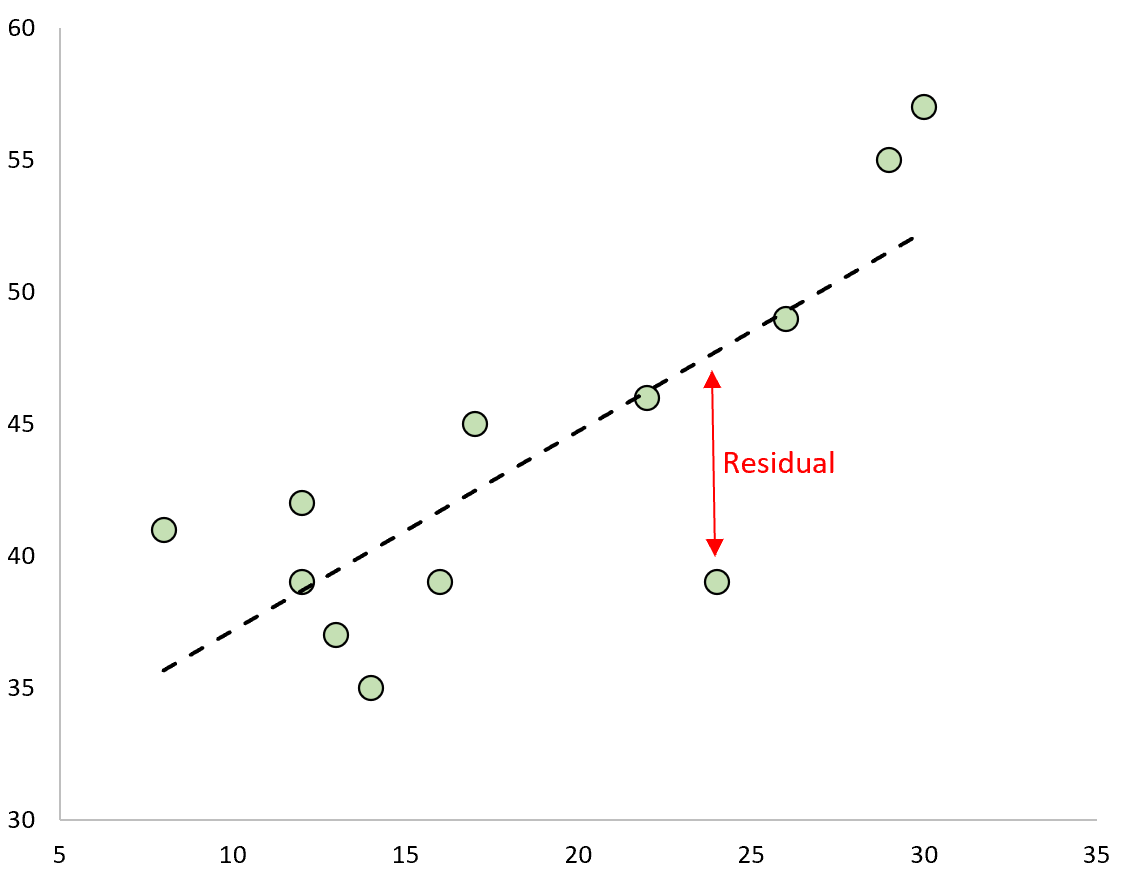
Остаток — это разница между наблюдаемым значением и прогнозируемым значением в регрессионной модели .
Он рассчитывается как:
Остаток = наблюдаемое значение – прогнозируемое значение
Если мы нанесем наблюдаемые значения и наложим подобранную линию регрессии, остатки для каждого наблюдения будут представлять собой расстояние по вертикали между наблюдением и линией регрессии:
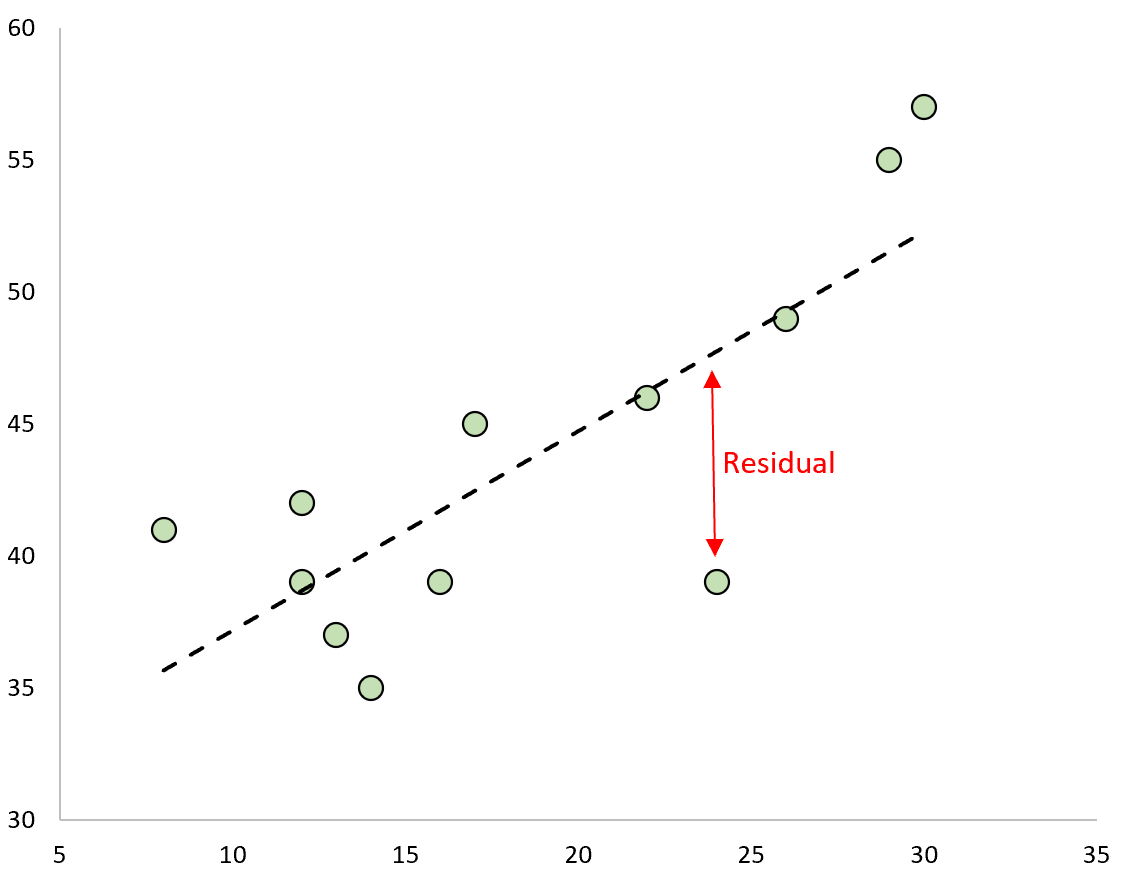
Один тип остатка, который мы часто используем для выявления выбросов в регрессионной модели, известен как стандартизированный остаток .
Он рассчитывается как:
r i = e i / s(e i ) = e i / RSE√ 1-h ii
куда:
- e i : i -й остаток
- RSE: остаточная стандартная ошибка модели.
- h ii : рычаг i -го наблюдения
На практике мы часто считаем выбросом любой стандартизованный остаток с абсолютным значением больше 3.
В этом руководстве представлен пошаговый пример расчета стандартизированных остатков в R.
Шаг 1: введите данные
Сначала мы создадим небольшой набор данных для работы в R:
#create data
data <- data.frame(x=c(8, 12, 12, 13, 14, 16, 17, 22, 24, 26, 29, 30),
y=c(41, 42, 39, 37, 35, 39, 45, 46, 39, 49, 55, 57))
#view data
data
x y
1 8 41
2 12 42
3 12 39
4 13 37
5 14 35
6 16 39
7 17 45
8 22 46
9 24 39
10 26 49
11 29 55
12 30 57
Шаг 2: Подгонка регрессионной модели
Далее мы будем использовать функцию lm() , чтобы подобрать простую модель линейной регрессии :
#fit model
model <- lm(y ~ x, data=data)
#view model summary
summary(model)
Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-8.7578 -2.5161 0.0292 3.3457 5.3268
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.6309 3.6189 8.188 9.6e-06 \*\*\*
x 0.7553 0.1821 4.148 0.00199 \*\*
---
Signif. codes: 0 ‘\*\*\*’ 0.001 ‘\*\*’ 0.01 ‘\*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.442 on 10 degrees of freedom
Multiple R-squared: 0.6324, Adjusted R-squared: 0.5956
F-statistic: 17.2 on 1 and 10 DF, p-value: 0.001988
Шаг 3: Рассчитайте стандартизированные остатки
Далее мы будем использовать встроенную функцию rstandard() для вычисления стандартизованных остатков модели:
#calculate the standardized residuals
standard_res <- rstandard(model)
#view the standardized residuals
standard_res
1 2 3 4 5 6
1.40517322 0.81017562 0.07491009 -0.59323342 -1.24820530 -0.64248883
7 8 9 10 11 12
0.59610905 -0.05876884 -2.11711982 -0.06655600 0.91057211 1.26973888
Мы можем добавить стандартизированные остатки обратно в исходный фрейм данных, если хотим:
#column bind standardized residuals back to original data frame
final_data <- cbind(data, standard_res)
#view data frame
x y standard_res
1 8 41 1.40517322
2 12 42 0.81017562
3 12 39 0.07491009
4 13 37 -0.59323342
5 14 35 -1.24820530
6 16 39 -0.64248883
7 17 45 0.59610905
8 22 46 -0.05876884
9 24 39 -2.11711982
10 26 49 -0.06655600
11 29 55 0.91057211
12 30 57 1.26973888
Затем мы можем отсортировать каждое наблюдение от наибольшего к наименьшему в соответствии с его стандартизированным остатком, чтобы получить представление о том, какие наблюдения ближе всего к выбросам:
#sort standardized residuals descending
final_data[ order (-standard_res),]
x y standard_res
1 8 41 1.40517322
12 30 57 1.26973888
11 29 55 0.91057211
2 12 42 0.81017562
7 17 45 0.59610905
3 12 39 0.07491009
8 22 46 -0.05876884
10 26 49 -0.06655600
4 13 37 -0.59323342
6 16 39 -0.64248883
5 14 35 -1.24820530
9 24 39 -2.11711982
Из результатов видно, что ни один из стандартизированных остатков не превышает абсолютного значения 3. Таким образом, ни одно из наблюдений не является выбросом.
Шаг 4: Визуализируйте стандартизированные остатки
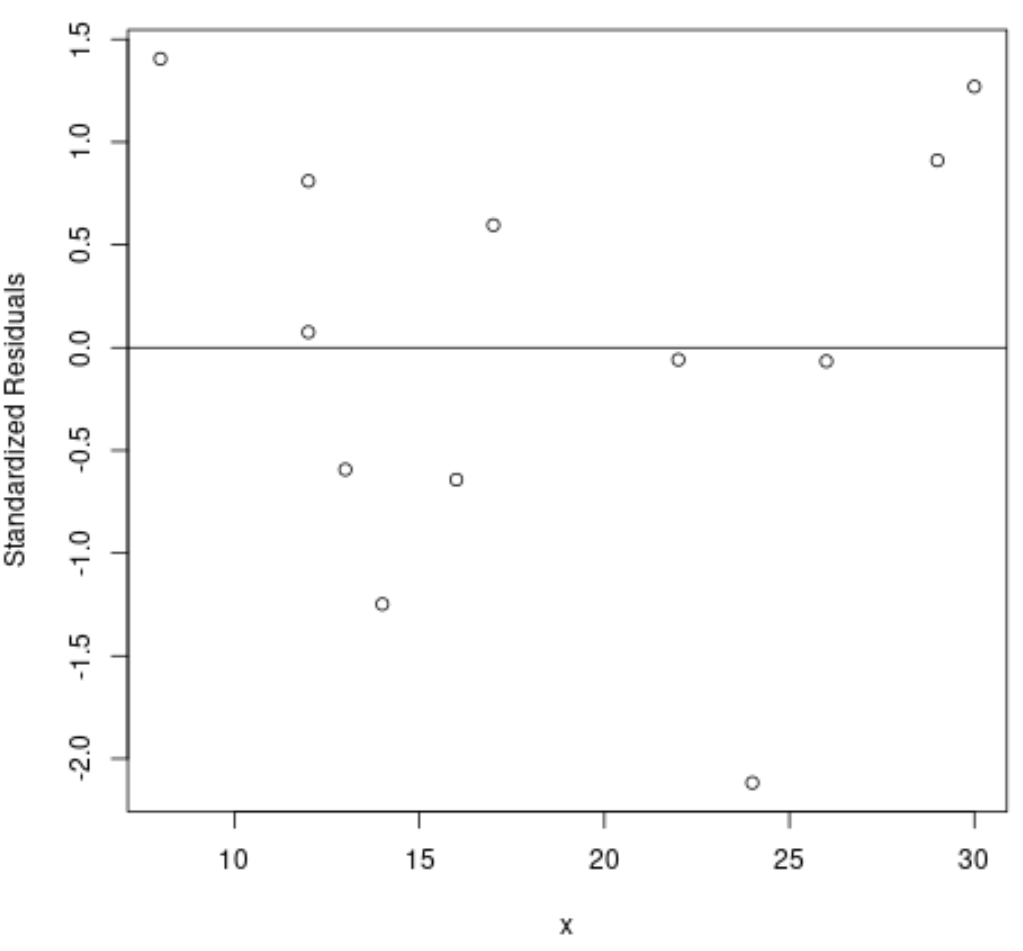
Наконец, мы можем создать диаграмму рассеяния, чтобы визуализировать значения переменной-предиктора по сравнению со стандартизованными остатками:
#plot predictor variable vs. standardized residuals
plot(final_data$x, standard_res, ylab='Standardized Residuals', xlab='x')
#add horizontal line at 0
abline(0, 0)
Дополнительные ресурсы
Что такое остатки?
Что такое стандартизированные остатки?
Введение в множественную линейную регрессию