Множественная линейная регрессия — полезный способ количественной оценки взаимосвязи между двумя или более переменными-предикторами и переменной- откликом .
Обычно, когда мы выполняем множественную линейную регрессию, результирующие коэффициенты регрессии нестандартизированы , то есть они используют необработанные данные для поиска линии наилучшего соответствия.
Однако, когда переменные-предикторы измеряются в совершенно разных масштабах, может быть полезно выполнить множественную линейную регрессию с использованием стандартизированных данных, что приводит к стандартизированным коэффициентам.
Чтобы помочь вам понять эту идею, давайте рассмотрим простой пример.
Пример: стандартизированные и нестандартизированные коэффициенты регрессии
Предположим, у нас есть следующий набор данных, который содержит информацию о возрасте, площади и цене продажи 12 домов:

Предположим, что затем мы выполняем множественную линейную регрессию, используя возраст и площадь в квадратных футах в качестве переменных-предикторов и цену в качестве переменной-отклика.Вот результат регрессии :

Коэффициенты регрессии в этой таблице нестандартизированы , то есть они использовали необработанные данные для соответствия этой модели регрессии. На первый взгляд кажется, что возраст оказывает гораздо большее влияние на цену дома, так как его коэффициент в таблице регрессии составляет -409,833 по сравнению со всего лишь 100,866 для предикторной переменной площади в квадратных футах .
Однако стандартная ошибка намного больше для возраста по сравнению с площадью в квадратных футах, поэтому соответствующее значение p на самом деле велико для возраста (p = 0,520) и мало для площади в квадратных футах (p = 0,000).
Причина крайних различий в коэффициентах регрессии заключается в крайних различиях в шкалах для двух переменных:
- Значения возраста варьируются от 4 до 44 лет.
- Значения квадратных метров варьируются от 1200 до 2800.
Предположим, что вместо этого мы стандартизируем исходные необработанные данные, преобразуя каждое значение исходных данных в z-оценку:
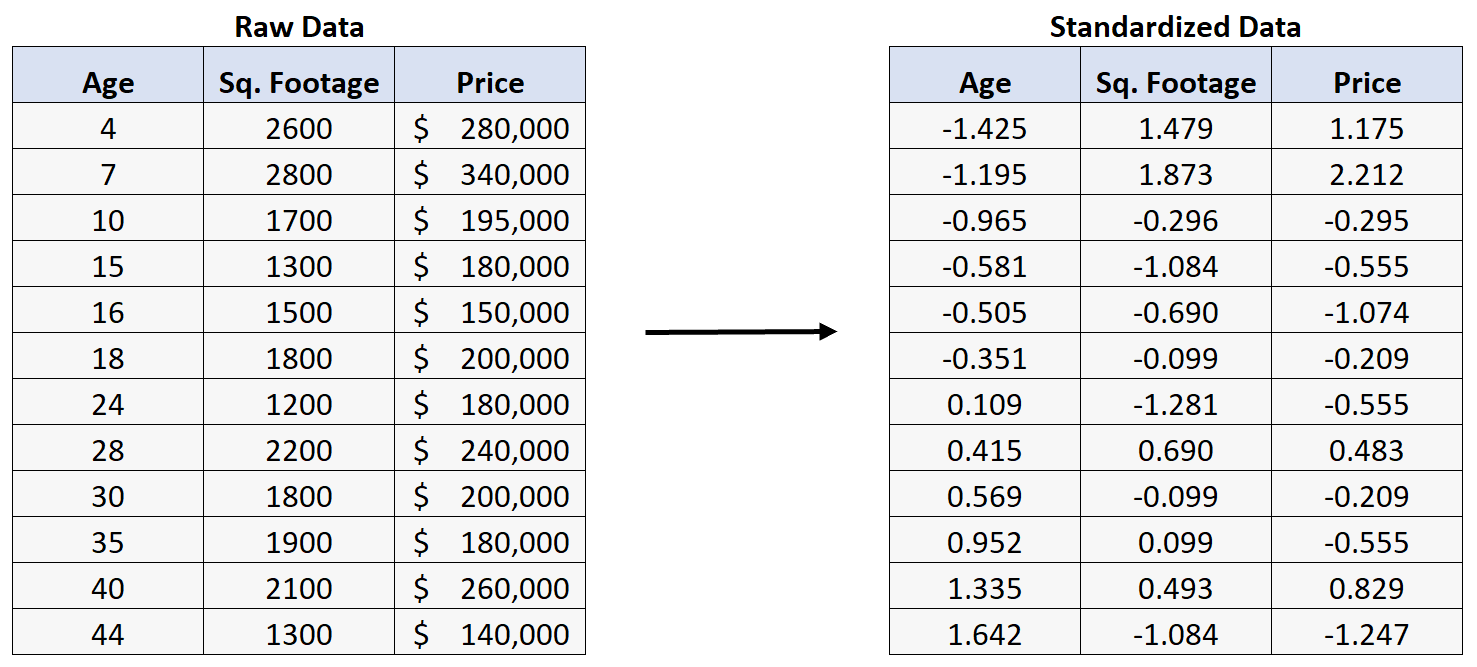
Если мы затем выполним множественную линейную регрессию, используя стандартизированные данные, мы получим следующий результат регрессии:

Коэффициенты регрессии в этой таблице стандартизированы , то есть они использовали стандартизированные данные для соответствия этой модели регрессии. Способ интерпретации коэффициентов в таблице следующий:
- Увеличение возраста на одно стандартное отклонение связано со снижением стоимости дома на 0,92 стандартного отклонения, при условии, что площадь в квадратных футах остается неизменной.
- Увеличение площади в квадратных футах на одно стандартное отклонение связано с увеличением стоимости дома на 0,885 стандартного отклонения, если предположить, что возраст остается постоянным.
Сразу видно, что квадратные метры оказывают гораздо большее влияние на цену дома, чем возраст. Также обратите внимание, что p-значения для каждой переменной-предиктора точно такие же, как и в предыдущей модели регрессии.
Связанный: Как рассчитать Z-баллы в Excel
Когда использовать стандартизированные и нестандартизированные коэффициенты регрессии
В зависимости от ситуации могут быть полезны как стандартизированные, так и нестандартизированные коэффициенты регрессии. Особенно:
Нестандартизированные коэффициенты регрессии полезны, когда вы хотите интерпретировать эффект, который изменение на одну единицу переменной предиктора оказывает на переменную отклика. В приведенном выше примере мы могли бы использовать нестандартизированные коэффициенты регрессии из первой регрессии, чтобы понять точную связь между переменными-предикторами и переменной ответа:
- Увеличение возраста на одну единицу было связано со снижением цены дома в среднем на 409 долларов , если предположить, что площадь в квадратных футах остается неизменной. Этот коэффициент оказался статистически недостоверным (р=0,520).
- Увеличение площади на одну единицу было связано с увеличением цены дома в среднем на 100 долларов , если предположить, что возраст оставался постоянным. Этот коэффициент также оказался статистически значимым (р=0,000).
Стандартизированные коэффициенты регрессии полезны, когда вы хотите сравнить влияние различных переменных-предикторов на переменную отклика. Поскольку каждая переменная стандартизирована, вы можете увидеть, какая переменная оказывает наибольшее влияние на переменную ответа.
Одним из недостатков стандартизированных коэффициентов регрессии является то, что их немного сложнее интерпретировать. Например, легче понять влияние увеличения возраста на одну единицу на цену дома по сравнению с влиянием увеличения на одну единицу стандартного отклонения на цену дома.
Дополнительные ресурсы
Как читать и интерпретировать таблицу регрессии
Как интерпретировать коэффициенты регрессии
Как выполнить множественную линейную регрессию в Excel


