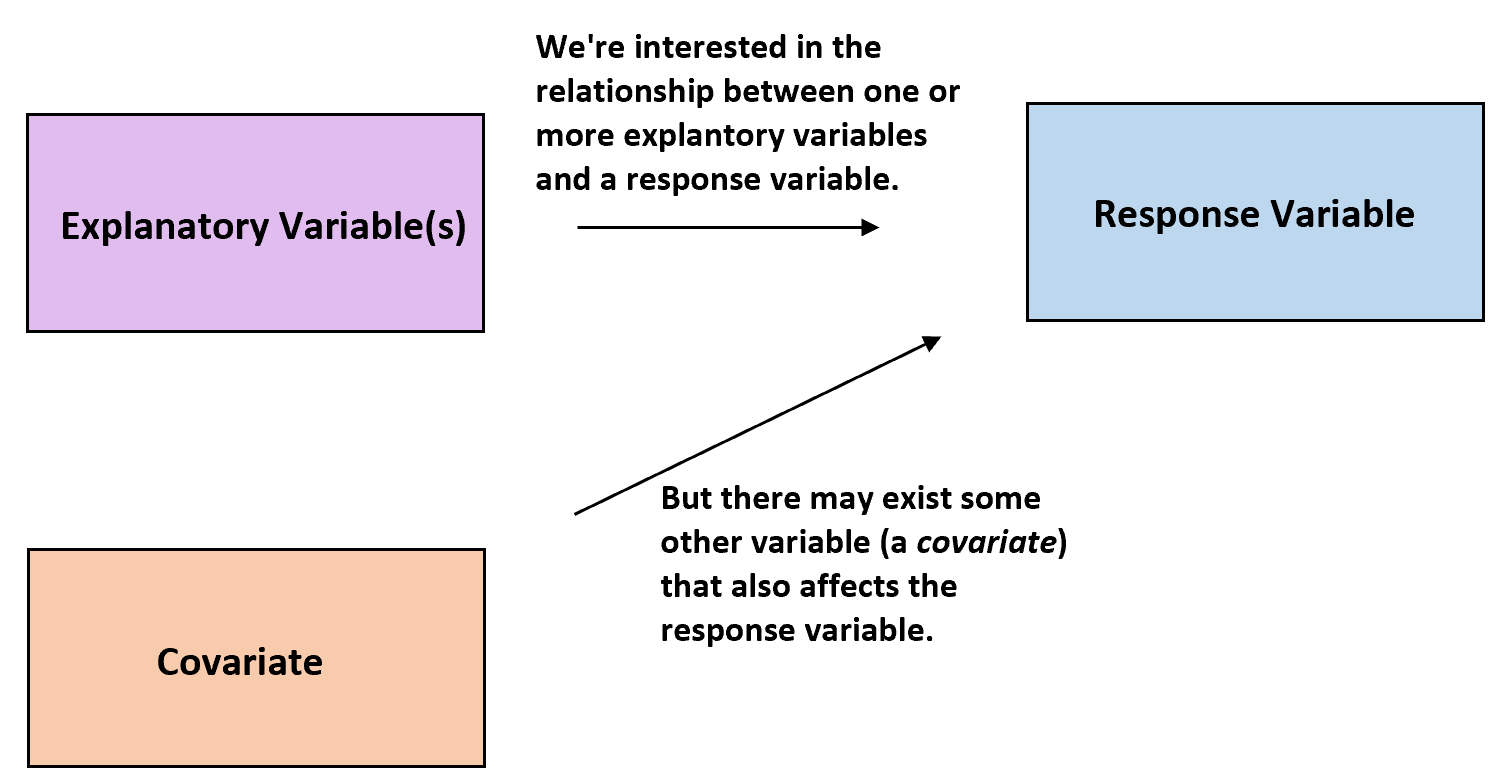
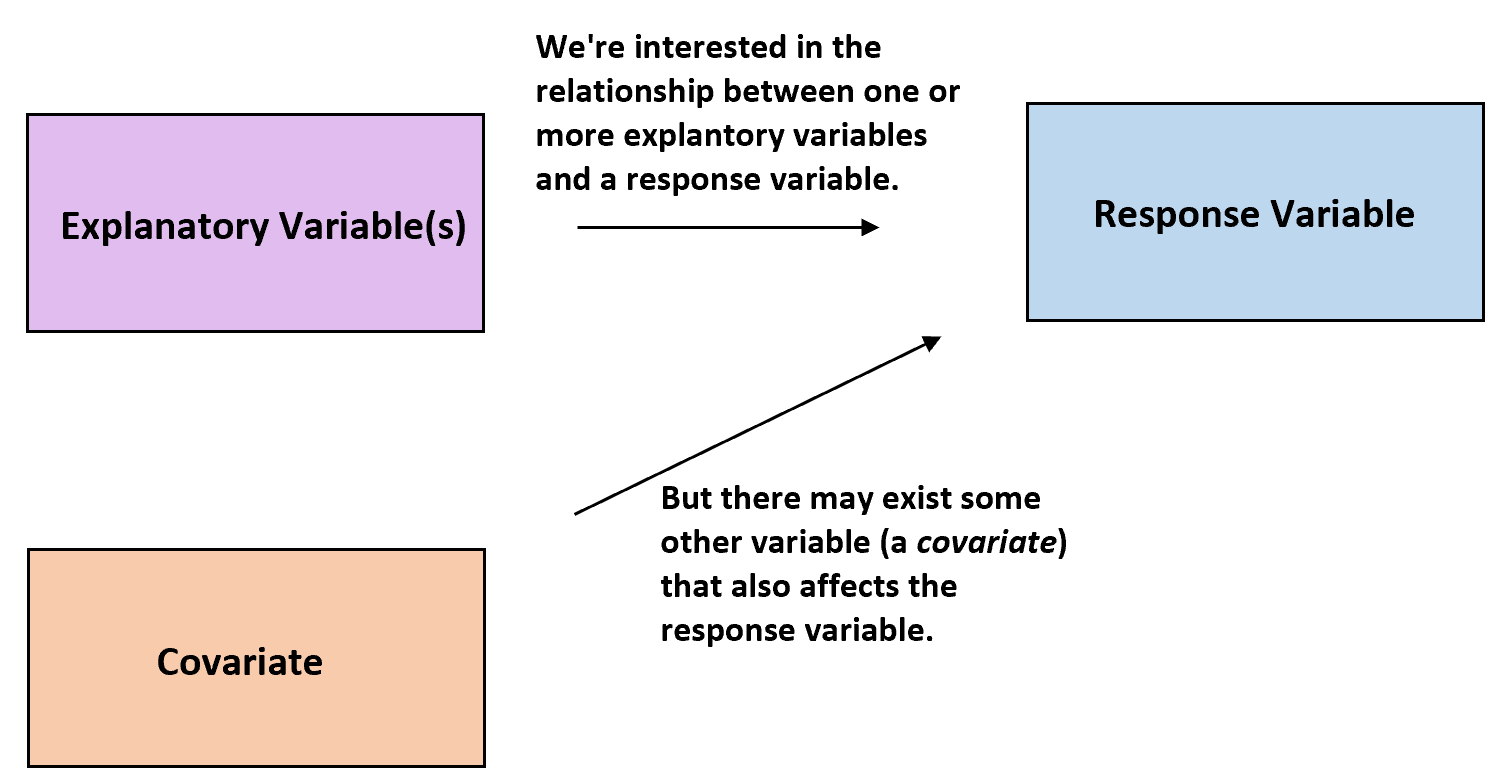
В статистике исследователи часто интересуются взаимосвязью между одной или несколькими объясняющими переменными и переменной отклика .
Однако иногда могут быть и другие переменные, которые могут повлиять на переменную отклика, не представляющую интереса для исследователей. Эти переменные известны как ковариаты .
Ковариаты: переменные, которые влияют на переменную отклика, но не представляют интереса для исследования.
Например, предположим, исследователи хотят знать, приводят ли три разных метода обучения к разным средним баллам на экзаменах в определенной школе. Методика обучения является объясняющей переменной, а экзаменационная оценка — переменной ответа.
Тем не менее, должны существовать некоторые различия в учебных способностях учащихся в трех группах. Если это не учитывать, это будет необъяснимой вариацией в рамках исследования, и будет труднее увидеть истинную взаимосвязь между техникой обучения и экзаменационным баллом.
Одним из способов учета этого может быть использование текущей оценки учащегося в классе в качестве ковариации.Хорошо известно, что текущая оценка учащегося, вероятно, коррелирует с его будущими баллами на экзаменах.
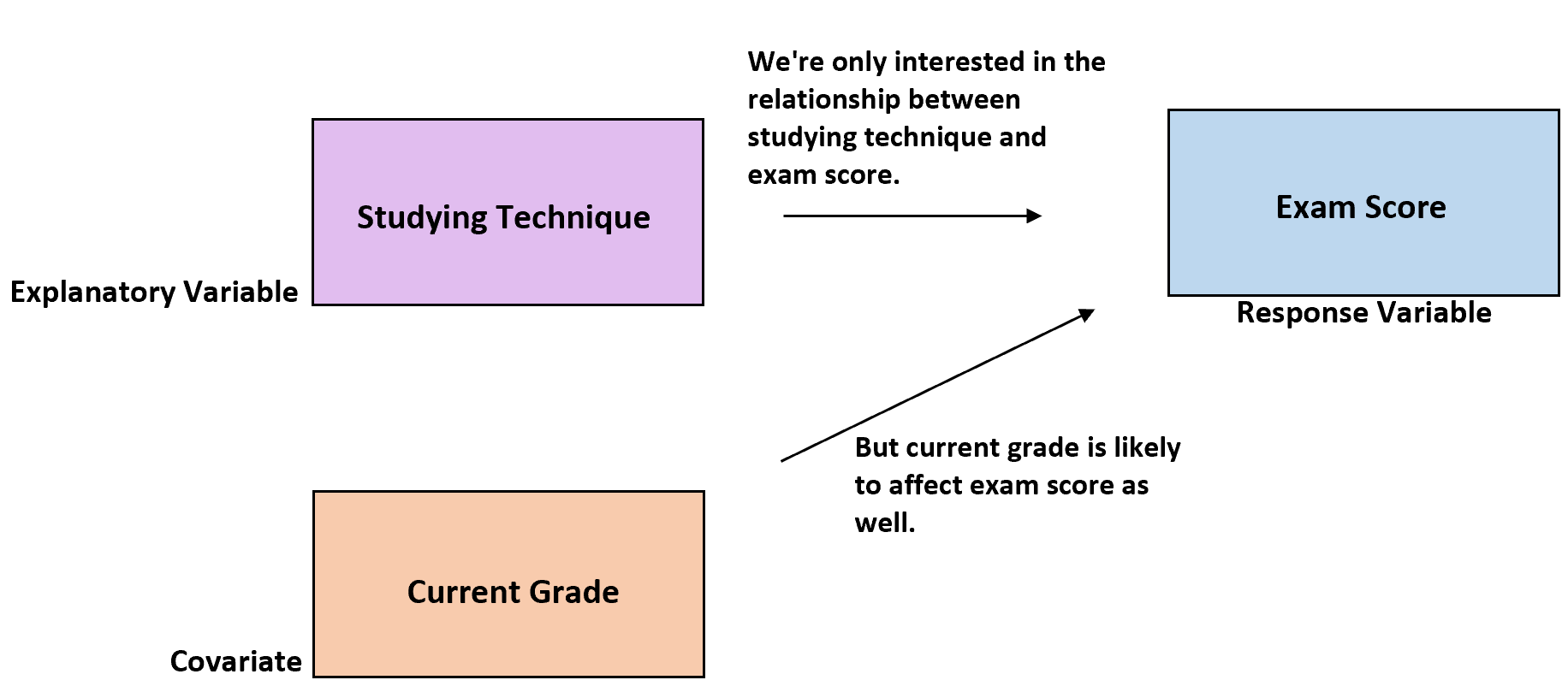
Таким образом, хотя текущая оценка не представляет интереса для данного исследования, ее можно включить в качестве ковариации, чтобы исследователи могли видеть, влияет ли изучение техники на экзаменационные баллы даже после учета текущей оценки учащегося в классе.
Ковариаты чаще всего появляются в двух типах параметров: ANOVA (дисперсионный анализ) и регрессия.
Ковариаты в ANOVA
Когда мы выполняем дисперсионный анализ (будь то однофакторный дисперсионный анализ , двусторонний дисперсионный анализ или что-то более сложное), мы заинтересованы в том, чтобы выяснить, существует ли разница между средними значениями трех или более независимых групп.
В нашем предыдущем примере нас интересовало, есть ли разница в средних экзаменационных баллах между тремя разными методами обучения. Чтобы понять это, мы могли бы провести односторонний ANOVA.
Однако, поскольку мы знали, что текущая оценка учащегося также может повлиять на результаты экзаменов, мы могли включить ее в качестве ковариации и вместо этого выполнить ANCOVA (анализ ковариации).
Это похоже на дисперсионный анализ, за исключением того, что мы включаем непрерывную переменную (текущая оценка учащегося) в качестве ковариации , чтобы мы могли понять, есть ли разница в средних экзаменационных баллах между тремя методами обучения, даже после учета успеваемости учащегося. текущий класс .
Ковариаты в регрессии
Когда мы выполняем линейную регрессию, нас интересует количественная оценка взаимосвязи между одной или несколькими независимыми переменными и переменной отклика.
Например, мы могли бы запустить простую линейную регрессию , чтобы количественно определить взаимосвязь между площадью в квадратных футах и ценами на жилье в определенном городе. Однако может быть известно, что возраст дома также является переменной, влияющей на цену дома.
В частности, более старые дома могут быть связаны с более низкими ценами на жилье. В этом случае возраст дома будет ковариантой , поскольку мы на самом деле не заинтересованы в его изучении, но знаем, что он влияет на цену дома.
Таким образом, мы могли бы включить возраст дома в качестве объясняющей переменной и запустить множественную линейную регрессию с площадью и возрастом дома в качестве объясняющих переменных и ценой дома в качестве переменной отклика.
Таким образом, коэффициент регрессии для площади в квадратных футах покажет нам среднее изменение цены дома, связанное с увеличением площади на одну единицу после учета возраста дома .
Дополнительные ресурсы
Введение в ANCOVA (дисперсионный анализ)
Как интерпретировать коэффициенты регрессии
Как выполнить ANCOVA в Excel
Как выполнить множественную линейную регрессию в Excel