Многие статистические тесты делают предположение о равной дисперсии.Если это допущение нарушается, то результаты испытаний становятся недостоверными.
Наиболее распространенные статистические тесты и процедуры, которые делают это предположение о равной дисперсии, включают:
1. Дисперсионный анализ
2. t-тесты
3. Линейная регрессия
В этом руководстве объясняется предположение, сделанное для каждого теста, как определить, выполняется ли это предположение, и что делать, если оно нарушается.
Предположение о равной дисперсии в ANOVA
ANOVA («Дисперсионный анализ») используется для определения того, существует ли значительная разница между средними значениями трех или более независимых групп.
Вот пример того, когда мы могли бы использовать ANOVA:
Предположим, мы набираем 90 человек для участия в эксперименте по снижению веса. Мы случайным образом назначаем 30 человек для использования программы A, B или C в течение одного месяца.
Чтобы увидеть, влияет ли программа на потерю веса, мы можем выполнить односторонний ANOVA .
ANOVA предполагает, что каждая из групп имеет одинаковую дисперсию. Есть два способа проверить, выполняется ли это предположение:
1. Создайте блокплоты.
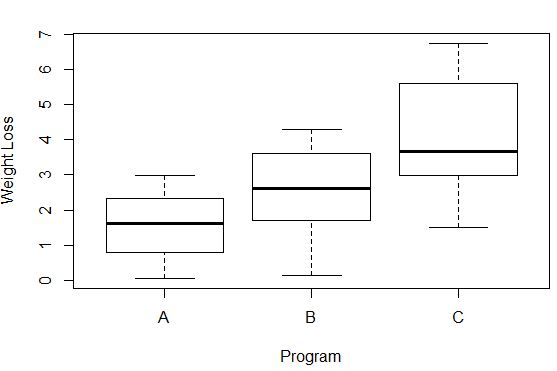
Блочные диаграммы предлагают визуальный способ проверить предположение о равных дисперсиях.
Дисперсия потери веса в каждой группе может быть видна по длине каждого квадратичного графика. Чем длиннее коробка, тем выше дисперсия. Например, мы видим, что дисперсия немного выше для участников программы C по сравнению с программой A и программой B.
2. Проведите тест Бартлетта.
Тест Бартлетта проверяет нулевую гипотезу о том, что выборки имеют одинаковую дисперсию, по сравнению с альтернативной гипотезой о том, что выборки не имеют одинаковой дисперсии.
Если p-значение теста меньше некоторого уровня значимости (например, 0,05), то у нас есть основания говорить о том, что не все выборки имеют одинаковую дисперсию.
Что, если предположение о равной дисперсии нарушается?
В целом ANOVA считается достаточно устойчивым к нарушениям предположения о равных дисперсиях, если каждая группа имеет одинаковый размер выборки.
Однако, если размеры выборки неодинаковы и это допущение серьезно нарушено, вы можете вместо этого запустить критерий Крускала-Уоллиса , который является непараметрической версией однофакторного дисперсионного анализа.
Предположение о равной дисперсии в t-тестах
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.
Тест делает предположение, что дисперсии равны между двумя группами. Есть два способа проверить, выполняется ли это предположение:
1. Используйте эмпирическое соотношение.
Как правило, если отношение большей дисперсии к меньшей дисперсии меньше 4, то мы можем предположить, что дисперсии примерно равны, и использовать двухвыборочный t-критерий.
Например, предположим, что выборка 1 имеет дисперсию 24,5, а выборка 2 — 15,2. Отношение большей дисперсии выборки к меньшей дисперсии выборки будет рассчитано как 24,5 / 15,2 = 1,61.
Поскольку это отношение меньше 4, можно предположить, что дисперсии между двумя группами примерно равны.
2. Выполните F-тест.
F-тест проверяет нулевую гипотезу о том, что выборки имеют равные дисперсии, по сравнению с альтернативной гипотезой о том, что выборки не имеют одинаковых дисперсий.
Если p-значение теста меньше некоторого уровня значимости (например, 0,05), то у нас есть основания говорить о том, что не все выборки имеют одинаковую дисперсию.
Что, если предположение о равной дисперсии нарушается?
Если это предположение нарушается, мы можем выполнить t-критерий Уэлча , который является непараметрической версией t-критерия для двух выборок и не предполагает, что две выборки имеют одинаковые дисперсии.
Предположение о равной дисперсии в линейной регрессии
Линейная регрессия используется для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика.
Линейная регрессия предполагает, что остатки имеют постоянную дисперсию на каждом уровне предикторов. Это известно как гомоскедастичность.Когда это не так, говорят, что остатки страдают от гетероскедастичности , и результаты регрессионного анализа становятся ненадежными.
Наиболее распространенный способ определить, выполняется ли это предположение, — построить график остатков по сравнению с подобранными значениями. Если остатки на этом графике кажутся случайным образом разбросанными вокруг нуля, то предположение о гомоскедастичности, вероятно, выполняется.
Однако, если в остатках существует систематическая закономерность, такая как форма «конуса» на следующем графике, тогда гетероскедастичность является проблемой:

Что, если предположение о равной дисперсии нарушается?
Если это предположение нарушается, наиболее распространенный способ справиться с этим — преобразовать переменную ответа с помощью одного из трех преобразований:
1. Преобразование журнала: преобразование переменной ответа из y в log(y) .
2. Преобразование квадратного корня: преобразовать переменную отклика из y в √ y .
3. Преобразование кубического корня: преобразовать переменную ответа из y в y 1/3 .
При выполнении этих преобразований проблема гетероскедастичности обычно исчезает.
Другой способ исправить гетероскедастичность состоит в использовании взвешенной регрессии наименьших квадратов.Этот тип регрессии присваивает вес каждой точке данных на основе дисперсии ее подобранного значения.
По сути, это дает небольшие веса точкам данных с более высокой дисперсией, что уменьшает их квадраты невязок. Когда используются правильные веса, это может устранить проблему гетероскедастичности.
Дополнительные ресурсы
Три предположения, сделанные в ANOVA
Четыре предположения, сделанные в Т-тесте
Четыре допущения линейной регрессии