Одно из ключевых предположений линейной регрессии состоит в том, что остатки распределяются с одинаковой дисперсией на каждом уровне предиктора. Это предположение известно как гомоскедастичность .
Когда это предположение нарушается, говорят, что в остатках присутствует гетероскедастичность.Когда это происходит, результаты регрессии становятся ненадежными.
Один из способов решения этой проблемы — вместо этого использовать взвешенную регрессию наименьших квадратов , которая присваивает веса наблюдениям таким образом, что наблюдениям с небольшой дисперсией ошибки присваивается больший вес, поскольку они содержат больше информации по сравнению с наблюдениями с большей дисперсией ошибки.
В этом руководстве представлен пошаговый пример выполнения регрессии методом наименьших квадратов веса в R.
Шаг 1: Создайте данные
Следующий код создает фрейм данных, который содержит количество часов обучения и соответствующий результат экзамена для 16 студентов:
df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))
Шаг 2: выполните линейную регрессию
Далее мы воспользуемся функцией lm() , чтобы подобрать простую модель линейной регрессии , в которой часы используются в качестве переменной-предиктора, а оценка — в качестве переменной-ответа :
#fit simple linear regression model
model <- lm(score ~ hours, data = df)
#view summary of model
summary(model)
Call:
lm(formula = score ~ hours, data = df)
Residuals:
Min 1Q Median 3Q Max
-17.967 -5.970 -0.719 7.531 15.032
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 60.467 5.128 11.791 1.17e-08 \*\*\*
hours 5.500 1.127 4.879 0.000244 \*\*\*
---
Signif. codes: 0 ‘\*\*\*’ 0.001 ‘\*\*’ 0.01 ‘\*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438
Шаг 3: Тест на гетероскедастичность
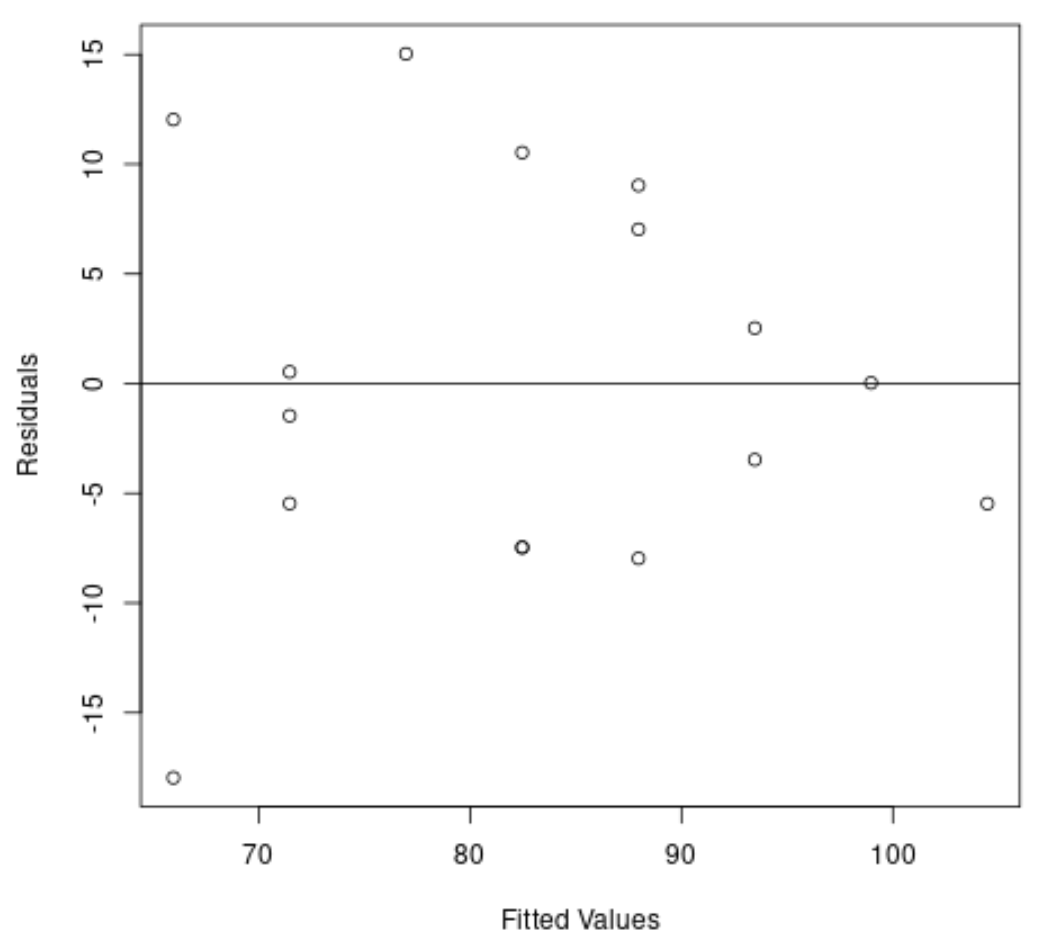
Затем мы создадим график невязок и подобранных значений, чтобы визуально проверить гетероскедастичность:
#create residual vs. fitted plot
plot( fitted (model), resid (model), xlab='Fitted Values', ylab='Residuals')
#add a horizontal line at 0
abline(0,0)
Из графика видно, что остатки имеют форму «конуса» — они не распределены с одинаковой дисперсией по всему графику.
Чтобы формально проверить гетероскедастичность, мы можем выполнить тест Бреуша-Пагана:
#load lmtest package
library (lmtest)
#perform Breusch-Pagan test
bptest(model)
studentized Breusch-Pagan test
data: model
BP = 3.9597, df = 1, p-value = 0.0466
Тест Бреуша-Пагана использует следующие нулевые и альтернативные гипотезы :
- Нулевая гипотеза (H 0 ): присутствует гомоскедастичность (остатки распределены с равной дисперсией)
- Альтернативная гипотеза ( HA ): присутствует гетероскедастичность (остатки не распределены с одинаковой дисперсией)
Поскольку p-значение теста равно 0,0466 , мы отвергаем нулевую гипотезу и делаем вывод, что гетероскедастичность является проблемой в этой модели.
Шаг 4. Выполните взвешенную регрессию методом наименьших квадратов
Поскольку присутствует гетероскедастичность, мы будем выполнять метод взвешенных наименьших квадратов, определяя веса таким образом, чтобы наблюдения с более низкой дисперсией имели больший вес:
#define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2
#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)
#view summary of model
summary(wls_model)
Call:
lm(formula = score ~ hours, data = df, weights = wt)
Weighted Residuals:
Min 1Q Median 3Q Max
-2.0167 -0.9263 -0.2589 0.9873 1.6977
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.9689 5.1587 12.400 6.13e-09 \*\*\*
hours 4.7091 0.8709 5.407 9.24e-05 \*\*\*
---
Signif. codes: 0 ‘\*\*\*’ 0.001 ‘\*\*’ 0.01 ‘\*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05
Из вывода мы видим, что оценка коэффициента для часов переменной предиктора немного изменилась, и общее соответствие модели улучшилось.
Модель взвешенных наименьших квадратов имеет остаточную стандартную ошибку 1,199 по сравнению с 9,224 в исходной модели простой линейной регрессии.
Это указывает на то, что прогнозируемые значения, полученные с помощью взвешенной модели наименьших квадратов, намного ближе к фактическим наблюдениям по сравнению с прогнозируемыми значениями, полученными с помощью простой модели линейной регрессии.
Взвешенная модель наименьших квадратов также имеет R-квадрат 0,6762 по сравнению с 0,6296 в исходной модели простой линейной регрессии.
Это указывает на то, что модель взвешенных наименьших квадратов способна объяснить больше различий в экзаменационных баллах по сравнению с простой моделью линейной регрессии.
Эти метрики показывают, что взвешенная модель наименьших квадратов обеспечивает лучшее соответствие данным по сравнению с простой моделью линейной регрессии.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить квантильную регрессию в R