Модераторная переменная — это тип переменной, который влияет на связь между зависимой и независимой переменными .
При выполнении регрессионного анализа нам часто интересно понять, как изменения независимой переменной влияют на зависимую переменную. Однако иногда на эту взаимосвязь может повлиять модерирующая переменная.
Например, предположим, что мы хотим подобрать регрессионную модель, в которой мы используем независимую переменную количество часов, потраченных на тренировки каждую неделю , для прогнозирования зависимой переменной частоты сердечных сокращений в состоянии покоя .
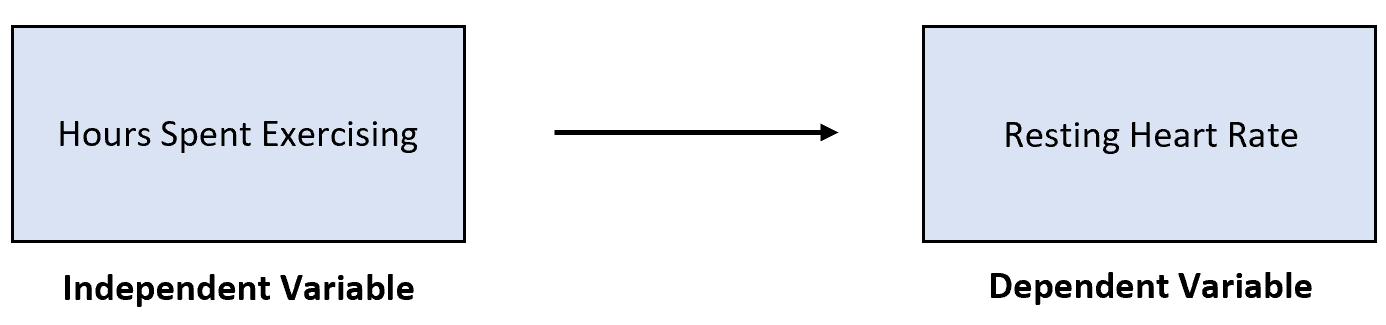
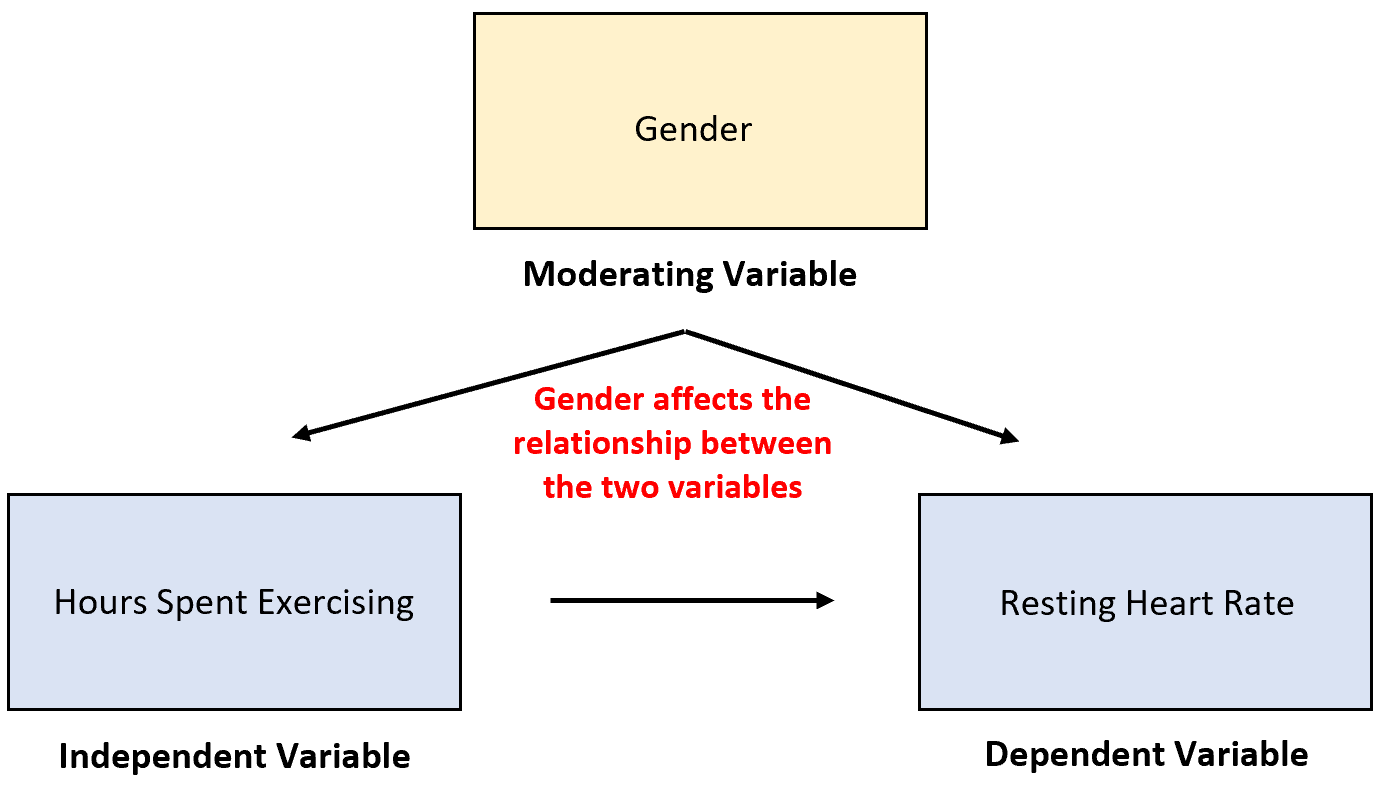
Мы подозреваем, что большее количество часов, проведенных за физическими упражнениями, связано с более низкой частотой сердечных сокращений в состоянии покоя. Однако на эту взаимосвязь может повлиять модерирующая переменная, такая как пол .
Вполне возможно, что каждый дополнительный час упражнений приводит к тому, что частота сердечных сокращений в покое у мужчин падает сильнее, чем у женщин.
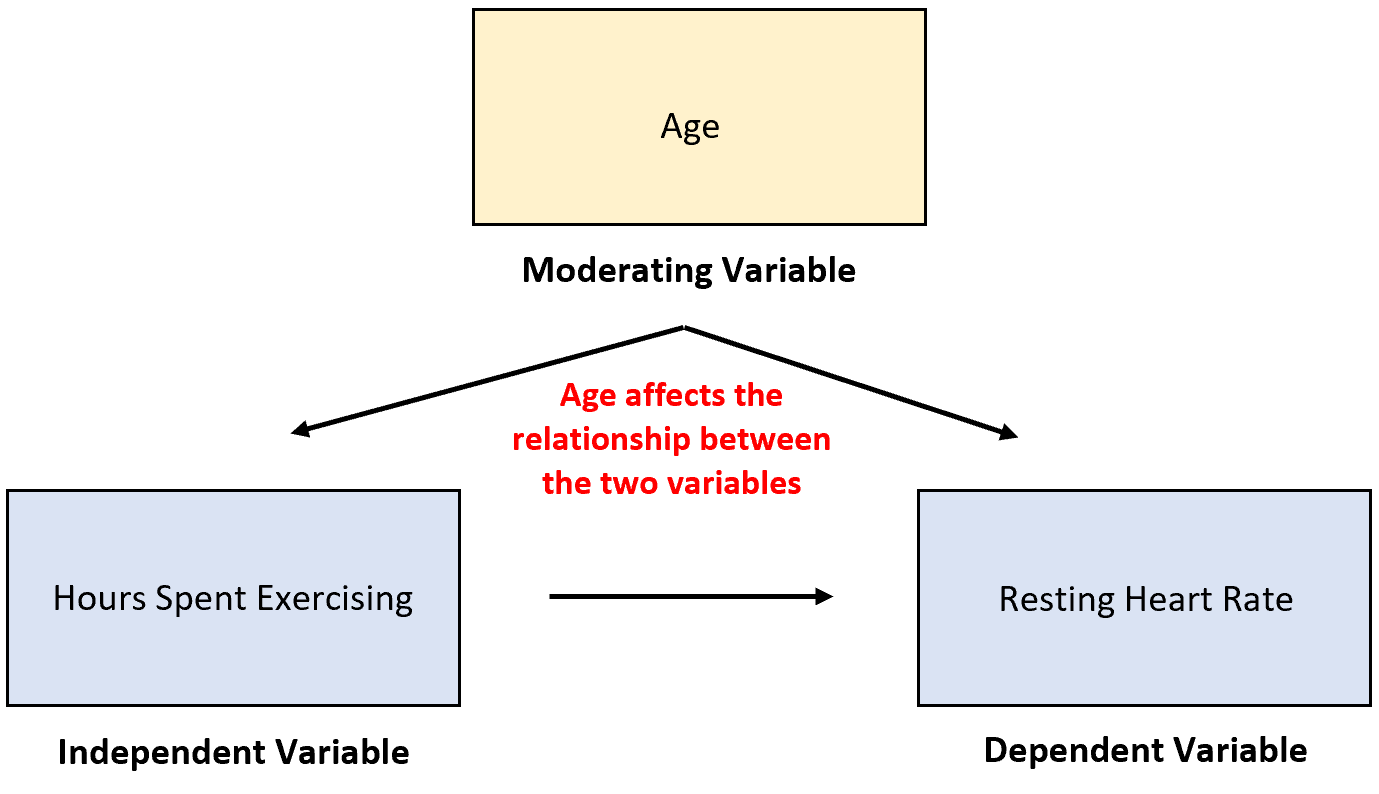
Другим примером модерирующей переменной может быть возраст.Вполне вероятно, что каждый дополнительный час упражнений приводит к тому, что частота сердечных сокращений в покое у молодых людей падает больше, чем у пожилых людей.
Свойства модерирующих переменных
У модерирующих переменных есть следующие свойства:
1. Умеренные переменные могут быть качественными или количественными .
Качественные переменные — это переменные, которые принимают имена или ярлыки. Примеры включают:
- Пол (мужской или женский)
- Уровень образования (степень средней школы, степень бакалавра, степень магистра и т.д.)
- Семейное положение (холост, женат, разведен)
Количественные переменные — это переменные, которые принимают числовые значения. Примеры включают:
- Возраст
- Высота
- Квадратные метры
- Численность населения
В предыдущих примерах пол был качественной переменной, которая могла влиять на взаимосвязь между изучаемыми часами и частотой сердечных сокращений в состоянии покоя, тогда как возраст был количественной переменной, которая потенциально могла влиять на взаимосвязь.
2. Сдерживающие переменные могут по-разному влиять на отношение между независимой и зависимой переменной.
Умеренные переменные могут иметь следующие эффекты:
- Укрепите связь между двумя переменными.
- Ослабьте связь между двумя переменными.
- Отменить связь между двумя переменными.
В зависимости от ситуации модерирующая переменная может смягчить отношения между двумя переменными разными способами.
Как протестировать модерирующие переменные
Если X — независимая переменная (иногда называемая переменной «предиктор»), а Y — зависимая переменная (иногда называемая переменной «отклика»), то мы могли бы написать уравнение регрессии для описания взаимосвязи между двумя переменными следующим образом:
Y = β 0 + β 1 X
Если мы подозреваем, что какая-то другая переменная, Z , является модераторной переменной, то мы могли бы подобрать следующую модель регрессии:
Y = β 0 + β 1 X 1 + β 2 Z+ β 3 XZ
В этом уравнении член XZ известен как член взаимодействия .
Если значение p для коэффициента XZ в выходных данных регрессии является статистически значимым, то это указывает на то, что существует значительное взаимодействие между X и Z , и Z следует включить в регрессионную модель в качестве модерирующей переменной.
Мы запишем окончательную модель как:
Y = β 0 + β 1 X + β 2 Z+ β 3 XZ
Если p-значение для коэффициента XZ в выходных данных регрессии не является статистически значимым, то Z не является модераторной переменной.
Однако возможно, что коэффициент для Z все еще может быть статистически значимым. В этом случае мы бы просто включили Z как еще одну независимую переменную в регрессионную модель.
Затем мы запишем окончательную модель как:
Y = β 0 + β 1 X + β 2 Z
Дополнительные ресурсы
Как читать и интерпретировать таблицу регрессии
Как использовать фиктивные переменные в регрессионном анализе
Введение в смешанные переменные