Когда взаимосвязь между набором переменных-предикторов и переменной отклика очень сложна, мы часто используем нелинейные методы для моделирования взаимосвязи между ними.
Одним из таких методов является построение дерева решений.Однако недостатком использования одного дерева решений является высокая дисперсия.То есть, если мы разделим набор данных на две половины и применим дерево решений к обеим половинам, результаты могут быть совершенно разными.
Один из методов, который мы можем использовать для уменьшения дисперсии одного дерева решений, — построить модель случайного леса , которая работает следующим образом:
1. Возьмите b образцов с начальной загрузкой из исходного набора данных.
2. Постройте дерево решений для каждого загруженного образца.
- При построении дерева каждый раз, когда рассматривается разделение, только случайная выборка из m предикторов рассматривается как кандидаты на разделение из полного набора p предикторов. Обычно мы выбираем m равным √ p .
3. Усредните прогнозы каждого дерева, чтобы получить окончательную модель.
Оказывается, случайные леса, как правило, создают гораздо более точные модели по сравнению с одиночными деревьями решений и даже моделями с пакетами.
В этом руководстве представлен пошаговый пример создания модели случайного леса для набора данных в R.
Шаг 1: Загрузите необходимые пакеты
Сначала мы загрузим необходимые пакеты для этого примера. Для этого простого примера нам нужен только один пакет:
library (randomForest)
Шаг 2: Подберите модель случайного леса
В этом примере мы будем использовать встроенный набор данных R под названием airquality , который содержит измерения качества воздуха в Нью-Йорке за 153 отдельных дня.
#view structure of airquality dataset
str(airquality)
'data.frame': 153 obs. of 6 variables:
$ Ozone : int 41 36 12 18 NA 28 23 19 8 NA ...
$ Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
$ Wind : num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
$ Temp : int 67 72 74 62 56 66 65 59 61 69 ...
$ Month : int 5 5 5 5 5 5 5 5 5 5 ...
$ Day : int 1 2 3 4 5 6 7 8 9 10 ...
#find number of rows with missing values
sum(! complete.cases (airquality))
[1] 42
Этот набор данных имеет 42 строки с пропущенными значениями, поэтому, прежде чем мы подберем модель случайного леса, мы заполним пропущенные значения в каждом столбце медианами столбцов:
#replace NAs with column medians
for (i in 1: ncol (airquality)) {
airquality[ , i][ is.na (airquality[ , i])] <- median (airquality[ , i], na.rm = TRUE )
}
Связанный: Как вменить пропущенные значения в R
В следующем коде показано, как подобрать модель случайного леса в R с помощью функции randomForest() из пакета randomForest .
#make this example reproducible
set.seed(1)
#fit the random forest model
model <- randomForest(
formula = Ozone ~ .,
data = airquality
)
#display fitted model
model
Call:
randomForest(formula = Ozone ~ ., data = airquality)
Type of random forest: regression
Number of trees: 500
No. of variables tried at each split: 1
Mean of squared residuals: 327.0914
% Var explained: 61
#find number of trees that produce lowest test MSE
which.min(model$mse)
[1] 82
#find RMSE of best model
sqrt(model$mse[ which.min (model$mse)])
[1] 17.64392
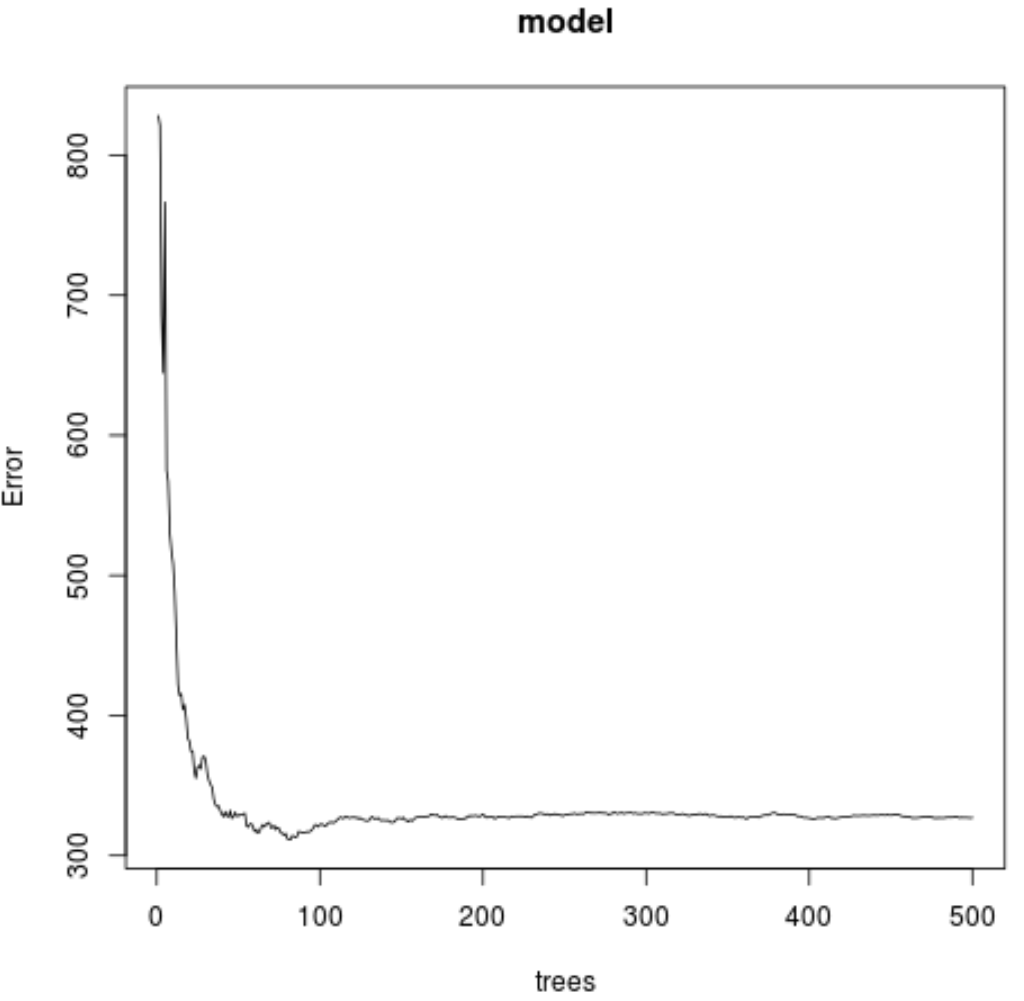
Из вывода видно, что модель, давшая наименьшую среднеквадратичную ошибку теста (MSE), использовала 82 дерева.
Мы также можем видеть, что среднеквадратическая ошибка этой модели составила 17,64392.Мы можем думать об этом как о средней разнице между прогнозируемым значением озона и фактическим наблюдаемым значением.
Мы также можем использовать следующий код для создания графика тестовой MSE на основе количества используемых деревьев:
#plot the test MSE by number of trees
plot(model)
И мы можем использовать функцию varImpPlot() для создания графика, отображающего важность каждой переменной-предиктора в окончательной модели:
#produce variable importance plot
varImpPlot(model)
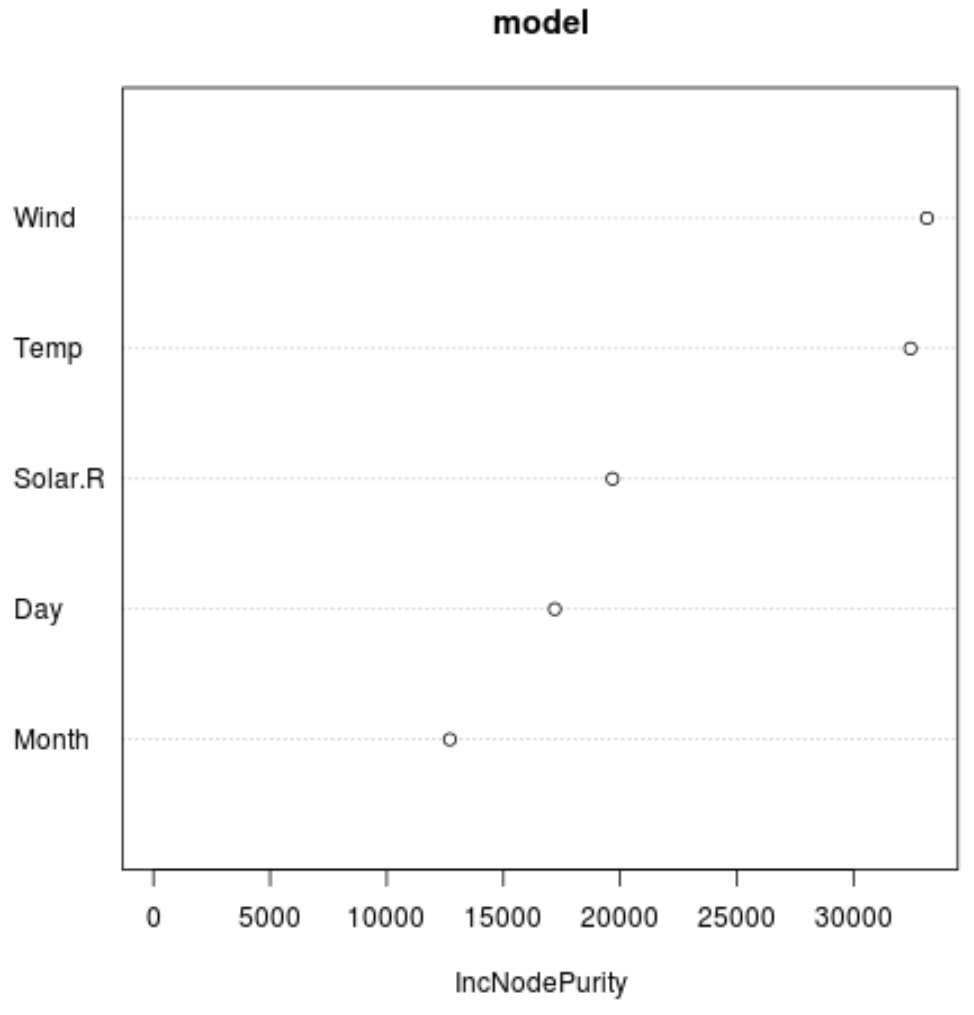
По оси X отображается среднее увеличение чистоты узлов деревьев регрессии на основе разделения по различным предикторам, отображаемым по оси Y.
Из графика видно, что Wind является самой важной предикторной переменной, за которой следует Temp .
Шаг 3: Настройте модель
По умолчанию функция randomForest() использует 500 деревьев и (всего предикторов/3) случайно выбранных предикторов в качестве потенциальных кандидатов при каждом разбиении. Мы можем настроить эти параметры с помощью функции tuneRF() .
Следующий код показывает, как найти оптимальную модель, используя следующие спецификации:
- ntreeTry: количество деревьев, которые необходимо построить.
- mtryStart: начальное количество переменных-предикторов, которые следует учитывать при каждом разбиении.
- stepFactor: коэффициент, на который следует увеличивать до тех пор, пока оценочная ошибка вне упаковки не перестанет улучшаться на определенную величину.
- улучшить: Величина, на которую необходимо улучшить ошибку вне упаковки, чтобы продолжать увеличивать ступенчатый коэффициент.
model_tuned <- tuneRF(
x=airquality[,-1], #define predictor variables
y=airquality$Ozone, #define response variable
ntreeTry= 500 ,
mtryStart= 4 ,
stepFactor= 1.5 ,
improve= 0.01 ,
trace= FALSE #don't show real-time progress
)
Эта функция создает следующий график, который отображает количество предикторов, используемых в каждом разбиении при построении деревьев по оси x и оценочную ошибку вне пакета по оси y:
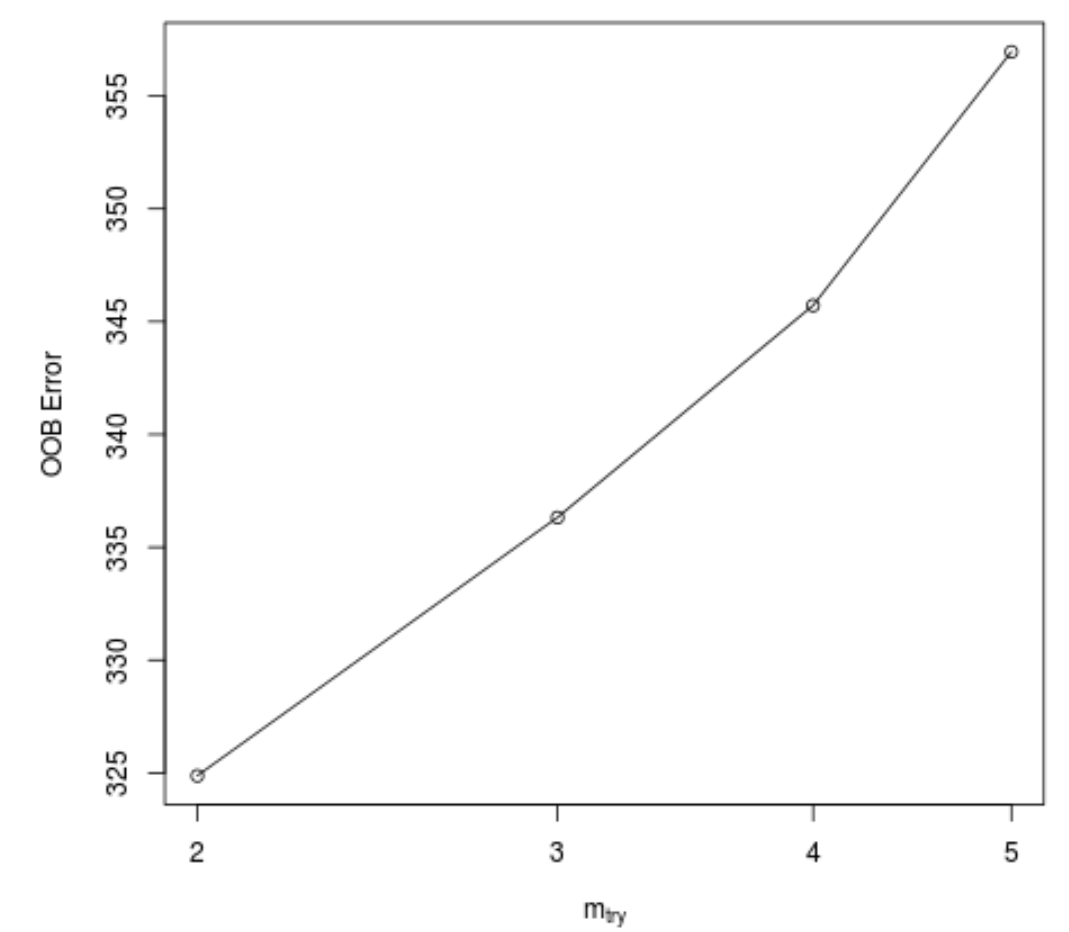
Мы видим, что наименьшая ошибка OOB достигается за счет использования 2 случайно выбранных предикторов в каждом разбиении при построении деревьев.
Фактически это соответствует параметру по умолчанию (всего предикторов/3 = 6/3 = 2), используемому исходной функцией randomForest() .
Шаг 4: Используйте окончательную модель для прогнозирования
Наконец, мы можем использовать подобранную модель случайного леса, чтобы делать прогнозы на основе новых наблюдений.
#define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)
#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)
27.19442
Основываясь на значениях переменных-предикторов, подобранная модель случайного леса предсказывает, что значение озона будет 27,19442 в этот конкретный день.
Полный код R, использованный в этом примере, можно найти здесь .