Повторные измерения ANOVA используются для определения того, существует ли статистически значимая разница между средними значениями трех или более групп, в которых одни и те же субъекты обнаруживаются в каждой группе.
ANOVA с повторными измерениями обычно используется в двух конкретных ситуациях:
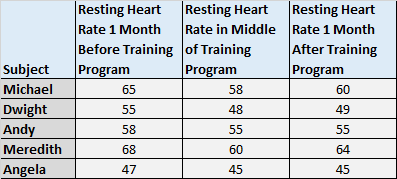
1. Измерение средних баллов испытуемых в течение трех или более моментов времени. Например, вы можете захотеть измерить частоту сердечных сокращений в покое у испытуемых за месяц до начала тренировочной программы, в середине тренировочной программы и через месяц после тренировочной программы, чтобы увидеть, есть ли существенная разница в среднем значении пульса в состоянии покоя. скорость через эти три момента времени.
Обратите внимание, как одни и те же предметы появляются в каждый момент времени. Мы неоднократно измеряли одних и тех же субъектов, поэтому мы использовали повторные измерения ANOVA.
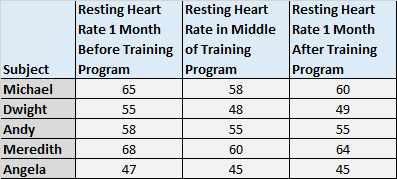
2. Измерение средних баллов испытуемых в трех разных условиях. Например, вы можете попросить испытуемых посмотреть три разных фильма и оценить каждый из них в зависимости от того, насколько он им понравился.
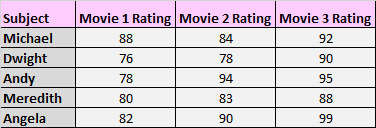
Опять же, в каждой группе появляются одни и те же субъекты, поэтому нам нужно использовать дисперсионный анализ с повторными измерениями, чтобы проверить разницу в средних значениях для этих трех условий.
Однофакторный дисперсионный анализ в сравнении с повторными измерениями дисперсионного анализа
В типичном однофакторном ANOVA в каждой группе используются разные предметы. Например, мы можем попросить субъектов оценить три фильма, как в приведенном выше примере, но мы используем разные предметы для оценки каждого фильма:
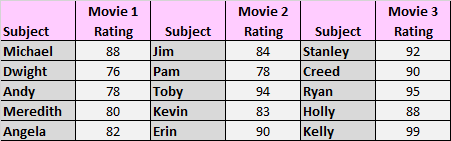
В этом случае мы проведем типичный односторонний дисперсионный анализ, чтобы проверить разницу между средними оценками трех фильмов.
В реальной жизни есть два преимущества использования одних и тех же субъектов при различных условиях лечения:
1. Исследователям дешевле и быстрее набирать и платить меньшему количеству людей для проведения эксперимента, поскольку они могут просто получать данные от одних и тех же людей несколько раз.
2. Мы можем приписать некоторую дисперсию данных самим испытуемым, что облегчает получение меньшего p-значения.
Один потенциальный недостаток этого типа дизайна заключается в том, что испытуемые могут устать или устать, если эксперимент длится слишком долго, что может исказить результаты. Например, испытуемые могут дать более низкую оценку третьему фильму, который они смотрят, потому что они устали и готовы идти домой.
Повторные измерения ANOVA: пример
Предположим, мы набираем пять испытуемых для участия в программе обучения. Мы измеряем их частоту сердечных сокращений в состоянии покоя до участия в тренировочной программе, после участия в течение 4 месяцев и после участия в течение 8 месяцев.
В следующей таблице показаны результаты:
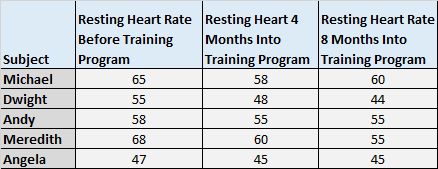
Мы хотим знать, есть ли разница в средней частоте сердечных сокращений в покое в эти три временных момента, поэтому мы проводим повторный анализ ANOVA на уровне значимости 0,05, используя следующие шаги:
Шаг 1. Сформулируйте гипотезы.
Нулевая гипотеза (H 0 ): µ 1 = µ 2 = µ 3 (все средние значения населения равны)
Альтернативная гипотеза: (Ha): по крайней мере одно среднее значение генеральной совокупности отличается от остальных
Шаг 2. Выполните повторные измерения ANOVA.
Мы будем использовать калькулятор повторных измерений ANOVA со следующими входными данными:
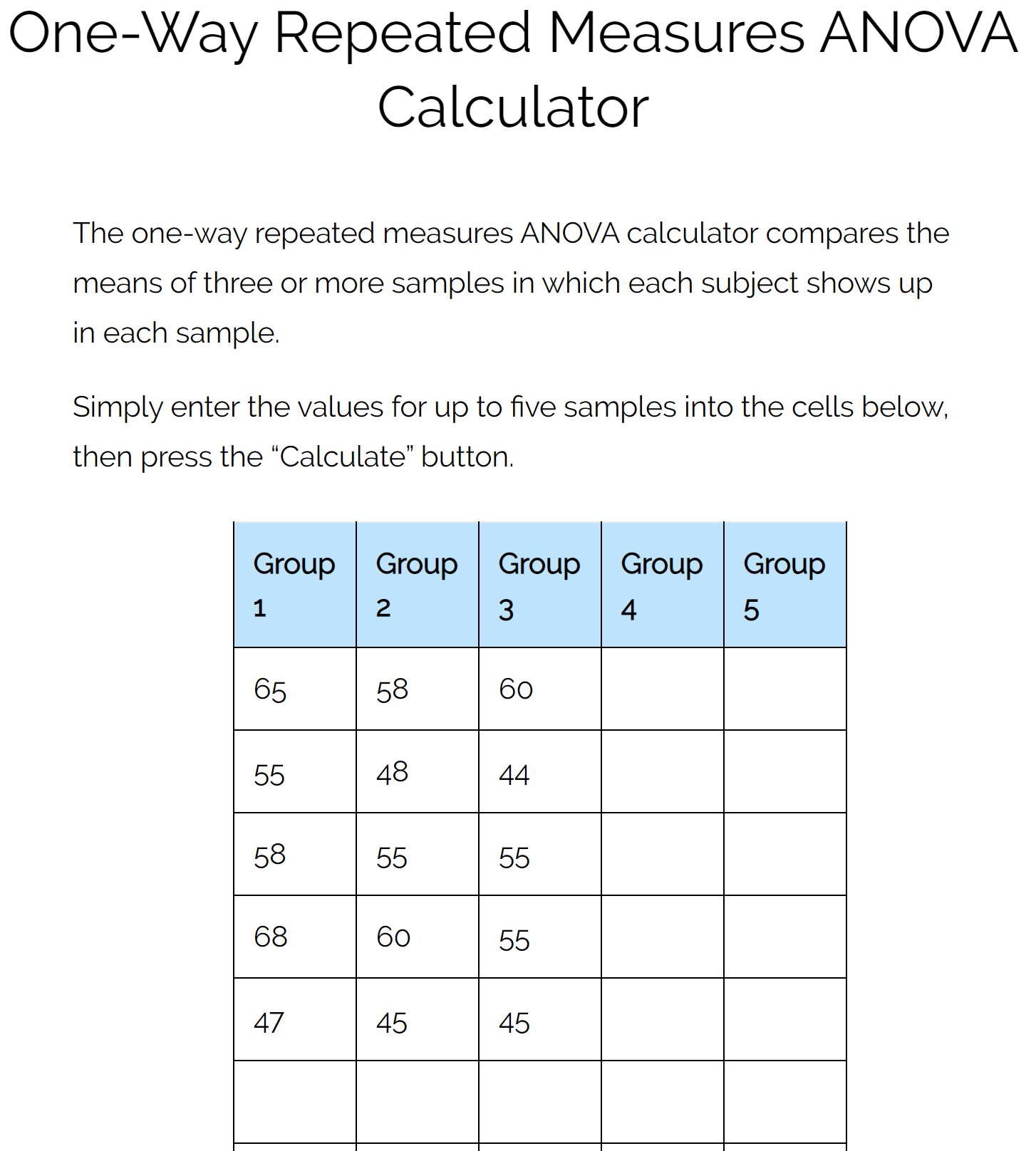
Как только мы нажмем «Рассчитать», автоматически появится следующий вывод:
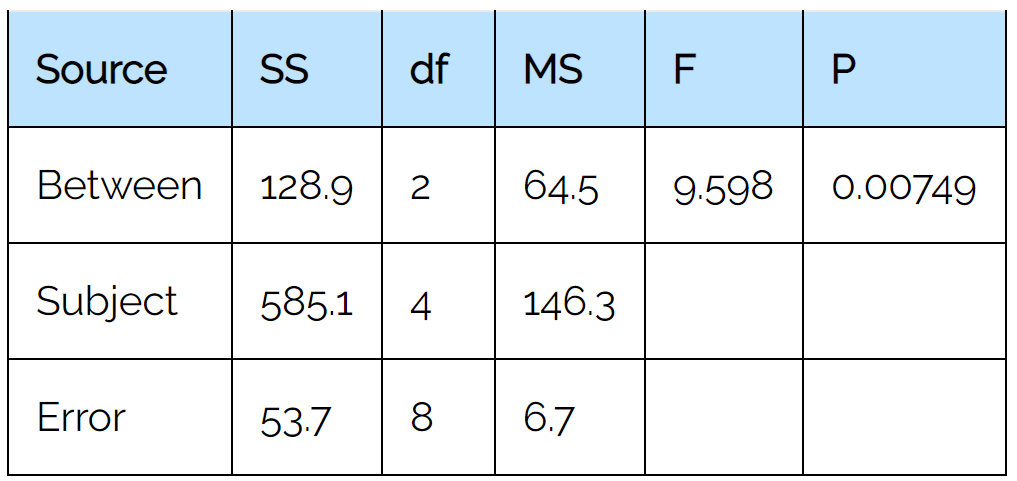
Шаг 3. Интерпретируйте результаты.
Из выходной таблицы мы видим, что статистика F-теста равна 9,598 , а соответствующее значение p равно 0,00749 .
Поскольку это p-значение меньше 0,05, мы отвергаем нулевую гипотезу. Это означает, что у нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средней частотой сердечных сокращений в состоянии покоя в три разных момента времени.
Дополнительные ресурсы
В следующих статьях объясняется, как выполнять повторные измерения ANOVA с использованием различных статистических программ:
Повторные измерения ANOVA в Excel
Повторные измерения ANOVA в R
Повторные измерения ANOVA в Stata
Повторные измерения ANOVA в Python
Повторные измерения ANOVA в SPSS
Повторные измерения ANOVA в Google Sheets
Повторные измерения ANOVA вручную
Калькулятор повторных измерений ANOVA