Статистическая гипотеза – это предположение о параметре совокупности.Например, мы можем предположить, что средний рост мужчины в США составляет 70 дюймов. Предположение о росте является статистической гипотезой , а истинный средний рост мужчины в США является популяционным параметром .
Тест гипотезы — это формальный статистический тест, который мы используем, чтобы отвергнуть или не отвергнуть некоторую статистическую гипотезу.
Основной процесс проверки гипотезы выглядит следующим образом:
1. Соберите образцы данных.
2. Рассчитайте статистику стандартизированного теста для выборочных данных.
3. Сравните статистику стандартизированного теста с некоторым критическим значением. Если оно более экстремально, чем критическое значение, отклоните нулевую гипотезу. В противном случае не удастся отклонить проверку нулевой гипотезы.
Формула, которую мы используем для расчета статистики стандартизированного теста, зависит от типа проверки гипотезы, которую мы проводим.
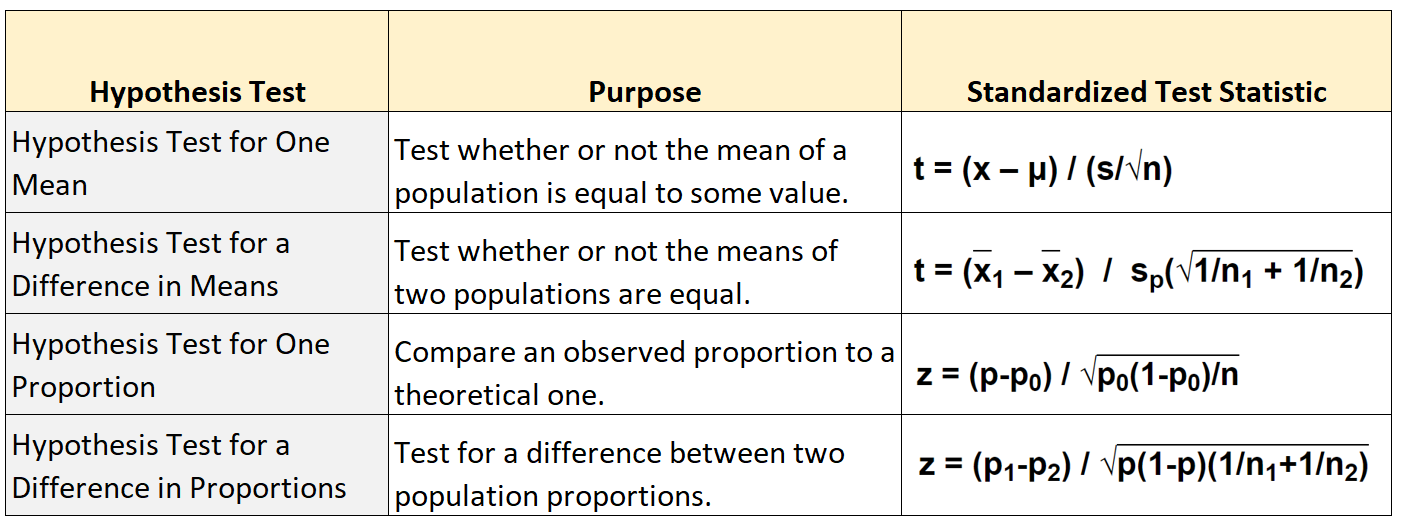
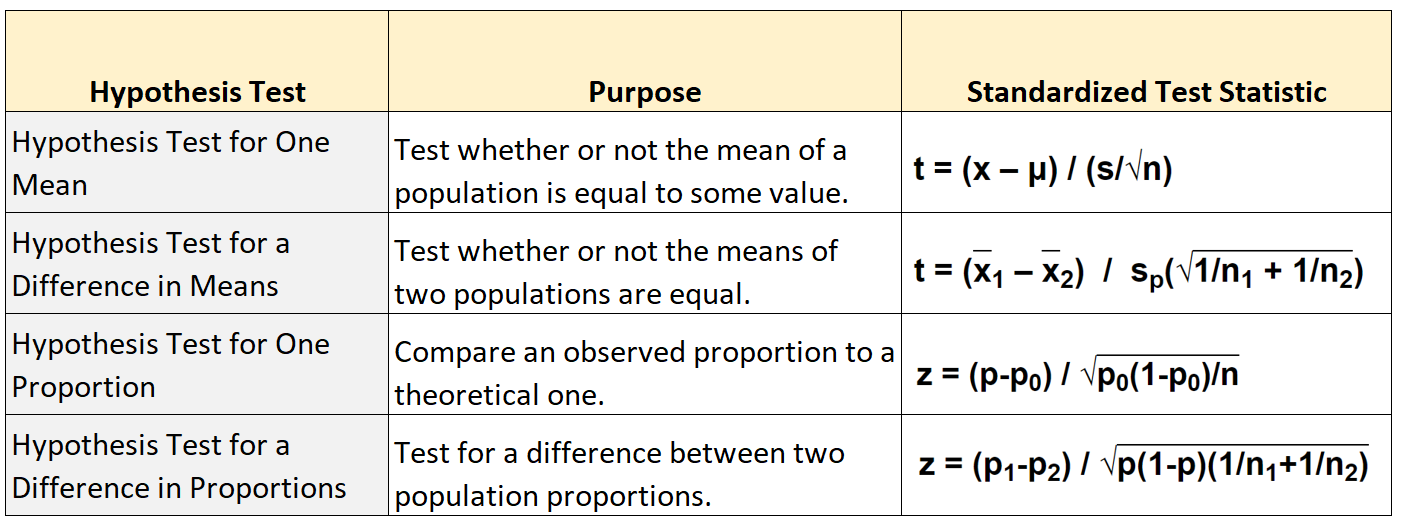
В следующей таблице показана формула, используемая для расчета статистики стандартизированного теста для каждого из четырех основных типов проверки гипотез:
Тест гипотезы для одного среднего
Одновыборочный t-критерий используется для проверки того, равно ли среднее значение совокупности некоторому значению.
Стандартизированная статистика теста для этого типа теста рассчитывается следующим образом:
т = ( х - μ) / (с / √n)
куда:
- x: выборочное среднее
- μ 0 : предполагаемое среднее значение населения
- s: стандартное отклонение выборки
- n: размер выборки
Обратитесь к этому учебнику за примером того, как рассчитать эту стандартизированную тестовую статистику.
Проверка гипотезы о разнице в средствах
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.
Стандартизированная статистика теста для этого типа теста рассчитывается следующим образом:
т знак равно ( Икс 1 - Икс 2 ) / s п (√ 1 / п 1 + 1 / п 2 )
где x 1 и x 2 — средние значения выборки, n 1 и n 2 — размеры выборки, и где s p рассчитывается как:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
где s 1 2 и s 2 2 — выборочные дисперсии.
Обратитесь к этому учебнику за примером того, как рассчитать эту стандартизированную тестовую статистику.
Проверка гипотезы для одной пропорции
Z-критерий одной пропорции используется для сравнения наблюдаемой пропорции с теоретической.
Стандартизированная статистика теста для этого типа теста рассчитывается следующим образом:
z = (pp 0 ) / √ p 0 (1-p 0 )/n
куда:
- p: наблюдаемая доля выборки
- p 0 : предполагаемая доля населения
- n: размер выборки
Обратитесь к этому учебнику за примером того, как рассчитать эту стандартизированную тестовую статистику.
Проверка гипотезы о разнице в пропорциях
Z-критерий двух пропорций используется для проверки разницы между двумя пропорциями населения.
Стандартизированная статистика теста для этого типа теста рассчитывается следующим образом:
*z* = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
где p 1 и p 2 — пропорции выборки, n 1 и n 2 — размеры выборки, и где p — общая объединенная доля, рассчитанная как:
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
Обратитесь к этому учебнику за примером того, как рассчитать эту стандартизированную тестовую статистику.