В обычной множественной линейной регрессии мы используем набор переменных предикторов p и переменную отклика, чтобы соответствовать модели формы:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p X p + ε
Значения β 0 , β 1 , B 2 , … , β p выбираются методом наименьших квадратов, который минимизирует сумму квадратов невязок (RSS):
RSS = Σ(y i – ŷ i ) 2
куда:
- Σ : символ, означающий «сумма».
- y i : Фактическое значение отклика для i -го наблюдения
- ŷ i : прогнозируемое значение отклика для i -го наблюдения.
Проблема мультиколлинеарности в регрессии
Одной из проблем, которая часто возникает на практике с множественной линейной регрессией, является мультиколлинеарность , когда две или более переменных-предикторов сильно коррелируют друг с другом, так что они не предоставляют уникальную или независимую информацию в регрессионной модели.
Это может привести к тому, что оценки коэффициентов модели будут ненадежными и будут иметь высокую дисперсию. То есть, когда модель применяется к новому набору данных, которого она раньше не видела, она, скорее всего, будет работать плохо.
Как избежать мультиколлинеарности: регрессия гребня и лассо
Два метода, которые мы можем использовать, чтобы обойти эту проблему мультиколлинеарности, — это гребневая регрессия и лассо-регрессия .
Гребневая регрессия направлена на минимизацию следующего:
- RSS + λΣβ j 2
Регрессия Лассо стремится минимизировать следующее:
- RSS + λΣ|β j |
В обоих уравнениях второй член известен как штраф за усадку .
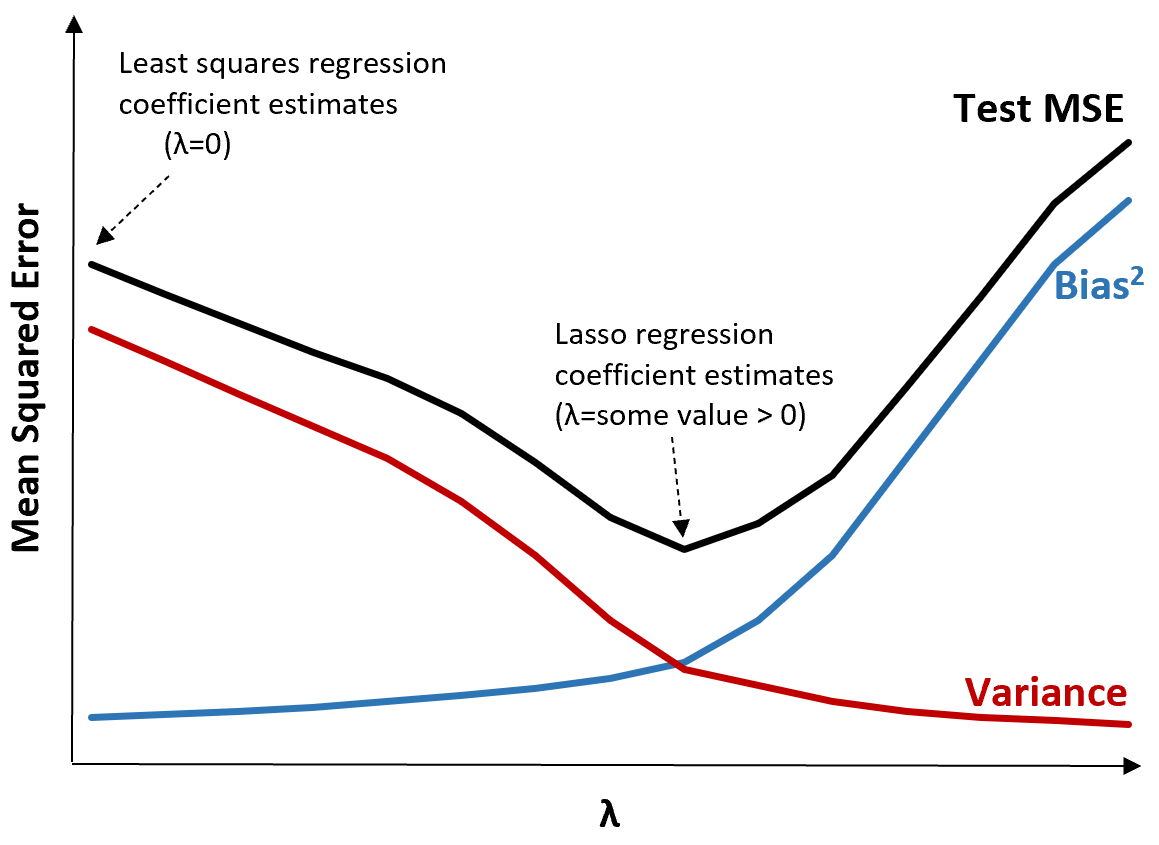
Когда λ = 0, этот штрафной член не имеет эффекта, и как регрессия гребня, так и регрессия лассо дают те же оценки коэффициентов, что и метод наименьших квадратов.
Однако по мере того, как λ приближается к бесконечности, штраф за сжатие становится более влиятельным, и переменные-предикторы, которые нельзя импортировать в модель, сжимаются до нуля.
При регрессии Лассо возможно, что некоторые коэффициенты могут полностью обнулиться, когда λ становится достаточно большим.
Плюсы и минусы ридж- и лассо-регрессии
Преимущество регрессии гребня и лассо по сравнению с регрессией методом наименьших квадратов заключается в компромиссе смещения и дисперсии .
Напомним, что среднеквадратическая ошибка (MSE) — это показатель, который мы можем использовать для измерения точности данной модели, и он рассчитывается как:
MSE = Var( f̂( x0)) + [Bias( f̂( x0))] 2 + Var(ε)
MSE = дисперсия + погрешность 2 + неустранимая ошибка
Основная идея как регрессии гребня, так и регрессии лассо состоит в том, чтобы ввести небольшое смещение, чтобы можно было существенно уменьшить дисперсию, что приводит к более низкому общему значению MSE.
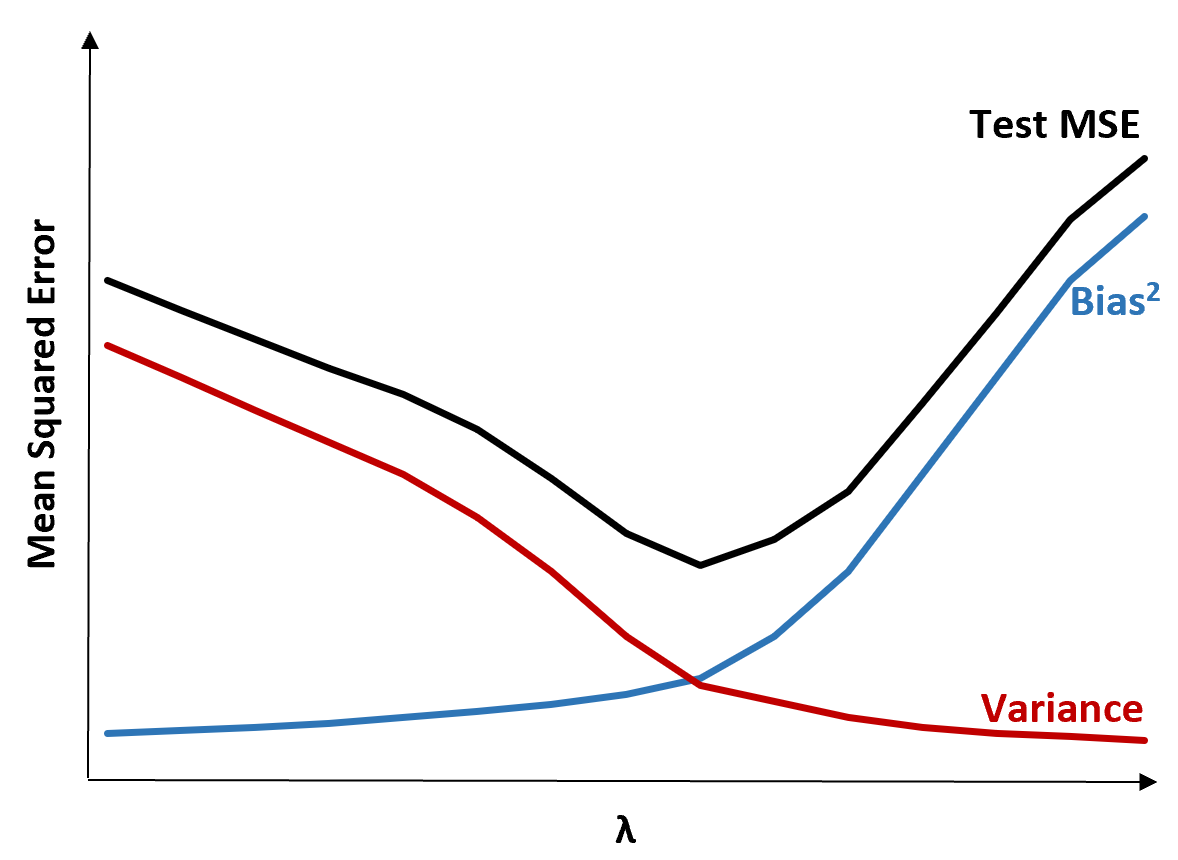
Чтобы проиллюстрировать это, рассмотрим следующую диаграмму:
Обратите внимание, что по мере увеличения λ дисперсия существенно падает с очень небольшим увеличением смещения. Однако после определенного момента дисперсия уменьшается менее быстро, а сокращение коэффициентов приводит к их значительному недооцениванию, что приводит к значительному увеличению систематической ошибки.
Из диаграммы видно, что тестовая MSE является самой низкой, когда мы выбираем значение для λ, которое обеспечивает оптимальный компромисс между смещением и дисперсией.
Когда λ = 0, штрафной член в регрессии лассо не имеет эффекта и, таким образом, дает те же оценки коэффициентов, что и метод наименьших квадратов. Однако, увеличивая λ до определенной точки, мы можем уменьшить общую тестовую MSE.
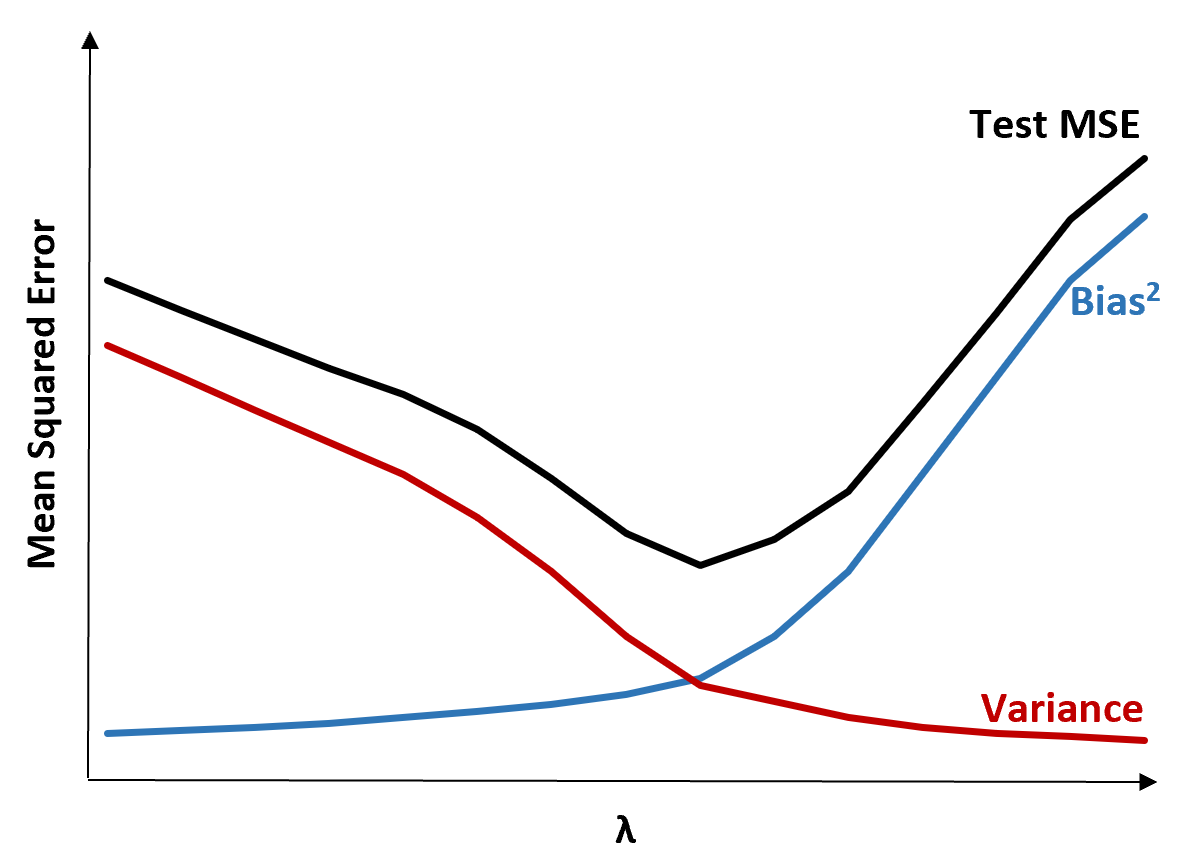
Это означает, что модель, подобранная с помощью регрессии гребня и лассо, может потенциально давать меньшие ошибки тестирования, чем модель, подобранная с помощью регрессии наименьших квадратов.
Недостаток регрессии гребня и лассо заключается в том, что становится трудно интерпретировать коэффициенты в окончательной модели, поскольку они сжимаются до нуля.
Таким образом, гребенчатую регрессию и регрессию лассо следует использовать, когда вы заинтересованы в оптимизации для прогнозирующей способности, а не для логического вывода.
Ридж против регрессии Лассо: когда использовать каждый
И л -ассо-регрессия, и гребенчатая регрессия известны как методы регуляризации, потому что они оба пытаются минимизировать сумму квадратов остатков (RSS) вместе с некоторым штрафным членом.
Другими словами, они ограничивают или упорядочивают оценки коэффициентов модели.
Это естественно поднимает вопрос: лучше ли регрессия гребня или лассо?
В случаях, когда значимым является лишь небольшое количество переменных-предикторов, регрессия лассо имеет тенденцию работать лучше, потому что она способна полностью сжать незначимые переменные до нуля и удалить их из модели.
Однако, когда в модели значимы многие переменные-предикторы и их коэффициенты примерно равны, гребневая регрессия имеет тенденцию работать лучше, поскольку она сохраняет все предикторы в модели.
Чтобы определить, какая модель лучше делает прогнозы, мы обычно выполняем k-кратную перекрестную проверку и выбираем ту модель, которая дает наименьшую среднеквадратичную ошибку теста.
Дополнительные ресурсы
Следующие учебные пособия представляют собой введение в регрессию Ridge и Lasso:
В следующих руководствах объясняется, как выполнить оба типа регрессии в R и Python: