Множественная линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между двумя или более переменными-предикторами и переменной- откликом .
В этом руководстве объясняется, как выполнить множественную линейную регрессию в SAS.
Шаг 1: Создайте данные
Предположим, мы хотим подобрать модель множественной линейной регрессии, которая использует количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов, чтобы предсказать окончательный балл студентов за экзамен:
Оценка за экзамен = β 0 + β 1 (часы) + β 2 (подготовительные экзамены)
Во-первых, мы будем использовать следующий код для создания набора данных, содержащего эту информацию для 20 студентов:
/\*create dataset\*/
data exam_data;
input hours prep_exams score;
datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;
Шаг 2: выполните множественную линейную регрессию
Далее мы будем использовать proc reg для подбора модели множественной линейной регрессии к данным:
/\*fit multiple linear regression model\*/
proc reg data =exam_data;
model score = hours prep_exams;
run ;
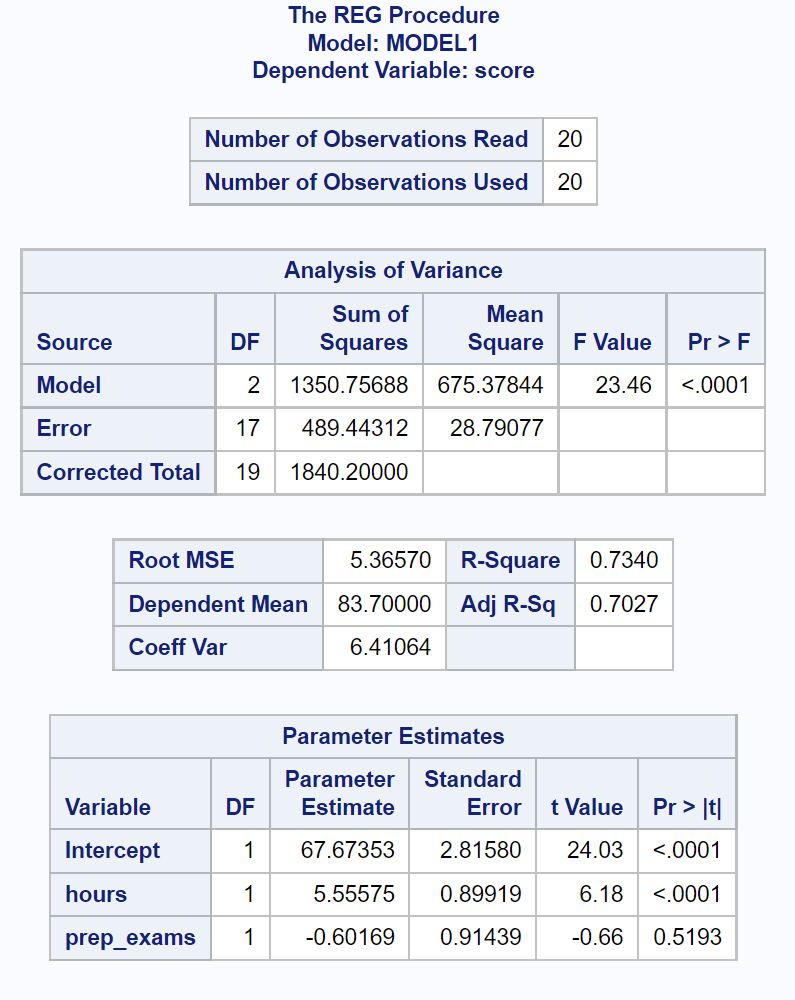
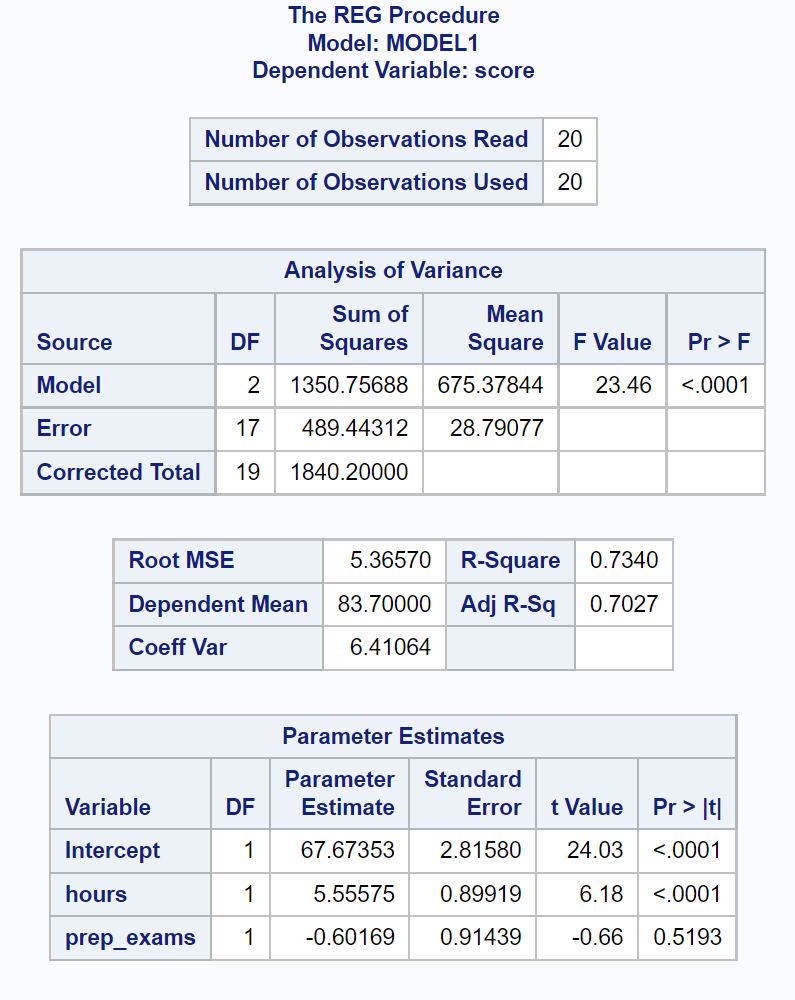
Вот как интерпретировать наиболее релевантные числа в каждой таблице:
Таблица анализа дисперсии:
Общее F-значение регрессионной модели равно 23,46 , а соответствующее p-значение <0,0001 .
Поскольку это p-значение меньше 0,05, мы заключаем, что регрессионная модель в целом является статистически значимой.
Таблица соответствия модели:
Значение R-Square говорит нам о процентной вариации экзаменационных баллов, которую можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
В общем, чем больше значение R-квадрата регрессионной модели, тем лучше переменные-предикторы способны предсказать значение переменной отклика.
В этом случае 73,4% различий в экзаменационных баллах можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Значение Root MSE также полезно знать. Это представляет собой среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии.
В этой регрессионной модели наблюдаемые значения отклоняются от линии регрессии в среднем на 5,3657 единиц.
Таблица оценок параметров:
Мы можем использовать оценочные значения параметров в этой таблице, чтобы написать подобранное уравнение регрессии:
Экзаменационный балл = 67,674 + 5,556*(часы) – 0,602*(подготовительные_экзамены)
Мы можем использовать это уравнение, чтобы найти приблизительную оценку экзамена для учащегося на основе количества часов, которые он проучился, и количества сданных им подготовительных экзаменов.
Например, студент, который занимается 3 часа и сдает 2 подготовительных экзамена, должен получить экзаменационный балл 83,1 :
Расчетный балл за экзамен = 67,674 + 5,556*(3) – 0,602*(2) = 83,1 .
Значение p для часов (<0,0001) меньше 0,05, что означает, что оно имеет статистически значимую связь с экзаменационной оценкой.
Однако значение p для подготовительных экзаменов (0,5193) не меньше 0,05, что означает, что оно не имеет статистически значимой связи с экзаменационным баллом.
Мы можем решить удалить подготовительные экзамены из модели, поскольку они не являются статистически значимыми, и вместо этого выполнитьпростую линейную регрессию , используя часы обучения в качестве единственной переменной-предиктора.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в SAS:
Как рассчитать корреляцию в SAS
Как выполнить простую линейную регрессию в SAS
Как выполнить односторонний ANOVA в SAS