Однофакторный дисперсионный анализ используется для определения наличия статистически значимой разницы между средним значением трех или более независимых групп.
Однофакторный дисперсионный анализ использует следующие нулевую и альтернативную гипотезы:
- H 0 : μ 1 = μ 2 = μ 3 = … = μ k (все групповые средние равны)
- H A : по крайней мере одно среднее значение группы отличаетсяот остальных
Чтобы решить, должны ли мы отклонить или не отклонить нулевую гипотезу, мы должны обратиться к p-значению в выходных данных таблицы ANOVA.
Если p-значение меньше некоторого уровня значимости (например, 0,05), мы можем отклонить нулевую гипотезу и сделать вывод, что не все средние группы равны.
Двухфакторный дисперсионный анализ используется для определения того, существует ли статистически значимое различие между средними значениями трех или более независимых групп, разделенных на две переменные (иногда называемые «факторами»).
Двухфакторный дисперсионный анализ одновременно проверяет три нулевые гипотезы:
- Все групповые средние равны на каждом уровне первой переменной.
- Все групповые средние равны на каждом уровне второй переменной.
- Нет эффекта взаимодействия между двумя переменными
Чтобы решить, должны ли мы отклонить или не отклонить каждую нулевую гипотезу, мы должны обратиться к p-значениям в выходных данных таблицы двустороннего дисперсионного анализа.
В следующих примерах показано, как принять решение об отклонении или отклонении нулевой гипотезы как в однофакторном, так и в двухфакторном дисперсионном анализе.
Пример 1: Однофакторный дисперсионный анализ
Предположим, мы хотим знать, приводят ли три разные программы подготовки к экзаменам к разным средним баллам на определенном экзамене. Чтобы проверить это, мы набираем 30 студентов для участия в исследовании и разделяем их на три группы.
Студенты в каждой группе случайным образом назначаются для использования одной из трех программ подготовки к экзамену в течение следующих трех недель для подготовки к экзамену. По истечении трех недель все студенты сдают один и тот же экзамен.
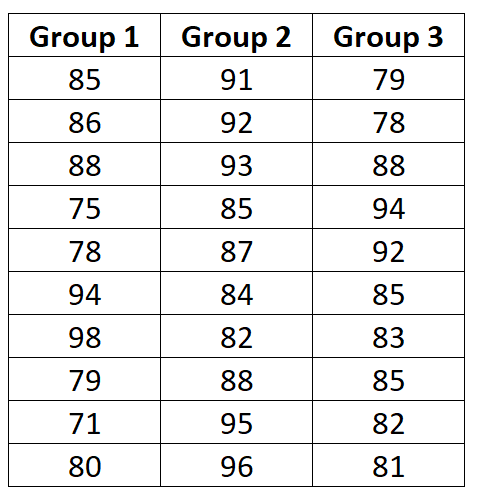
Ниже представлены результаты экзаменов для каждой группы:
Когда мы вводим эти значения в калькулятор однофакторного дисперсионного анализа , мы получаем на выходе следующую таблицу дисперсионного анализа:
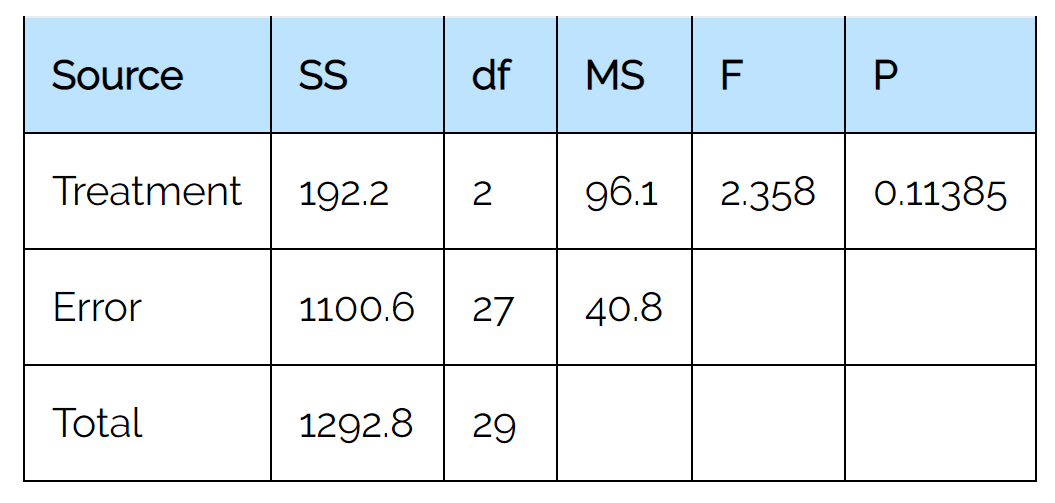
Обратите внимание, что p-значение равно 0,11385 .
Для этого конкретного примера мы будем использовать следующие нулевые и альтернативные гипотезы:
- H 0 : μ 1 = μ 2 = μ 3 (средний балл экзамена для каждой группы равен)
- H A : по крайней мере одно среднее значение группы отличаетсяот остальных
Поскольку p-значение из таблицы ANOVA не меньше 0,05, мы не можем отклонить нулевую гипотезу.
Это означает, что у нас нет достаточных доказательств, чтобы сказать, что существует статистически значимая разница между средними экзаменационными баллами трех групп.
Пример 2: Двухфакторный дисперсионный анализ
Предположим, ботаник хочет знать, влияет ли на рост растений воздействие солнечного света и частота полива.
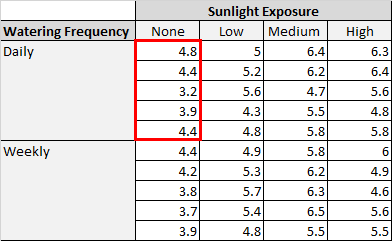
Она сажает 40 семян и дает им расти в течение двух месяцев при различных условиях солнечного света и частоты полива. Через два месяца она записывает высоту каждого растения. Результаты показаны ниже:
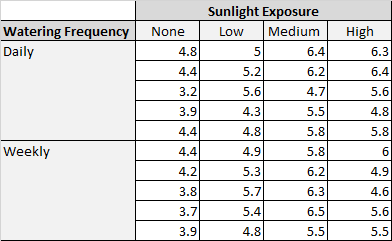
В таблице выше мы видим, что в каждой комбинации условий выращивалось по пять растений.
Например, было пять растений, выращенных с ежедневным поливом и без солнечного света, и их высота через два месяца составила 4,8 дюйма, 4,4 дюйма, 3,2 дюйма, 3,9 дюйма и 4,4 дюйма:
Она выполняет двусторонний ANOVA в Excel и получает следующий результат:
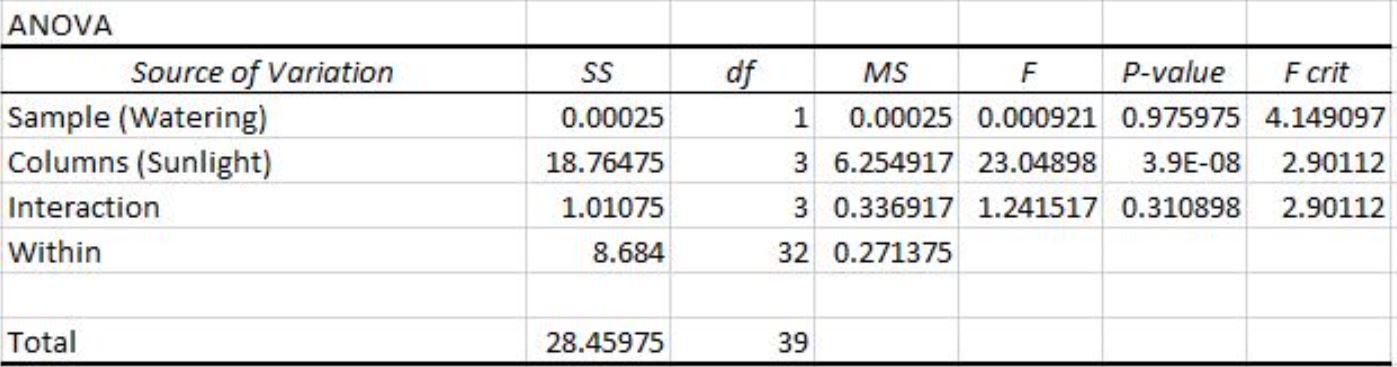
Мы можем видеть следующие p-значения в выходных данных таблицы двустороннего ANOVA:
- Значение p для частоты полива составляет 0,975975.Это не является статистически значимым при уровне значимости 0,05.
- Значение p для воздействия солнечного света составляет 3,9E-8 (0,000000039).Это статистически значимо при уровне значимости 0,05.
- Значение p для взаимодействия между частотой полива и воздействием солнечного света составляет 0,310898.Это не является статистически значимым при уровне значимости 0,05.
Эти результаты показывают, что воздействие солнечного света является единственным фактором, статистически значимо влияющим на высоту растений.
А поскольку эффекта взаимодействия нет, эффект воздействия солнечного света одинаков для каждого уровня частоты полива.
То есть, поливают ли растение ежедневно или еженедельно, это не влияет на то, как воздействие солнечного света влияет на растение.
Дополнительные ресурсы
Следующие руководства предоставляют дополнительную информацию о моделях ANOVA:
Как интерпретировать F-значение и P-значение в ANOVA
Как рассчитать сумму квадратов в ANOVA
Что означает высокое значение F в ANOVA?