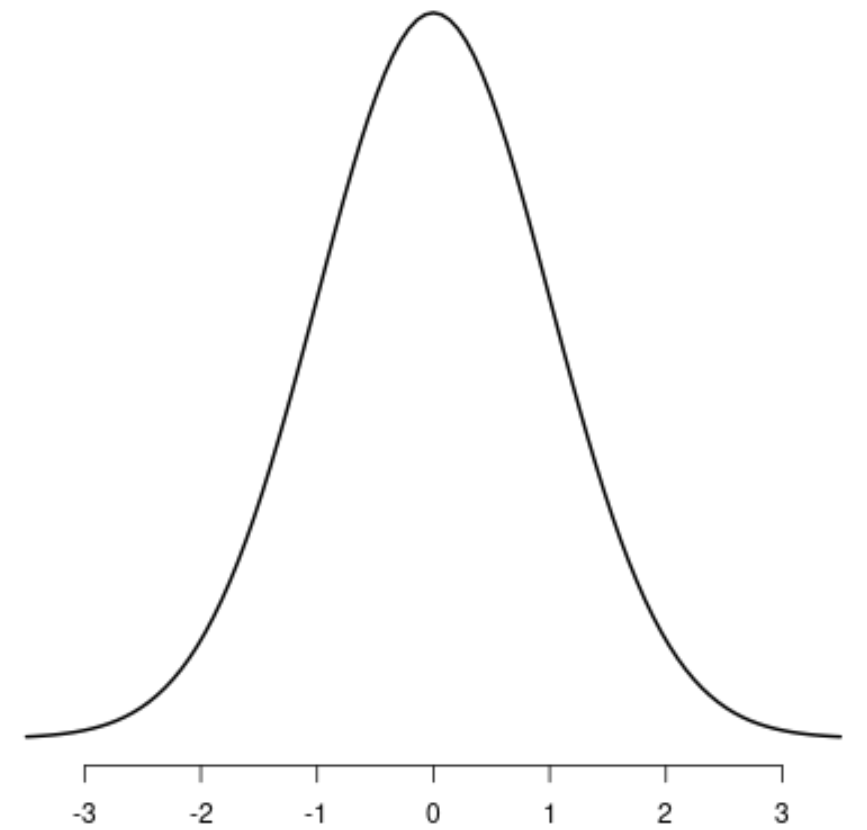
Нормальное распределение является наиболее часто используемым распределением вероятностей во всей статистике.
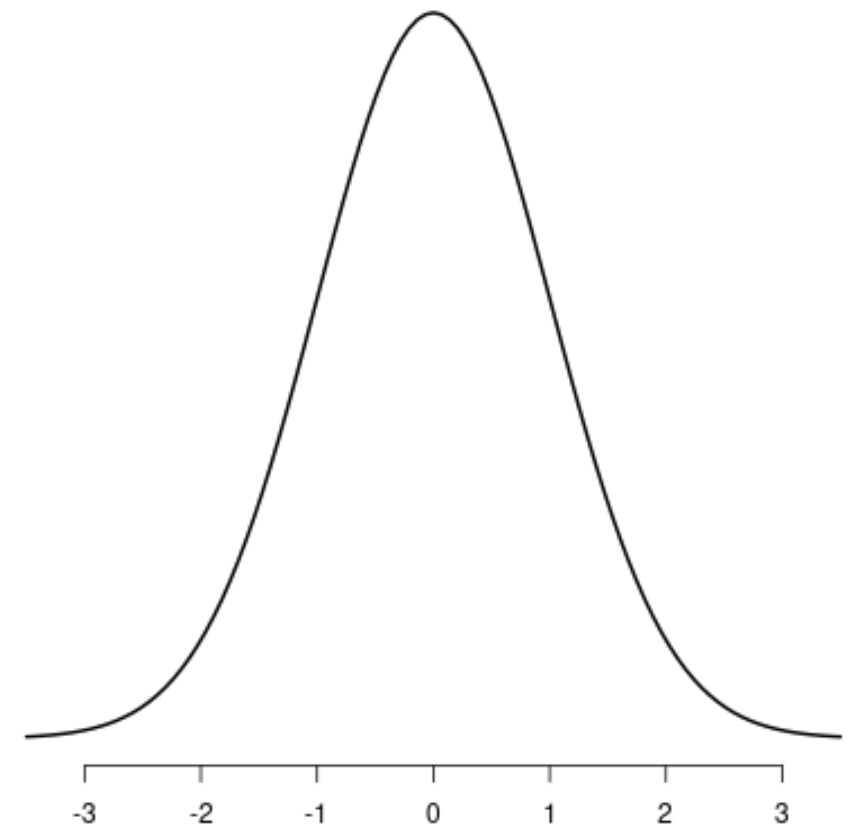
Он имеет следующие свойства:
- колоколообразный
- Симметричный
- Унимодальный – имеет одну «вершину».
- Среднее и медиана равны; оба расположены в центре распределения
- Около 68% данных находятся в пределах одного стандартного отклонения от среднего
- Около 95% данных находятся в пределах двух стандартных отклонений от среднего
- Около 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения.
В этом руководстве представлены 6 примеров реальных явлений, которые на самом деле следуют нормальному распределению.
Пример 1: Масса тела младенцев при рождении
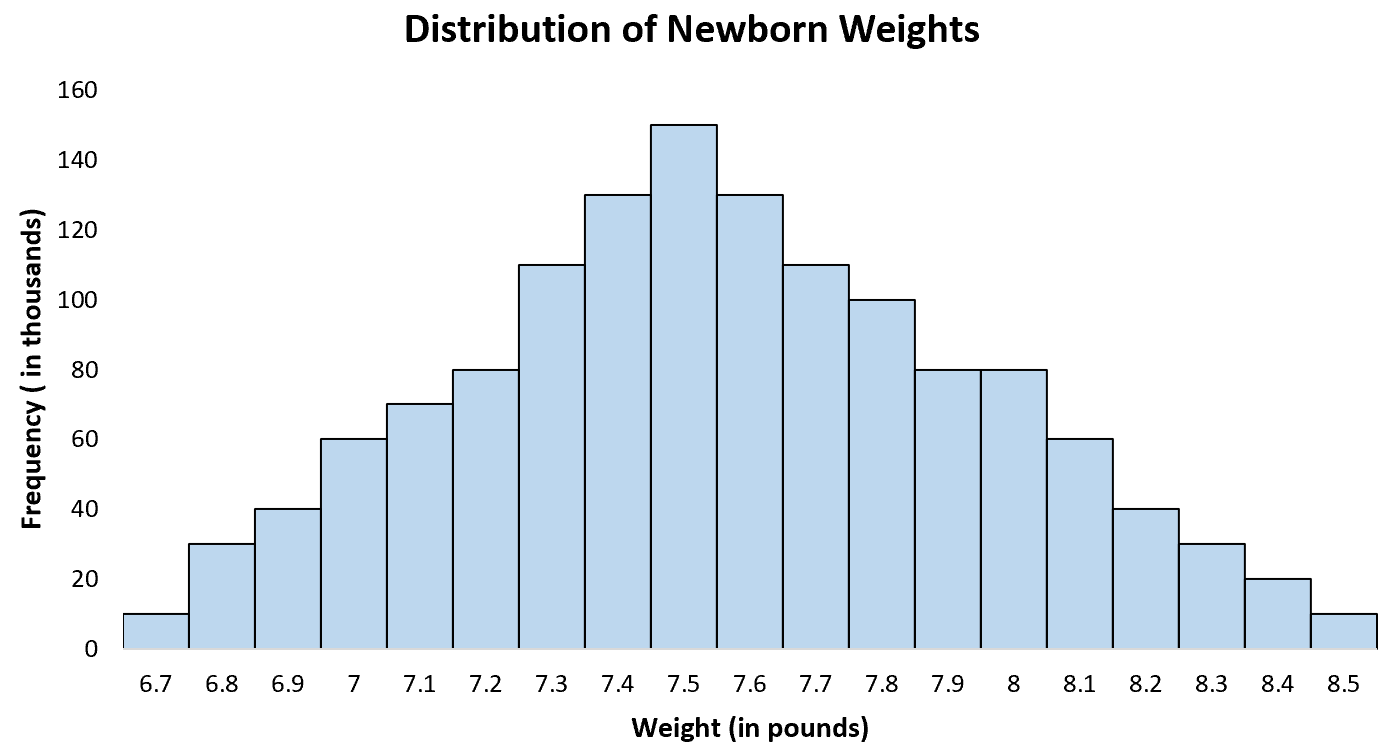
Хорошо задокументировано, что вес новорожденных при рождении обычно распределяется со средним значением около 7,5 фунтов.
Гистограмма массы тела при рождении новорожденных в США имеет колоколообразную форму, которая обычно имеет нормальное распределение:
Пример 2: Рост мужчин
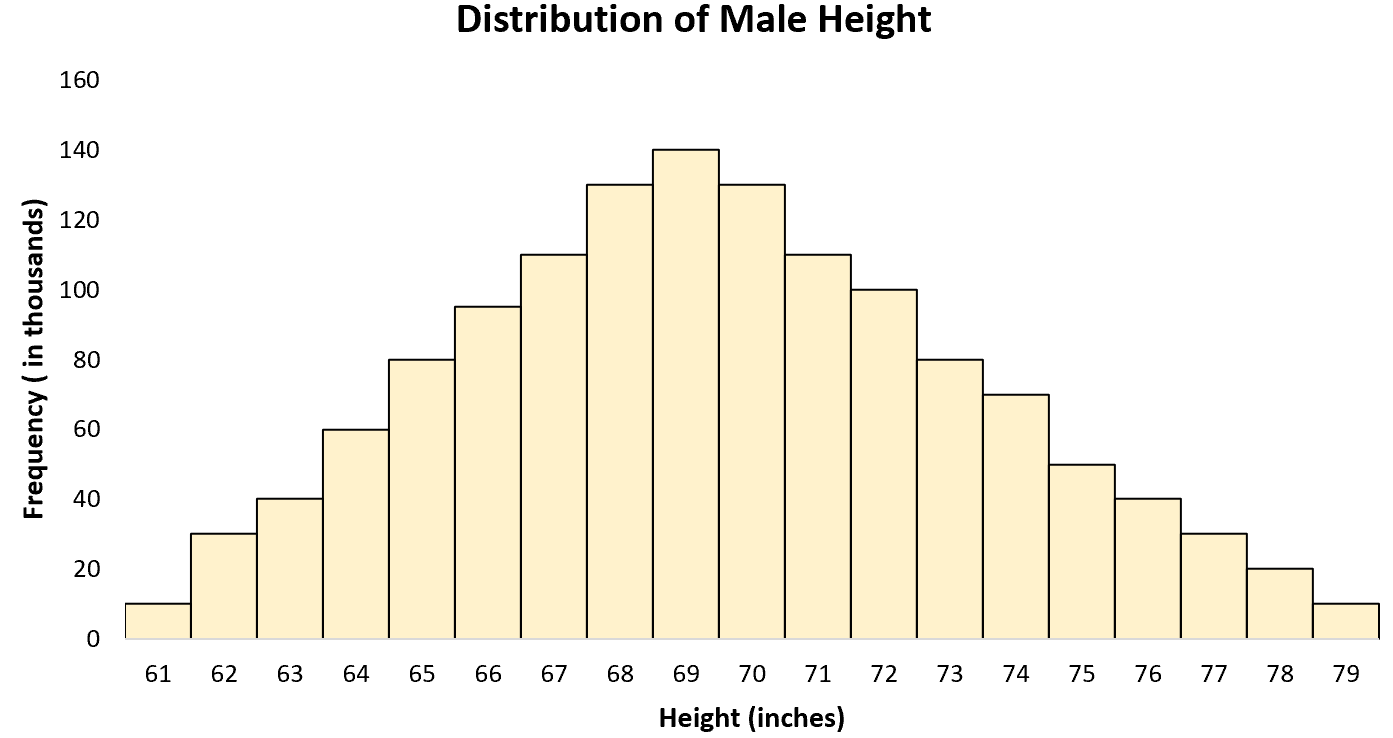
Распределение роста мужчин в США примерно нормальное со средним значением 70 дюймов и стандартным отклонением 3 дюйма.
Гистограмма роста всех мужчин США имеет форму колокола:
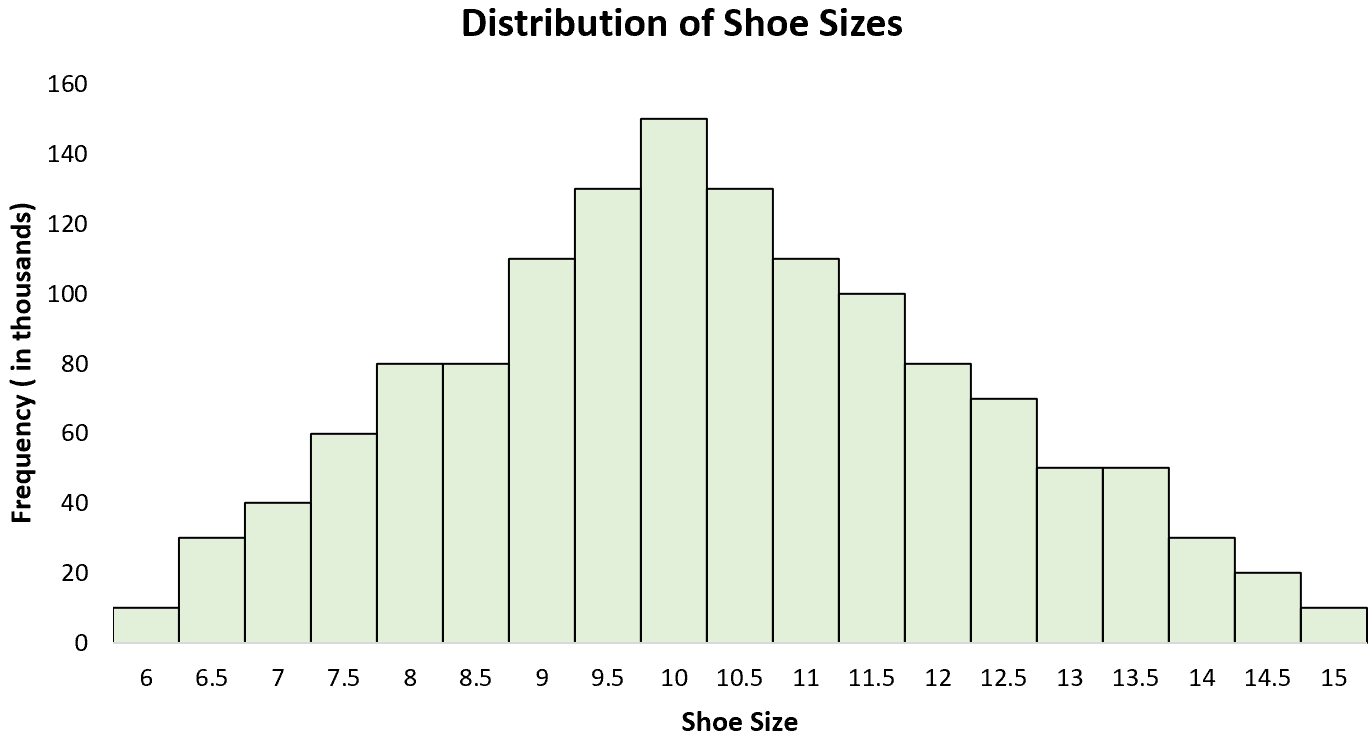
Пример 3: Размеры обуви
Распределение размеров обуви для мужчин в США примерно нормальное распределение со средним размером 10 и стандартным отклонением 1.
Гистограмма размеров обуви всех мужчин США показывает форму колокола с одним пиком в размере 10:
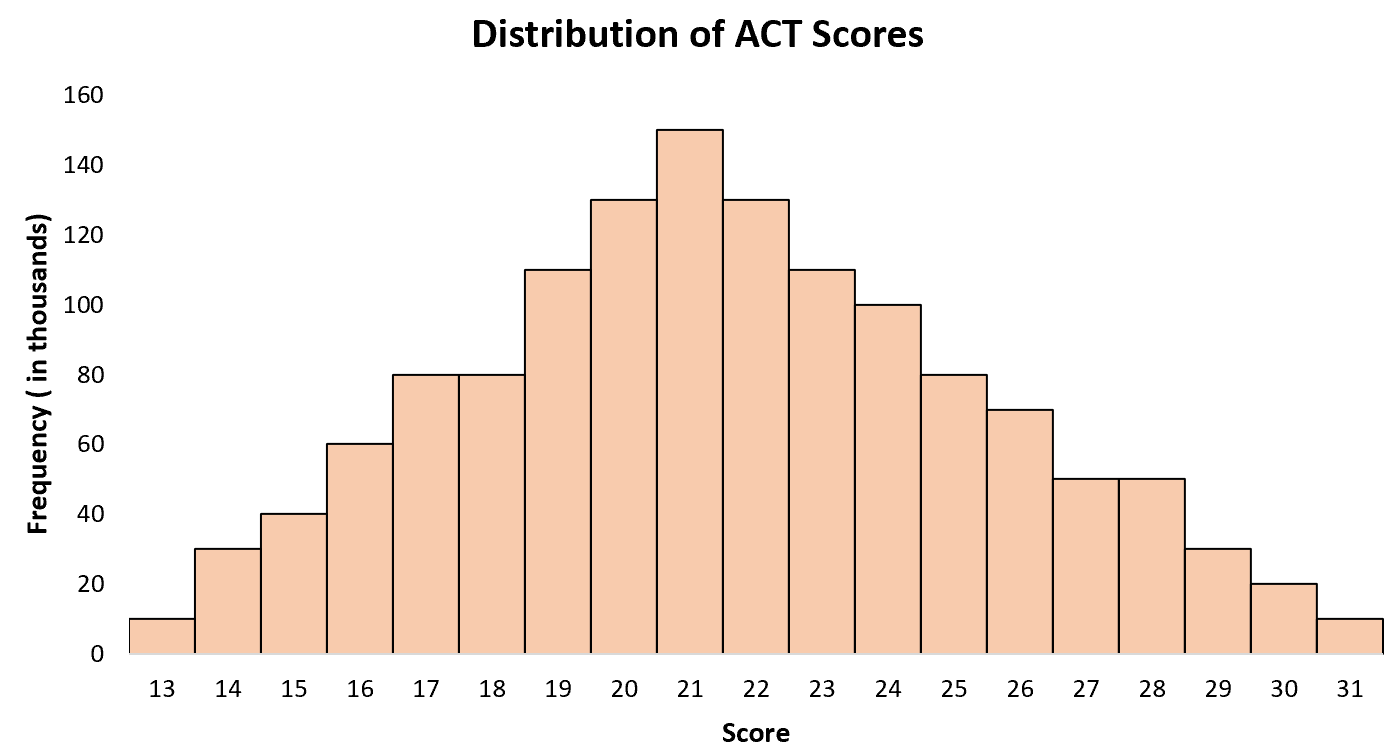
Пример 4: баллы ACT
Распределение баллов ACT для старшеклассников в США обычно распределяется со средним значением 21 и стандартным отклонением около 5.
Гистограмма результатов ACT для всех учащихся средних школ США иллюстрирует это нормальное распределение:
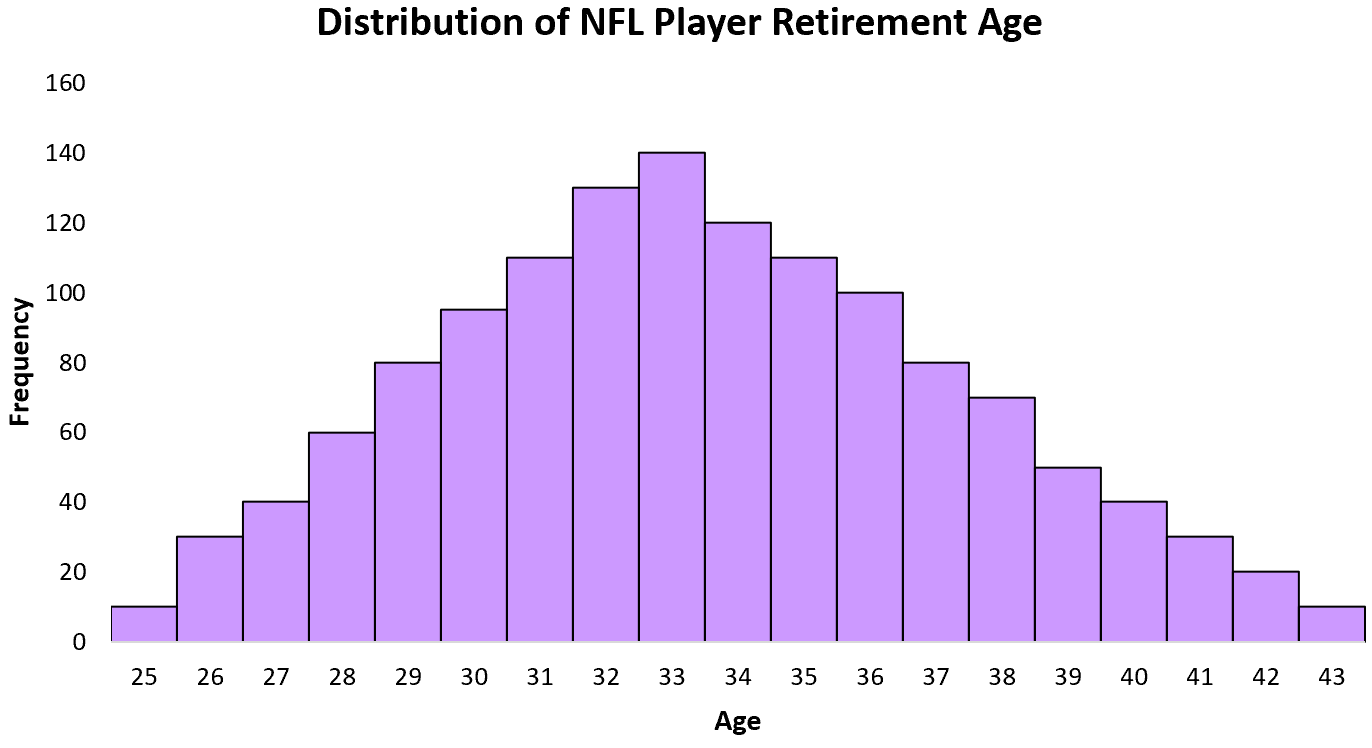
Пример 5: Средний пенсионный возраст игроков НФЛ
Распределение пенсионного возраста для игроков НФЛ обычно распределяется со средним значением 33 года и стандартным отклонением около 2 лет.
Гистограмма этого распределения имеет классический колоколообразный вид:
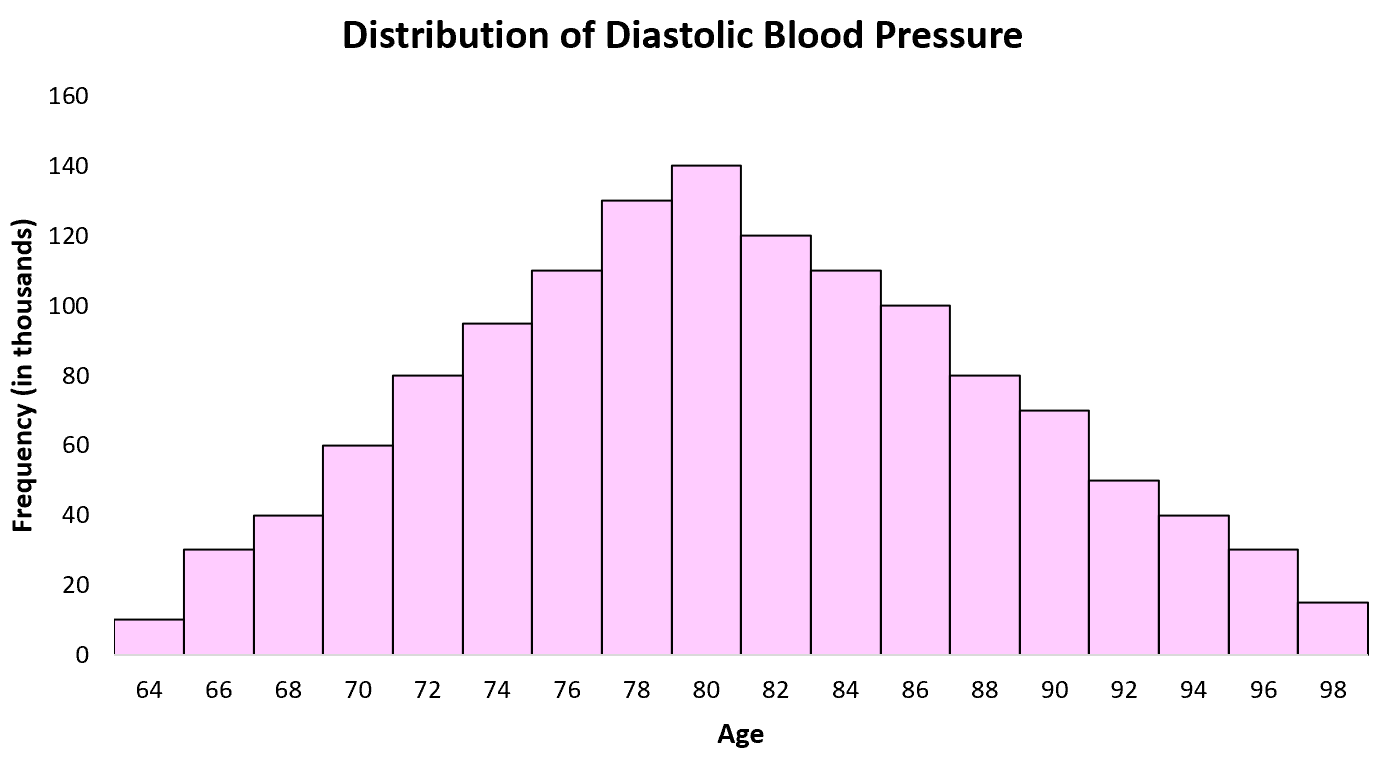
Пример 6: Артериальное давление
Распределение диастолического артериального давления у мужчин обычно распределяется со средним значением около 80 и стандартным отклонением 20.
Гистограмма распределения артериального давления для всех средних значений показывает нормальное распределение в форме колокола:
Дополнительные ресурсы
В следующих руководствах представлены примеры других распределений вероятностей в реальной жизни:
5 реальных примеров распределения Пуассона
5 реальных примеров биномиального распределения
5 реальных примеров геометрического распределения
5 реальных примеров равномерного распределения