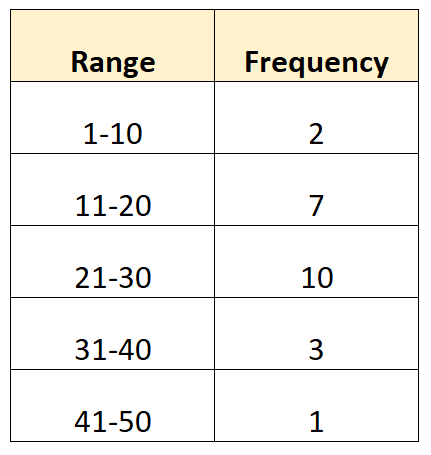
Часто нам может понадобиться вычислить среднее значение и стандартное отклонение данных, которые каким-то образом сгруппированы. Например, предположим, что у нас есть следующие сгруппированные данные:
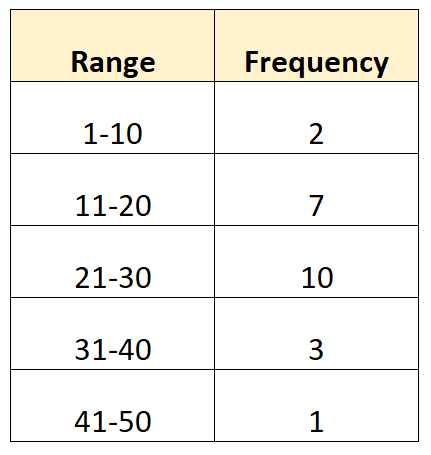
Хотя невозможно рассчитать точное среднее значение и стандартное отклонение, поскольку мы не знаем исходных значений данных , можно оценить среднее значение и стандартное отклонение.
Следующие шаги объясняют, как это сделать.
Связанный: Как найти режим сгруппированных данных
Вычислить среднее значение сгруппированных данных
Мы можем использовать следующую формулу для оценки среднего значения сгруппированных данных:
Среднее значение: Σm i n i / N
куда:
- m i : Середина i -й группы
- n i : Частота i -й группы
- N: общий размер выборки
Вот как мы могли бы применить эту формулу к нашему набору данных ранее:
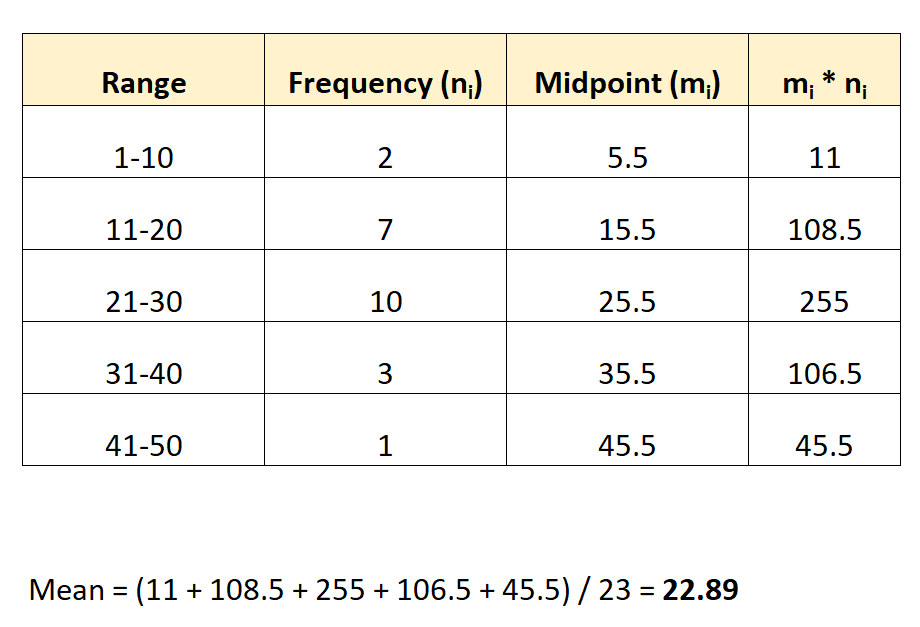
Среднее значение набора данных оказывается равным 22,89 .
Примечание. Среднюю точку для каждой группы можно найти, взяв среднее значение нижнего и верхнего значения диапазона. Например, средняя точка для первой группы рассчитывается как: (1+10)/2 = 5,5.
Вычислите стандартное отклонение сгруппированных данных
Мы можем использовать следующую формулу для оценки стандартного отклонения сгруппированных данных:
Стандартное отклонение: √ Σn i (m i -μ) 2 / (N-1)
куда:
- n i : Частота i -й группы
- m i : Середина i -й группы
- μ : среднее значение
- N: общий размер выборки
Вот как мы применим эту формулу к нашему набору данных:
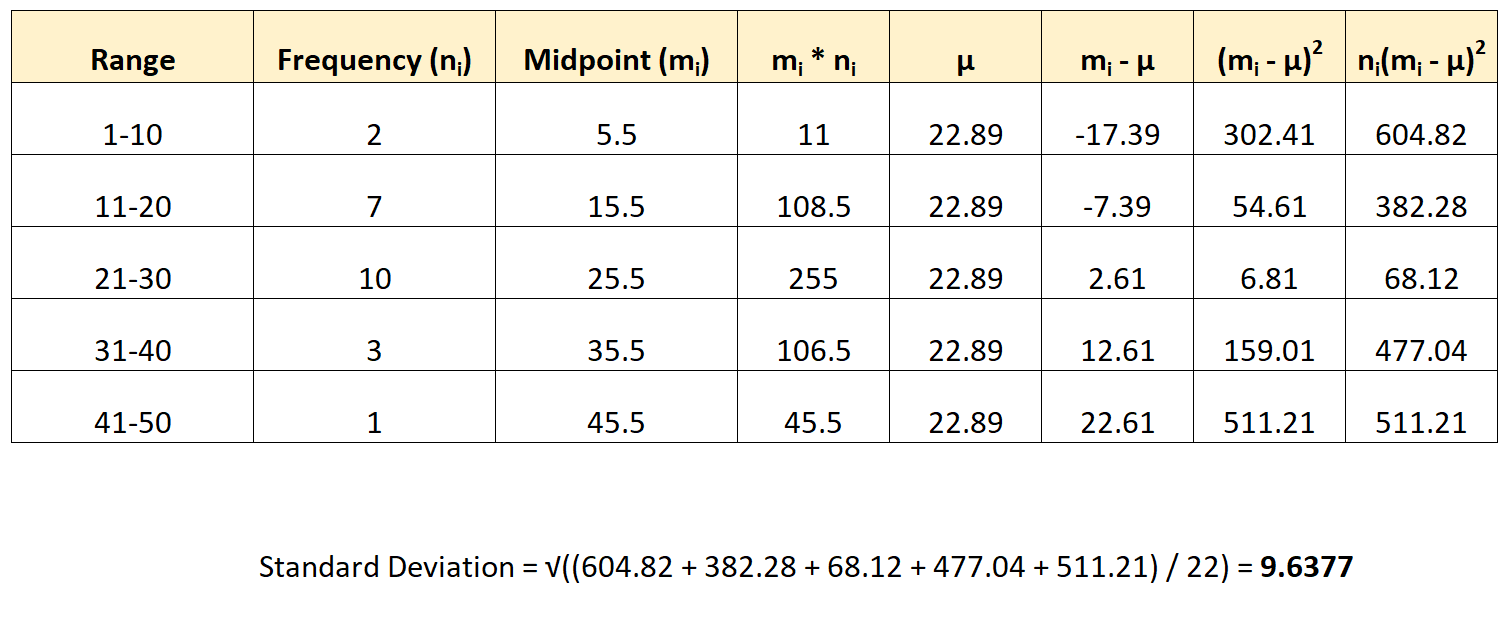
Стандартное отклонение набора данных оказывается равным 9,6377 .
Дополнительные ресурсы
Как оценить среднее значение и медиану любой гистограммы
Как рассчитать процентильный ранг для сгруппированных данных
Как найти медиану сгруппированных данных