Распределение Пуассона и нормальное распределение являются двумя наиболее часто используемыми распределениями вероятностей в статистике.
В этом руководстве дается краткое объяснение каждого дистрибутива, а также два основных различия между дистрибутивами.
Обзор: распределение Пуассона
Распределение Пуассона описывает вероятность получения k успехов за заданный интервал времени.
Если случайная величина X подчиняется распределению Пуассона, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = λk * e – λ / k !
куда:
- λ: среднее количество успехов за определенный интервал
- k: количество успехов
- e: константа, равная приблизительно 2,71828.
Например, предположим, что в конкретной больнице в среднем рождается 2 человека в час. Мы можем использовать приведенную выше формулу, чтобы определить вероятность 3 рождений в данный час:
P(X=3) = 2 3 * e – 2 / 3! = 0,1805
Вероятность рождения 3 детей в час равна 0,1805 .
Обзор: нормальное распределение
Нормальное распределение описывает вероятность того, что случайная величина примет значение в пределах заданного интервала.
Функция плотности вероятности нормального распределения может быть записана как:
P(X=x) = (1/σ√ 2π )e-1/2 ((x-μ)/σ) 2
куда:
- σ: стандартное отклонение распределения
- μ: среднее значение распределения
- x: значение для случайной величины
Например, предположим, что вес определенного вида выдр нормально распределен с μ = 40 фунтов и σ = 5 фунтов.
Если мы случайным образом выберем выдру из этой популяции, мы можем использовать следующую формулу, чтобы найти вероятность того, что она весит от 38 до 42 фунтов:
P(38 < X < 42) = (1/σ√ 2π )e -1/2((42-40)/5) 2 – (1/σ√ 2π )e -1/2((38-40) /5) 2 = 0,3108
Вероятность того, что случайно выбранная выдра весит от 38 до 42 фунтов, равна 0,3108 .
Отличие №1: дискретные и непрерывные данные
Первое различие между распределением Пуассона и нормальным распределением заключается в типе данных, которые моделирует каждое распределение вероятностей.
Распределение Пуассона используется, когда вы работаете с дискретными данными , которые могут принимать только целочисленные значения, равные или большие нуля. Вот некоторые примеры:
- Количество звонков, полученных в час в колл-центре
- Количество посетителей в день в ресторане
- Количество ДТП в месяц
В каждом сценарии случайная величина может принимать только значения 0, 1, 2, 3 и т. д.
Нормальное распределение используется, когда вы работаете с непрерывными данными , которые могут принимать любое значение от отрицательной бесконечности до положительной бесконечности. Вот некоторые примеры:
- Вес определенного животного
- Высота определенного растения
- Время марафона женщин
- Температура в градусах Цельсия
В этих сценариях случайные величины могут принимать любое значение, например -11,3, 21,343435, 85 и т. д.
Отличие № 2: Форма дистрибутивов
Второе различие между пуассоновским и нормальным распределением заключается в форме распределений.
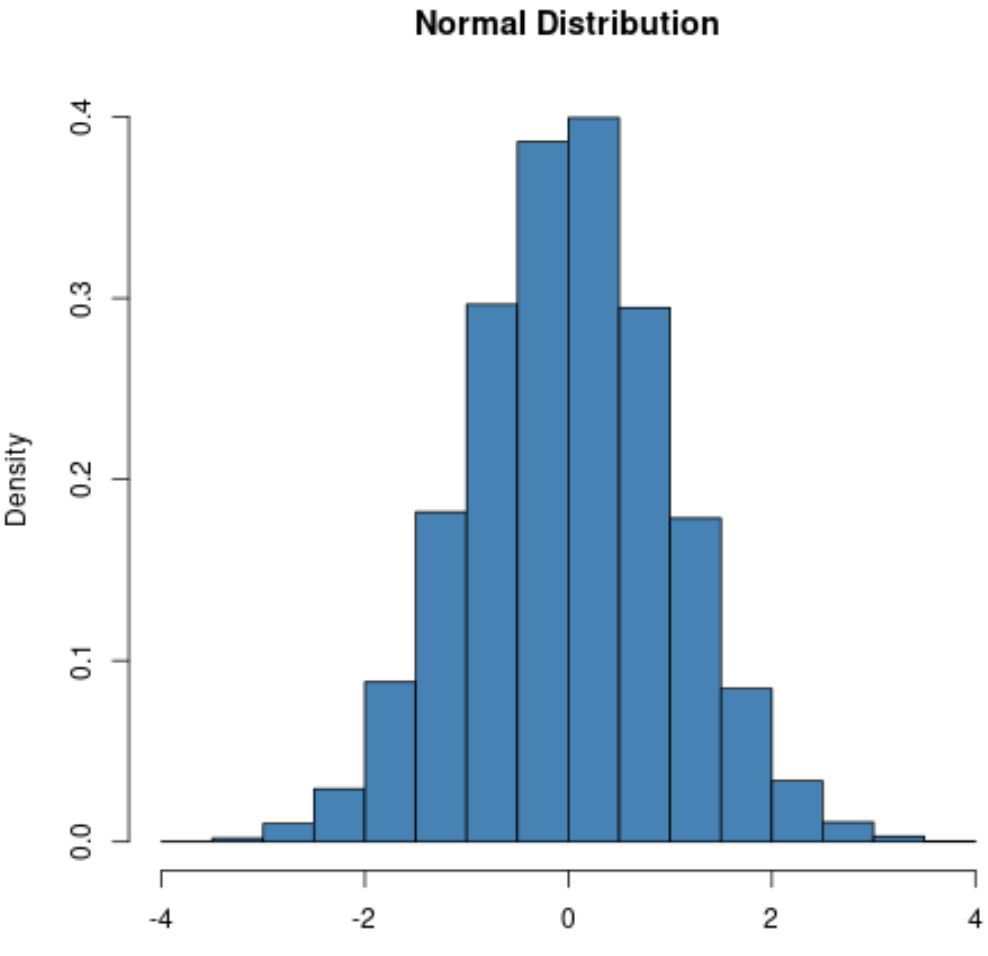
Нормальное распределение всегда имеет форму колокола:

Однако форма распределения Пуассона будет варьироваться в зависимости от среднего значения распределения.
Например, распределение Пуассона с небольшим значением среднего значения, например μ = 3 , будет сильно искажено вправо :

Однако распределение Пуассона с большим значением среднего, например μ = 20 , будет иметь колоколообразную форму, как и нормальное распределение:

Обратите внимание, что нижняя граница распределения Пуассона всегда будет равна нулю, независимо от значения среднего, потому что распределение Пуассона можно использовать только с целочисленными значениями, которые равны или больше нуля.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о распределении Пуассона:
Введение в распределение Пуассона
Четыре предположения о распределении Пуассона
5 реальных примеров распределения Пуассона
В следующих руководствах представлена дополнительная информация о нормальном распределении:
Введение в нормальное распределение
6 реальных примеров нормального распределения
Генератор набора данных нормального распределения