Повторные измерения ANOVA используются для определения того, существует ли статистически значимая разница между средними значениями трех или более групп, в которых одни и те же субъекты обнаруживаются в каждой группе.
Однако, прежде чем мы выполним повторные измерения ANOVA, мы должны убедиться, что выполняются следующие предположения:
1. Независимость: каждое из наблюдений должно быть независимым.
2. Нормальность: распределение переменной отклика нормально распределено.
3. Сферичность: дисперсии разностей между всеми комбинациями родственных групп должны быть равными.
Если одно или несколько из этих предположений нарушаются, то результаты повторных измерений ANOVA могут быть ненадежными.
В этой статье мы даем объяснение каждому допущению, как определить, выполняется ли допущение, и что делать, если допущение нарушается.
Предположение 1: Независимость
Повторные измерения ANOVA предполагают, что каждое наблюдение в вашем наборе данных не зависит от любого другого наблюдения.
Как определить, выполняется ли это предположение
Самый простой способ проверить это предположение — убедиться, что каждый индивидуум в наборе данных был случайно выбран из населения с использованием метода случайной выборки .
Если использовался метод случайной выборки, можно с уверенностью предположить, что каждое наблюдение является независимым.
Что делать, если это предположение нарушается
Если это допущение нарушается, то возникает серьезная проблема, поскольку ценности каждого человека могут быть каким-то образом связаны друг с другом.
Часто единственным средством в этом сценарии является набор людей для нового исследования с использованием метода случайной выборки.
Предположение 2: нормальность
Повторные измерения ANOVA предполагают, что распределение переменной отклика нормально распределено .
Как определить, выполняется ли это предположение
Есть два способа проверить, выполняется ли это предположение:
1. Создайте гистограмму или график QQ
Вы можете визуально проверить, является ли распределение переменной отклика примерно нормальным, создав гистограмму или график QQ.
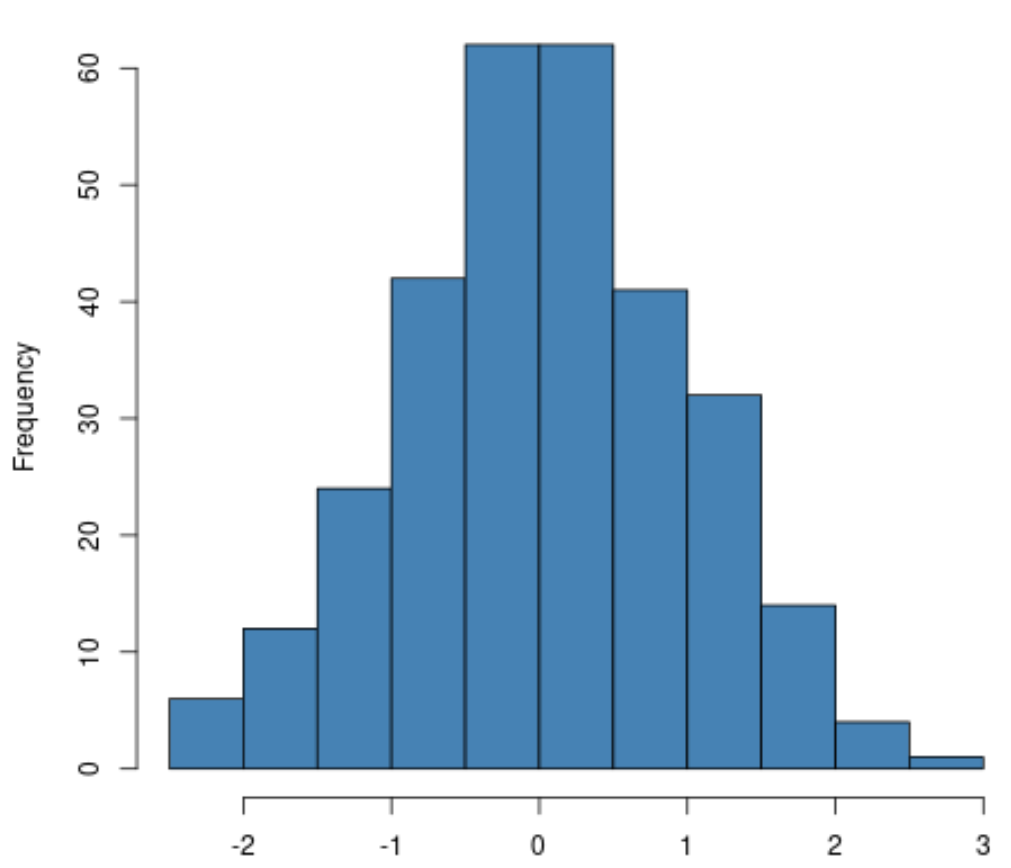
Если вы создаете гистограмму , просто убедитесь, что распределение переменной отклика примерно повторяет форму «колокола». Если это так, вы часто можете предположить, что предположение о нормальности выполнено:

Если вы создаете график QQ , проверьте, падают ли точки данных на прямую диагональную линию. Если да, то обычно можно предположить, что предположение о нормальности выполнено:

Связанный: Как использовать графики QQ для проверки нормальности
2. Проведите формальный статистический тест
Также можно провести тест Шапиро-Уилка на нормальность. Если p-значение теста меньше 0,05, это говорит о том, что данные не распределены нормально.
Однако имейте в виду, что при работе с чрезвычайно большими размерами выборки статистические тесты, такие как тест Шапиро-Уилка, почти всегда будут говорить вам, что ваши данные ненормальны.
По этой причине часто лучше проверять данные визуально, используя графики, такие как гистограммы и графики QQ. Просто взглянув на графики, вы можете получить довольно хорошее представление о том, нормально ли распределены данные.
Что делать, если это предположение нарушается
В целом, дисперсионный анализ с повторными измерениями считается достаточно устойчивым к нарушениям предположения о нормальности, если размеры выборки достаточно велики.
Если предположение о нормальности серьезно нарушено, у вас есть два варианта:
1. Преобразуйте значения отклика ваших данных, чтобы распределения были более нормально распределены.
2. Выполните эквивалентный непараметрический тест, такой как тест Фридмана , который не требует предположения о нормальности.
Допущение 3: сферичность
Повторные измерения ANOVA предполагают сферичность – дисперсии разностей между всеми комбинациями родственных групп должны быть равными.
Если это допущение нарушается, то F-отношение становится завышенным, а результаты повторных измерений ANOVA становятся ненадежными.
Как определить, выполняется ли это предположение
Чтобы проверить, выполняется ли это предположение, мы можем выполнить тест Мокли на сферичность .
В этом тесте используются следующие нулевая и альтернативная гипотезы:
- H 0 : Дисперсия разностей равна
- H A : Дисперсия разностей не равна
Если p-значение теста меньше некоторого уровня значимости (например, α = 0,05), то мы отклоняем нулевую гипотезу и делаем вывод, что дисперсии различий не равны.
В противном случае, если p-значение не меньше некоторого уровня значимости (например, α = 0,05), мы не можем отвергнуть нулевую гипотезу и сделать вывод, что предположение о сферичности выполнено.
В зависимости от того, какое статистическое программное обеспечение вы используете, результаты этого теста будут выглядеть примерно так:

Поскольку p-значение не меньше 0,05, мы не смогли бы отвергнуть нулевую гипотезу и сделать вывод, что предположение о сферичности выполняется в этом конкретном примере.
Что делать, если это предположение нарушается
Если мы отклоняем нулевую гипотезу теста Мочли на сферичность, то мы обычно применяем поправку к степеням свободы, используемым для расчета F-значения в таблице повторных измерений ANOVA.
Мы можем применить три поправки:
- Хьюн-Фельдт (наименее консервативный)
- Теплица-Гейссер
- Нижняя граница (наиболее консервативная)
Каждая из этих поправок имеет тенденцию увеличивать p-значения в выходной таблице повторных измерений ANOVA, чтобы учесть тот факт, что предположение о сферичности нарушается.
Затем мы можем использовать эти p-значения, чтобы определить, должны ли мы отклонить или не отклонить нулевую гипотезу повторных измерений ANOVA.
Дополнительные ресурсы
Следующие руководства предоставляют дополнительную информацию о повторных измерениях ANOVA:
Введение в повторные измерения ANOVA
Калькулятор повторных измерений ANOVA
Как сообщить о результатах дисперсионного анализа с повторными измерениями
Однофакторный дисперсионный анализ и дисперсионный анализ с повторными измерениями: разница